Файл: Направление подготовки 18. 03. 01 Химическая технология отчёт по лабораторной работе по дисциплине "Физика" Тема Изучение интерференции света от двух щелей. Дифракция Фраунгофера в лазерном излучении..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 158
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Пермский Национальный Исследовательский Политехнический Университет»
Факультет химических технологий, промышленной экологии и биотехнологий
Направление подготовки: 18.03.01 Химическая технология
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
По дисциплине: “Физика”
Тема:
«Изучение интерференции света от двух щелей.
Дифракция Фраунгофера в лазерном излучении.»
Работу выполнила:
студентка1-огокурса,группаХТ1-19-1б
Тверитина Александра Ивановна
Научный руководитель:
доцент,кандидатфизико-математическихнаук
Сабиров Рустам Рустямович
г. Пермь, 2020
Введение
Изучение интерференции света от двух щелей начнём с теоретического описания.
Интерференция – это явление сложения (суперпозиции) колебаний от нескольких источников когерентных волн. Рассмотрим два точечных когерентных источника S1 и S2. Колебания, от которых происходят с одинаковой частотой, а разность фаз колебаний равна нулю (источники синфазны). Пусть от источника S1 распространяются бегущие волны в среде 1 с показателем преломления n1, а от источника S2 – в среде 2 с показателем преломления n2 (рис. 1). На рисунке линия ОО1 – граница между этими прозрачными средами.
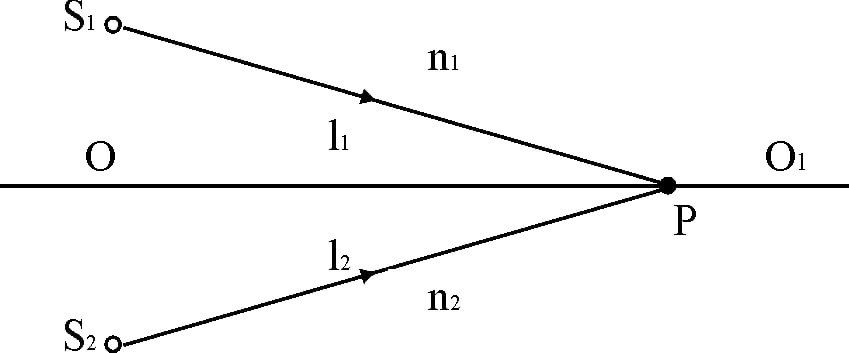 |
| Рис. 1. Интерференция (изображение взято из методического пособия «Изучение интерференции света от двух щелей»). |
На границе ОО1 выберем точку Р и определим условие минимума и максимума амплитуды результирующего колебания в этой точке пространства. Обозначим
l1=S1P, l2=S2P. Для электромагнитных волн (свет – электромагнитная волна) колебания вектора
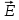 от двух одинаковых источников 1 и 2 определяются выражениями:
от двух одинаковых источников 1 и 2 определяются выражениями: 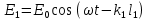 и
и 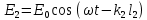 . E0 – амплитуда гармонических колебаний, k – волновое число.
. E0 – амплитуда гармонических колебаний, k – волновое число.В точке наблюдения Р происходит сложение колебаний одинаковой частоты. Будем считать, что эти колебания происходят вдоль одного направления. Разность фаз колебаний в этой точке равна
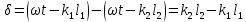 , (1)
, (1)где
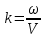 – волновое число;
– волновое число; 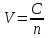 – скорость распространения электромагнитной волны в среде с показателем n, С – скорость волны в вакууме. Так как
– скорость распространения электромагнитной волны в среде с показателем n, С – скорость волны в вакууме. Так как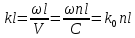 , (2)
, (2)где
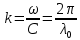 – волновое число для среды с n=1 (вакуум), λ0 – длина волны в среде с n=1, то разность фаз колебаний
– волновое число для среды с n=1 (вакуум), λ0 – длина волны в среде с n=1, то разность фаз колебаний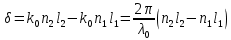 (3)
(3)Определяет результирующее колебание в точке Р.
Величина nl – оптический путь, разность этих величин для двух волн
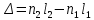 – оптическая разность хода, а
– оптическая разность хода, а 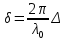 . Из условия минимума при сложении колебаний
. Из условия минимума при сложении колебаний 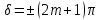 , m=0, 1, 2,…, получаем
, m=0, 1, 2,…, получаем 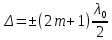 . Условие максимума для разности фаз –
. Условие максимума для разности фаз – 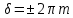 (колебания происходят в одной фазе) определяет условие максимума для оптической разности хода Δ:
(колебания происходят в одной фазе) определяет условие максимума для оптической разности хода Δ: 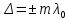 .
.
Можно сказать, что при сложении колебаний в любой точке пространства результирующее колебание определяется величиной оптической разности хода.
Методика эксперимента
Рассмотрим монохроматическую световую волну (длина волны в вакууме λ0) с плоским фронтом, падающую на непрозрачный экран с двумя узкими щелями (оптическая схема, близкая к схеме опыта Юнга). Пусть экран, где расположены узкие щели, может поворачиваться относительно точки О – середины расстояния d между источниками S1 и S2 (рис.2) на некоторый угол . В условиях эксперимента d=2b, где b – ширина щели. Можно показать, что распространение волн от щелей одинакового размера b с расстоянием между ними (ширина непрозрачного промежутка), равном этому же размеру b, при падении плоскопараллельного пучка света, происходит таким же образом, как и от двух точечных источников. Теорию таких двух точечных источников мы и рассмотрим ниже.
Экран наблюдения (обычный лист бумаги) располагается на расстоянии ОА=L, отсчитываемом от точки О, х – координата точки наблюдения Р равна расстоянию АР.
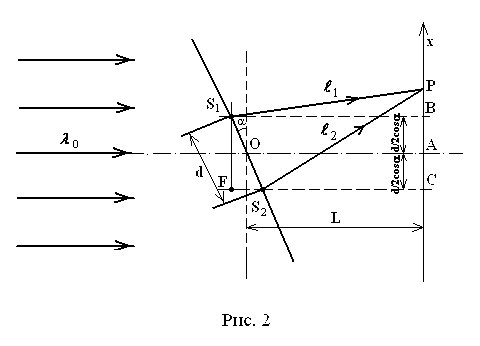 |
| Рис. 2. Оптическая схема, близкая к схеме опыта Юнга (изображение взято из методического пособия «Изучение интерференции света от двух щелей»). |
Оптическая разность хода лучей 1 и 2 от плоского фронта до щелей равна Δ1=FS2=dsinα, а оптическая разность хода лучей 1 и 2 после прохождения щелей S1 и S2 равна Δ
2 (n=1). На экран лучи 1 и 2 приходят с разностью хода Δ=Δ1+Δ2. Рассчитаем Δ2. Из прямоугольных треугольников S1BP и S2CP:
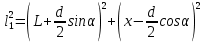 (4)
(4)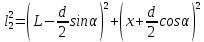 ,
, 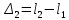 (5)
(5)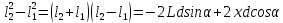 (6)
(6)При условии d<<L, l1≈l2≈L
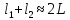 (7)
(7)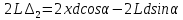 (8)
(8)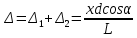 (9)
(9)Из условия максимума для интерферирующих лучей 1 и 2
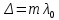 , где m=0, ±1, ±2, ±3,…, получим координаты точек экрана с максимальной интенсивностью света:
, где m=0, ±1, ±2, ±3,…, получим координаты точек экрана с максимальной интенсивностью света: 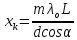 . Расстояние между ними равно
. Расстояние между ними равно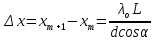 (10)
(10)Из (10) видно, что ширина интерференционной полосы не зависит от положения максимума и по её величине можно определить расстояние между щелями. Измеряя расстояние Δx между центрами соседних светлых полос, можно рассчитать
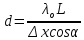 (11)
(11)Лабораторная работа позволит разобраться с понятием интерференции света. При изучении интерференции света от двух щелей у нас будет возможность увидеть в ходе эксперимента интерференционную картину.
Интерференционные методы представляют практическую ценность вследствие большой точности. Создание лазеров открывает новый этап в развитии оптики, примером может служить оптическая голография, получение трехмерного изображения, технологическое применение голографической интерферометрии. Интерференционный дилатометр наиболее точно определяет коэффициент линейного расширения тел.
Современные оптические устройства (объективы, фотоаппараты и др.) составлены из сравнительно большого количества линз, пластинок, зеркал. Поверхности частично отражают свет, так у линз - две отражающие поверхности. Во-первых, снижается интенсивность прошедшего света, во-вторых, плёнка в фотоаппарате частично засвечивается, вуалируется. Для устранения отражённого света линзу покрывают тонкой прозрачной плёнкой, такой, чтобы относительные показатели, преломления на границе воздух - пленка и границе пленка - стекло были одинаковыми в определённой области спектра. В результате интерференции волны взаимно уничтожаются, поверхность не отражает свет, поверхность окажется «просветлённой», так как все излучение, падающее на линзу, проходит через неё.
Благодаря интерференции мы имеем возможность видеть изображение предмета в натуральных цветах. Липпман получил цветную фотографию предмета без оптических систем, используя лишь интерференционный метод. От предмета в виде цветной стрелки лучи падают нормально на фотоэмульсию. В пучностях стоячих волн максимальное почернение образует прослойки, расстояние между которыми равно половине длины волны того цвета, который действовал на данное место пластины. Обработанную пластинку освещают под тем же углом белым светом. Свет отражается от каждой прослойки. Там, где расстояние между ними равно половине длины волны красного света λк/2, разность хода между волнами составит λк, для красных лучей выполняется условие интерференционного максимума. Для других длин волн в составе белого света условие максимума не выполняется. Когерентные волны, отраженные от прослоек, усиливают друг друга и в отраженном свете видим красный край предмета. Так же формируется изображение всех частей предмета включая фиолетовый край. Если освещать обработанную пластинку красным светом, то увидим изображение только красного края предмета.
Изучение дифракции Фраунгофера на одной щели, на одномерной и двумерной дифракционных решётках в монохроматическом свете лазерного источника начнём с теоретического описания.
Дифракцией называется круг явлений, связанных с огибанием волнами препятствий. Дифракция, как и интерференция, служит доказательством волновой природы света. Наиболее отчётливые дифракционные эффекты возникают при распространении света близ непрозрачных препятствий. Данное явление хорошо наблюдается, когда размеры препятствий соизмеримы с длиной волны, падающей на препятствие. Так как свет – это электромагнитная волна, длина волны которой составляет (0,4–0,7) мкм, то для наблюдения дифракции света размеры препятствий должны быть порядка микрометров.