Файл: Направление подготовки 18. 03. 01 Химическая технология отчёт по лабораторной работе по дисциплине "Физика" Тема Изучение интерференции света от двух щелей. Дифракция Фраунгофера в лазерном излучении..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 159
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
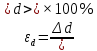 (34)
(34)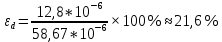
d = Δd ±
d = (59±13)*10-6 м
Отмечаем на листе бумаги положение чередующихся максимумов и минимумов интенсивности. Рассчитываем среднее расстояние между соседними максимумами интенсивности света по формуле (30). Рассчитываем по формуле (31) величины d (расстояние между щелями) для каждого из выбранных углов α. Полученные результаты вносим в таблицу №1. Затем определяем среднее значение величины d.
Исходя из данных, полученных в ходе лабораторной работы, можно сказать, что при увеличении угла падения увеличивается длина максимумов. Это происходит из-за того, что лучи света не одновременно достигают листа бумаги – это превращает их в более длинные полосы, и это отражается на значении d.
Чистый лист бумаги в клетку мы использовали во время эксперимента как экран наблюдения. Затем мы отметили на нём положение максимумов. Для удобства и точности измерений лист бумаги мы сфотографировали и открыли фотографию в Microsoft Office. Программа позволяет настроить масштаб фото таким образом, чтобы размер одной клеточки был равен 5 мм. Мы прикладывали линейку к экрану компьютера и проводили замеры (рис. 11).
 |
| Рис. 11. Измерение полученных максимумов. |
Дифракция Фраунгофера в лазерном излучении
 |
| Рис. 12. Дифракция Фраунгофера на одиночной щели. |
Таблица №2. Дифракция Фраунгофера на одиночной щели.
| Угол падения, град | Порядок спектра k | 2 xk,мм | xk, мм | b, мкм | <b>, мкм | Δb, мкм | ε, % |
| 0 | 1 | 25 | 12,5 | 28,9 | 29,9 | 3,33 | 11,1 |
| 2 | 40 | 20,0 | 30,1 | ||||
| 3 | 55 | 27,5 | 30,6 | ||||
| 30 | 1 | 27 | 13,5 | 26,7 | 26,7 | 0 | 0 |
| 2 | 25 | 22,5 | 26,7 | ||||
| 3 | 63 | 31,5 | 26,7 | ||||
| 60 | 1 | 43 | 21,5 | 16,78 | 16,28 | 1,76 | 10,8 |
| 2 | 75 | 37,5 | 16,03 | ||||
| 3 | 105 | 52,5 | 16,03 |
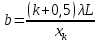 , (36)
, (36)где λ=0,65 мкм, L=370 мм.
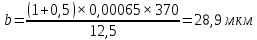
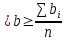 (37)
(37)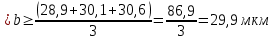
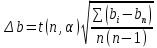 (38)
(38)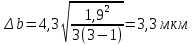
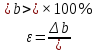 (39)
(39)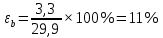
b = <b> ±Δb (40)
b = (30 ± 4) мкм
Отмечаем на листе бумаги положение центров главных максимумов первых трёх порядков. Миллиметровой линейкой измеряем расстояние 2xk между максимумами 1, 2 и 3-ого порядков по обе стороны от центрального максимума для углов падения Ɵ=0◦, 30◦ и 60◦. Полученные значения 2xk и xk вносим в таблицу №2. Затем вычисляем ширину щели b для каждого спектра k по формуле (36). Рассчитанные значения вносим в таблицу №2. После определяем среднее значение ширины решётки b. Рассчитываем абсолютную и относительную погрешность величины b. Результат вносим в таблицу №2.
При измерении порядка спектра, значение ширины одиночной щели уменьшается.
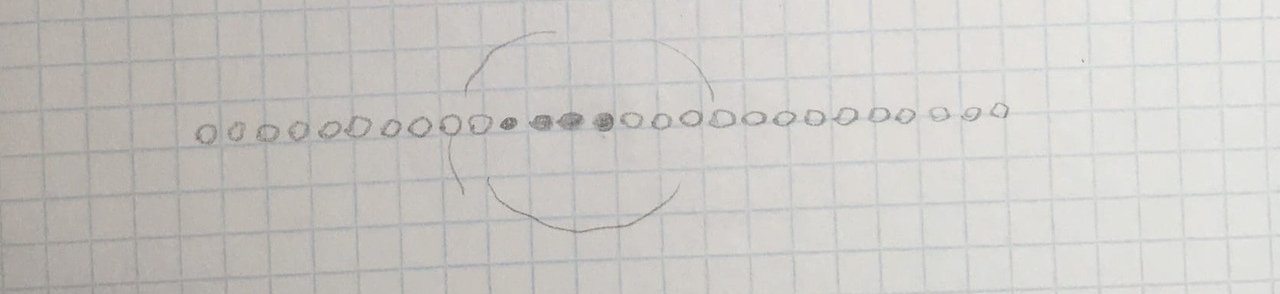 |
| Рис. 13. Дифракция на одномерной дифракционной решётке. |
Таблица №3. Дифракция на одномерной дифракционной решётке.
| Угол падения, град | Порядок спектра k | 2 xk,мм | xk, мм | d, мкм | <d>, мкм | Δd, мкм | ε, % |
| 0 | 1 | 7 | 3,5 | 68,7 | 68,57 | 0,9 | 1,3 |
| 2 | 14 | 7,0 | 68,4 | ||||
| 3 | 21 | 10,5 | 68,6 | ||||
| 30 | 1 | 9 | 4,5 | 63,3 | 63,5 | 1,12 | 1,76 |
| 2 | 17 | 8,5 | 64,1 | ||||
| 3 | 21 | 10,5 | 63,5 | ||||
| 60 | 1 | 12 | 6,0 | 40,1 | 41,3 | 7,7 | 18,6 |
| 2 | 22 | 11,0 | 40,1 | ||||
| 3 | 34 | 17,0 | 43,7 |
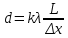 , при k=1, (41)
, при k=1, (41)где λ=0,65 мкм, L=370 мм
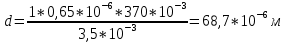
 (42)
(42)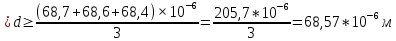
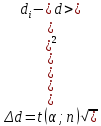 при α=0,95 (43)
при α=0,95 (43)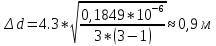
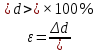 (44)
(44)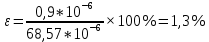
d= <d> ± Δd (45)
d= (69±1) мкм
Отмечаем на листе бумаги положение центров главных максимумов первых трёх порядков. Миллиметровой линейкой измеряем расстояние 2xk между максимумами 1, 2 и 3-ого порядков по обе стороны от центрального максимума для углов падения Ɵ=0◦, 30◦ и 60◦. Полученные значения 2xk и xk вносим в таблицу №3. Затем вычисляем постоянную дифракционной решётки d для каждого спектра k по формуле (41). Рассчитанные значения вносим в таблицу №3. После определяем среднее значение постоянной решётки d, рассчитываем абсолютную и относительную погрешность по методу косвенных невоспроизводимых измерений. Результат заносим в таблицу №3.
При вычисления постоянной дифракционной решётки значения сильно не расходились, что показывает достаточно точное указание точек на листе.
 |  | 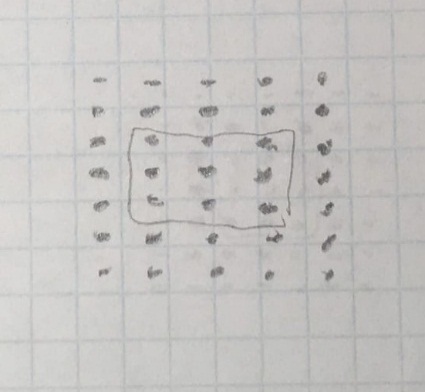 |
| 0◦ | 30◦ | 60◦ |
| Рис. 14. Дифракция на двумерной дифракционной решётке. | ||
Таблица №4. Дифракция на двумерной дифракционной решётке.
Вдоль оси Х.
| α, град | l1, мм | N | Δxi, мм | λ, мкм | L, мм | d1, мкм | <d1>, мкм |
| 0 | 8 | 3 | 4,0 | 0,65 | 370 | 60,1 | 50,2 |
| 30 | 9 | 3 | 4,5 | 0,65 | 370 | 53,4 | |
| 60 | 13 | 3 | 6,5 | 0,65 | 370 | 37,0 |
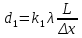 , приk=1(46)
, приk=1(46)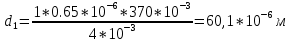
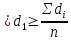 (47)
(47)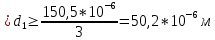
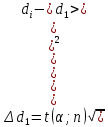 при α=0,95 (48)
при α=0,95 (48)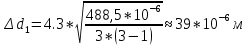
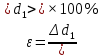 (49)
(49)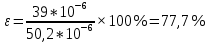
d1 = <d1>± Δd1 (50)
d1= (51±39) мкм
Вдоль оси У.
| α, град | l1, мм | N | Δуi, мм | λ, мкм | L, мм | d2, мкм | |
| 0 | 8 | 3 | 4,0 | 0,65 | 370 | 60,1 | 57,9 |
| 30 | 8 | 3 | 4,0 | 0,65 | 370 | 60,1 | |
| 60 | 9 | 3 | 4,5 | 0,65 | 370 | 53,4 |
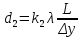 , при k2=1 (51)
, при k2=1 (51)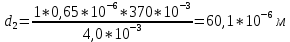
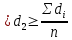 (52)
(52)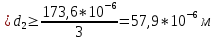
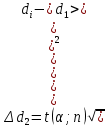 при α=0,95 (53)
при α=0,95 (53)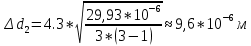
d2= Δd2 ± <d2> (54)
d2= (58±10)∙10-6
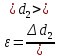 (55)
(55)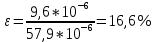
Отмечаем на листе бумаги положение симметрично расположенных относительно центра максимума световых пятен второго порядка вдоль оси X (k1, k2=2, 0; -2, 0) и Y (k1, k2=0, 2; 0, -2). Миллиметровой линейкой измеряем расстояние li между максимумами 2-ого порядка по обе стороны от центрального яркого пятна вдоль осей X, Y для углов падения Ɵ=0◦, 30◦ и 60◦. Полученные значения li в таблицу №4. Затем рассчитываем среднее расстояние между соседними максимумами интенсивности света по формуле (30), где N – число максимумов, укладывающихся на отмеренных расстояниях вдоль обеих осей. Определённые параметры вносим в таблицу №4. Вычисляем периоды дифракционной решётки d1, d2 для каждого угла падения по формулам: d1=k1λL/Δxi, d2=k2λL/Δyi, где k1=k2=1, λ=0,65 мкм, L=370 мм. После определяем среднее значение расстояния, рассчитываем абсолютную и относительную погрешность по методу косвенных невоспроизводимых измерений. Результат вносим в таблицу №4.
При увеличении угла падения картина дифракции растягивается вдоль оси Х, так как ход лучей идёт под углом вдоль оси Х. Это и приводит к увеличению расстояния между максимумами, что отражается на значении постоянной дифракционной решётки.
Анализ результатов
В ходе лабораторной работы мы значение расстояния между двумя щелями при интерференции света: d = (59±13) * 10-6 м (по формуле 35). При этом относительная погрешность равна 21,6% (по формуле 34).
В ходе лабораторной работы мы рассмотрели один из видов дифракции – дифракция Фраунгофера. С помощью дифракции Фраунгофера мы нашли постоянные дифракционных решёток.
Методика измерений дифракции Фраунгофера сопровождается систематическим изменением одного из параметров (порядок k дифракционного максимума), т.е. мы сталкиваемся со случаем косвенных измерений при невоспроизводимых условиях. Тогда значение косвенно измеряемой величины вычисляется для каждого отдельного измерения, а полученные результаты обрабатываются совместно, как прямые многократные измерения по методике Стьюдента при доверительной вероятности 0,95. Причём в косвенных измерениях при невоспроизводимых условиях учитываются только случайные погрешности.
В данной лабораторной работе был доказан принцип Гюйгенса-Френеля, который гласит: каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.
Доказательством данного принципа служит само понятие дифракции, и в опыте оно иллюстрируется в виде полученных максимумов.
При изучении дифракции Фраунгофера мы нашли несколько значений:
-
Ширина щели при дифракции на одиночной щели равна b = (30 ± 4) * 10-6 м (по формуле 40). При этом относительная погрешность равна 27,8% (по формуле 39). -
Постоянная одномерной дифракционной решетки равна d = (69 ± 1) * 10-6 м (по формуле 45). При этом относительная погрешность равна 1,3% (по формуле 44). -
Постоянная двумерной решётке равна: вдоль OX d1 = (51±39) * 10-6 (по формуле 50). При этом относительная погрешность равна 77,7% (по формуле 49). Вдоль OY d2 = (58±10) * 10-6 (по формуле 54). При этом относительная погрешность равна 16,6% (по формуле 55).
При этом значение d1 имеет большую погрешность, чем d2, так как угол падения луча шёл вдоль оси Х – это привело к увеличению расстояния между максимумами, что отражается на значении постоянной дифракционной решётки.
Дифракционная картина для одномерной дифракционной решётки – самый яркий центральный максимум наблюдается при ϕ = °0, симметрично относительно него расположены менее интенсивные главные максимумы высших порядков. Кроме главных минимумов, в некоторых направлениях возникают так называемые добавочные минимумы, что является следствием взаимной интерференции волн, идущих от каждой щели. Таким образом, в случае N щелей между двумя соседними главными максимумами располагается (N – 1) добавочных минимумов, разделенных добавочными максимумами, интенсивность которых очень мала и которые наблюдаются в направлении, удовлетворяющих условию – между двумя соседними главными максимумами располагается (N – 2) слабых по интенсивности добавочных максимумов. С ростом числа щелей N главные максимумы становятся все более резкими и яркими, а добавочные максимумы и минимумы практически сливаются в широкие темные промежутки между главными максимумами. Количество щелей определяет световой поток через решётку. Чем их больше, тем большая энергия переносится волной через неё.
Двумерная дифракционная решётка обычно имеет равные значения постоянной вдоль оси Х и вдоль оси Y. Из рисунка мы видим, что доверительный интервал постоянной дифракционной решетки вдоль оси Y входит в доверительный интервал постоянной дифракционной решетки вдоль оси Х, что доказывает, что наши расчёты верны.
Дифракционная картина для двумерной дифракционной решётки – чёткие, симметрично расположенные световые пятна, каждому из которых соответствует два целочисленных индекса k1 и k2.
Данная работа имеет большие погрешности, так как результаты опыта – штрихи на листе бумаги – зарисовывались от руки.
Заключение
В лабораторной работе по изучению дифракции Фраунгофера в лазерном излучении мы наблюдали типичную для дифракции на одиночной щели дифракционную картину: центральное яркое пятно, а по обеим сторонам от него чередующиеся максимумы и минимумы спадающей интенсивности. Дифракция Фраунгофера на одиночной щели объясняется принципом Гюйгенса-Френеля, согласно которому каждая точка щели является источником вторичных волн. Каждый такой источник излучает во всех направлениях (этим объясняется появление света в области геометрической тени). Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром.
При выполнении лабораторной работы была исследована интерференционная картина. Интерференционная картина представляет собой чередующиеся максимумы и минимумы интенсивности.
В ходе данной лабораторной работы мы ознакомились с такими понятиями как интерференция и дифракция света. Мы нашли значение расстояния между щелями в опыте с интерференцией, постоянные дифракционных решеток, ширину щели при дифракции. Интерференция и дифракция доказывают, что свет ведёт себя как волна.
Если фронт световой волны является плоским, то говорят о дифракции Фраунгофера, а если фронт волны сферический – то о дифракции Френеля. Большой интерес представляет собой случай дифракции Фраунгофера от бесконечно длинной щели (для этого достаточно, чтобы длина щели была значительно больше её ширины).
При падении плоской монохроматической волны на щель происходит дифракция света (огибание светом препятствия) в обе стороны от щели. В результате на экране, расположенном на расстоянии L от щели, наблюдается дифракционная картина в виде светлой центральной полосы с максимальной освещенностью и симметрично расположенных относительно центральной полосы светлых полос меньшей интенсивности, разделённых темными полосами. Интенсивность дифрагированного света от максимального до минимального значения уменьшается постепенно.
Углы φ, под которыми наблюдаются максимумы и минимумы освещенности, можно найти, используя метод зон Френеля. Для этого фронт волны, ограниченный щелью, надо разбить на отдельные участки (зоны Френеля) так, чтобы расстояние от краев соседних зон до 14 точки наблюдения отличалось на λ/2. Тогда волны от соседних зон будут приходить в точку наблюдения в противофазе и гасить друг друга. Если на фронте волны в щели окажется четное число зон, то под данным углом φ на экране будет наблюдаться минимум, а если нечетное – то максимум.
В ходе лабораторной работы мы столкнулись с такими погрешностями:
-
Методическая (методика измерений дифракции Фраунгофера сопровождается систематическим изменением одного из параметров); -
инструментальная (погрешность, связанная с точностью показаний приборов); -
систематическая (погрешность, связанная с измерениями – при произведении замеров были нанесены значения приблизительными чертами, затем измерения проводились по фото – человеческий фактор).
В ходе лабораторной работы также были встречены следующие понятия:
-
Зоны Френеля – это участки, на которые можно разбить поверхность световой волны для вычисления результатов дифракции света. -
Расходимость лазерного излучения – это угловая расходимость плоского или телесного угла, характеризующая ширину диаграммы направленности в дальней зоне по заданному уровню углового распределения энергии по отношению к её максимальному значению. Малая расходимость пучка света, излучаемого лазером, позволяет технически легко решать задачу фокусировки пучка в заданной точке исследуемой области двухфазной системы. -
Когерентность – этосогласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Когерентность означает способность света проявлять интерференционные эффекты. -
Монохроматические волны – это неограниченные в пространстве волны одной определенной и строго постоянной частоты. Так как ни один реальный источник не дает строго монохроматического света, то волны, излучаемые любыми независимыми источниками света, всегда некогерентны. -
Монохроматический свет – это световые колебания одной частоты. -
Интенсивность – это скалярная физическая величина, количественно характеризующая мощность, переносимую волной в направлении распространения. Численно интенсивность равна усреднённой за период колебаний волны мощности излучения, проходящей через единичную площадку, расположенную перпендикулярно направлению распространения энергии. -
Интерференция – это взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. -
Дифракция – это огибание светом встреченных на пути препятствий. -
Дифракция Фраунгофера случай дифракции, при которой дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка {\displaystyle {\frac {\rho ^{2}}{z\lambda }}}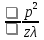 , что сильно упрощает теоретическое рассмотрение явления. Здесь z - расстояние от отверстия или преграды до плоскости наблюдения, λ -длина волны излучения, а p - радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат.
, что сильно упрощает теоретическое рассмотрение явления. Здесь z - расстояние от отверстия или преграды до плоскости наблюдения, λ -длина волны излучения, а p - радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. -
Дифракционная решётка – это оптический прибор, действие которого основано на использовании явления дифракции света. Представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. -
Постоянная дифракционной решётки – это ширина прозрачного штриха.