Различают два случая дифракции. Если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствие и лучи, идущие в точку наблюдения, образуют практически параллельные пучки, говорят о дифракции Фраунгофера или о дифракции в параллельных пучках. В противном случае говорят о дифракции Френеля или о дифракции в сходящихся пучках. Дифракционную картину Френеля достаточно просто объяснить на основе метода зон Френеля. Особый интерес представляет случай дифракции Фраунгофера от бесконечно длинной щели (для это достаточно, чтобы длина щели была значительно больше её ширины).

Для изучения дифракции Фраунгофера в качестве источника света удобно использовать лазер. Лазерное излучение отличается малой расходимостью, высокой когерентностью, высокой степенью монохроматичности и значительной интенсивностью. В этом случае отпадает необходимость в линзах. Лазерный пучок направляется на преграду, а дифрагированные в различных направлениях волны дают дифракционную картину, наблюдаемую на экране, расположенном на значительном расстоянии от препятствия.

На практике часто дифракционную картину Фраунгофера наблюдают на экране при помощи линзы, устанавливаемой перед экраном так, что он находится в её фокальной плоскости. Количественный расчёт дифракционной картины Фраунгофера значительно проще расчёта картины Френеля.

Дифракция Фраунгофера от узкой бесконечной щели

Пусть на длинную прямоугольную щель ширины b падает по нормали к ней плоская световая волна (рис. 3). Согласно принципу Гюйгенса-Френеля, элементарные участки открытой части волновой поверхности являются источниками вторичных цилиндрических волн. Поместим за щелью собирающую линзу, а в её фокальной плоскости – экран параллельный фронту падающей волны. Таким образом, речь идёт о волнах, распространяющихся параллельно. Условия для дифракции возникают после того, как линза фокусирует различные лучи в одной точке.

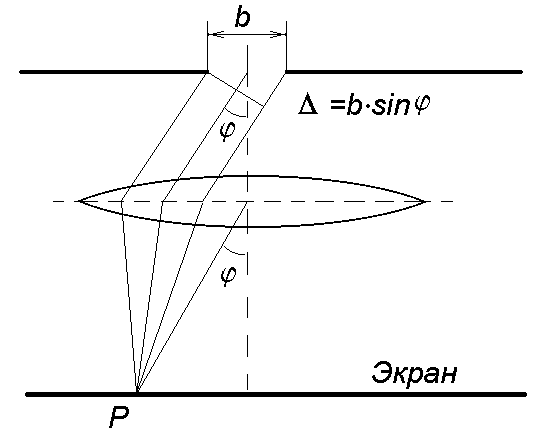Рис. 3. Дифракция света для одной щели (изображение взято из методического пособия «Дифракция Фраунгофера в лазерном излучении»).

Для описания картины, возникающей на экране, можно использовать разбиение щели на зоны Френеля. Однако здесь мы будем исходить из общих принципов дифракции – из интеграла Френеля. Рассмотрим рис. 3, где свет проходит через зазор шириной

---

bв непрозрачном препятствии. Волна, выходящая из щели под углом ϕ к центральной линии, имеет амплитуду (E₀/ b) dx, где величинаE₀определяется мощностью первичного источника света.

Волна, идущая от полоски с произвольной координатой 0<x<b, отличается от той волны, что исходит из точки x=0 разностью хода xsinϕ, а созданная этим дополнительная фаза естьkxsinϕ, гдеk=2π/λ – волновое число.Тогда результат действий всех парциальных волн, выходящих из щели ширинойbпод угломϕ и собранных линзой в точке Р, выражается формулой

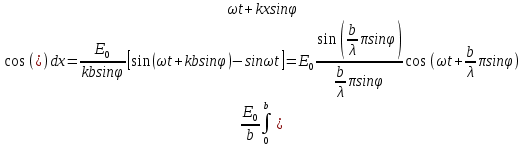(1)

Откуда видно, что амплитуда световой волны в точке Р есть

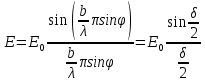, (2)

где

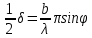
Освещённость (интенсивность света) в этой точке равна

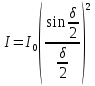, (12)

гдеI₀– интенсивность света в направлении падающей волны.

Как видно из формулы (12), при ϕ=0 освещённость максимальна, поскольку в пределе (sinδ)/δ=1 и I=I₀. В точках δ=±mπ, где m=1,2,3…, интенсивность обращается в нуль, то есть имеется минимум. Это условие можно записать как

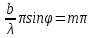или 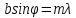m=1,2,3… (13)

Для некоторых первых максимумов с хорошей точностью можно считать, что максимумы располагаются ровно посередине между минимумами, и тогда условие максимумов может быть записано в виде

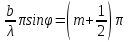
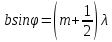(14)

При больших расстояниях L от решётки до экрана, суперпозиция параллельных дифрагированных лучей осуществляется на экране и без собирающей линзы.

Дифракция от дифракционной решётки

Дифракционной решёткой называется оптический прибор, состоящий из большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей или отражателей. Дифракционные решётки изготавливают из стекла или металла, на материале с помощью делительной машины через строго определённые расстояния наносятся параллельные штрихи. Стеклянные решётки предназначены для работы в проходящем свете, а металлические – в отражённом.

---

Период решётки – это расстояние d между серединами соседних щелей.

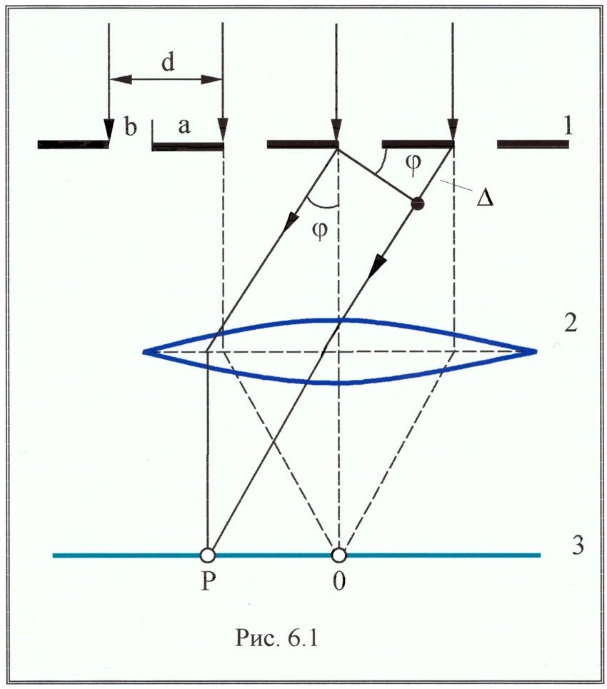Рис. 4. Дифракционная решётка, пропускающая свет (изображение взято с сайта https://www.учебнаятехника.рф/wps/izuchenie-difrakcii-sveta-fpv-5-3-3/).

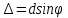
Световая картинка от дифракционной решётки – это наложение (суперпозиция) волновых фронтов, каждый из которых испытывает дифракцию Фраунгофера. Чтобы обеспечить условия для интерференции параллельных пучков, расположим параллельно решётке собирающую линзу, в фокальной плоскости которой поместим экран для наблюдения.

Пусть на решётку по нормали к ней падает плоская монохроматическая волна. Разность хода между вторичными волнами, испускаемыми любыми двумя соседними щелями, составляет dsinϕ, а разность фаз δ=kdsinϕ=(2dπ/λ)sinϕ. Обозначим через E₁ поле, создаваемое в точке Р первой щелью. Согласно формуле (1), его можно представить в виде

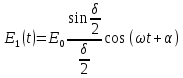(15)

Амплитуды полей, создаваемых остальными щелями

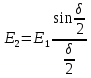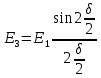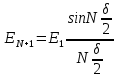, … (16)

Ряд (16) выражает поле, создаваемое дифракционной решёткой с числом щелей N под углом наблюденияϕ. Результатом такой N– лучевой интерференции является поле с амплитудой и интенсивностью

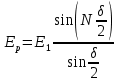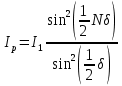, (17)

Поле от дифракционной решётки представляет собой поле от одиночной щели, умноженное на коэффициент, зависящий от числа щелей. Соответственно, интенсивность в точке наблюдения Р

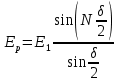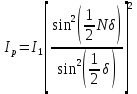, (18)

Формулы (17) и (18) являются основными в теории дифракционной решётки.

Точный вид угловой зависимости I_p(ϕ), задаваемой функцией (17), весьма сложен и представляет собой набор максимумов и минимумов различной высоты. Однако среди всех максимумов легко выделить последовательность главных, имеющих наибольшую величину освещённости. Для этого заметим, что главные дифракционные максимумы будут наблюдаться при таких углах ϕ, для которых волны, приходящие от всех щелей, находятся на одинаковой фазе. В таком максимуме разность фаз волн, пришедших от соседних щелей составляет

---

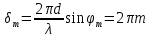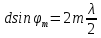, , m=0, ±1, ±2, …, (19)

где m– порядок дифракционного максимума.

Содержанием лабораторной работы является проверка простых условий: (13) для дифракции Фраунгофера (одна щель) и (19) для дифракционной решётки (N щелей).

Наклонное падание лучей на дифракционную решётку

Если плоская монохроматическая волна падает на решётку, работающую на пропускание, под углом Ɵ (рис. 5), тогда разность хода двух соседних лучей, дифрагировавших под углом ϕ равна:

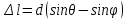(20)

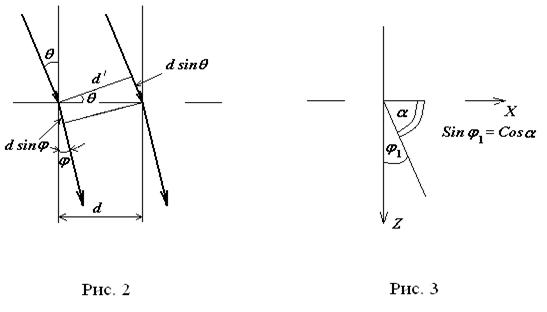Рис. 5. Дифракционная решётка, работающая на пропускание (изображение взято из методического пособия «Дифракция Фраунгофера в лазерном излучении»).

В этом случае (19), при котором наблюдаются главные максимумы интенсивности света, для дифракционной решётки запишется в виде:

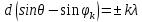(21)

где k=0, 1, 2, 3… - порядок главного максимума.

Распределение интенсивности дифрагированного света для решётки, состоящей из N элементов с шириной щели b и периодом решётки dв случае падения на неё излучения под углом Ɵ, будет иметь вид:

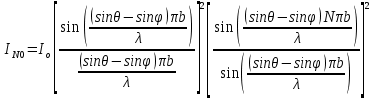, (22)

где I₀ – интенсивность не дифрагированного излучения (ϕ=0).

При d>>λуглы дифракции малы, т. е. ϕ_k≈Ɵ, и условие главных максимумов (21) можно переписать в виде:

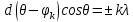, (23)

где k=0, 1, 2, 3…

При малых углах дифракции ϕ_k условие максимумов для нормального падения света на дифракционную решётку (19) можно переписать в виде:

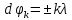, (24)

Сравнение (23) и (24) показывает, что угол дифракции (Ɵ-ϕ_k) при наклонном падении вычисляется так же, как и при нормальном падении света, но с уменьшением значения периода решётки d’=dcosƟ (кажущаяся постоянная решётки).

Следовательно, при большом наклоне падающего луча (Ɵ=90◦) кажущаяся постоянная решётки d’=dcosƟ становится весьма малой, и разрешающая способность решётки резко увеличивается. Это обстоятельство используется в исследовании кристаллических тел рентгеновскими лучами.

---

При изучении дифракции на одномерной дифракционной решётке можно заметить, что угол дифракции пропорционален длине волны λ. Дифракционная решётка разлагает белый свет на составляющие, причём отклоняет свет с большей длиной волны (красный) на больший угол (в отличие от призмы, где все происходит наоборот). Это свойство дифракционных решёток используется для определения спектрального состава света (дифракционные спектрографы, спектроскопы, спектрометры).

Дифракция на двумерной решётке

Двумерная решётка представляет собой скрещенные перпендикулярно друг другу решётки с периодами d₁ и d₂, причём часто d₁=d₂. Пусть ось X перпендикулярна щелям первой решётки. Ось Y – щелям второй, а ось Z направлена перпендикулярно плоскости двумерной решётки. Углы между падающими и дифрагированными лучами и осями X, Y, Z обозначим, соответственно, через α₀, β₀, γ₀ и α, β, γ. Очевидно, что α, β, γ – углы, дополняющие углы дифракции до 90◦ (рис. 6). Пусть на двумерную решётку нормально 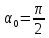, , 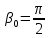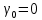падает плоская волна. Тогда условия возникновения главных максимумов для излучения с длиной волны λ имеют вид:

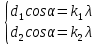, (25)

Углы α, β, γ связаны между собой соотношением

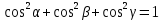, k=0, 1, 2, 3… (26)

Рис. 6. α, β, γ – углы, дополняющие углы дифракции до 90◦ (изображение взято из методического пособия «Дифракция Фраунгофера в лазерном излучении»).

Выражения (25) и (26) позволяют при известных d₁, d₂, λ определить углы α, β, γ, характеризующие направление дифрагированного луча для максимумов того или иного порядков. Если в каждой решётке число щелейN₁и N₂достаточно велико, то максимумы будут очень острыми и в них сосредоточится практически вся световая энергия дифрагировавших волн. В результате на экране, расположенном за двумерной решёткой получится дифракционная картина в виде чётких, симметрично расположенных световых пятен, каждому из которых соответствует два численных индекса

---

Смотрите также файлы

• Составила и провела классный руководитель 4 Д класса 20222023уч год классный час Стремление к знаниям, трудолюбие и патриотизм.docx

• Вы зашли под именем Митрофанова Анна Дмитриевна (Выход) анпоо "нспк".pdf

• Футбол. История создания великой игры.doc

• Реферат организация государственной статистики в Российской Федерации Выполнил Тошпулатов Достон Рахмонжон угли.docx

• Инструкция по выполнению практической работы выберите класс, тему урока в соответствии с прп и заполните представленную ниже таблицу..docx