ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Тульский государственный университет»
КОНТРОЛЬНА РАБОТА
по дисциплине
«Математика»
на тему
«Вариант № 1»
Выполнила студентка гр. № ИБ560221
интернет института Д.Д. Самолетова
Проверил: Д.В. Христич
канд. физ.-мат. наук, доц.
г. Тула, 2023
В задачах 21—30 даны координаты точек А, В, С. Требуется: 1) записать АВ и АС в системе орт и найти модули этих векторов; 2) найти угол между векторами АВ и АС ; 3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору АВ .
21. А(7; -4; 1), В(12; -3; 1), С(10; 1; 5).
Решение:
1) записать
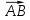и 
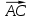в системе орт и найти модули этих векторов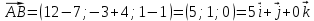
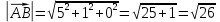
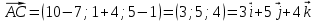
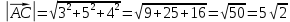
2) найти угол между векторам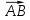и
и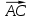 
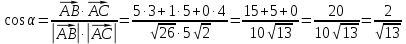
3) составить уравнение плоскости, проходящей через точку С перпендикулярно вектору
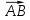.Уравнение плоскости в общем виде:
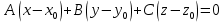
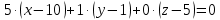
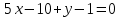
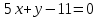
В задачах 31—40 даны векторы
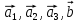. Показать, что векторы 
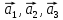образуют базис трехмерного пространства и найти координаты вектора b в этом базисе.
31.
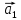(2; 1; 3), 
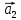(3; -1; 1), 
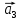(1; -1; -2), 
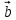(7; 0; 7).Проверим являются ли векторы
базисом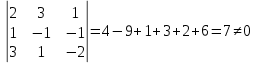
, то векторы образуют базис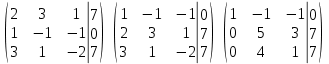
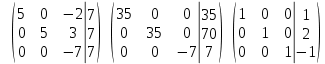
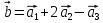
В задачах 41—50 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы
41.
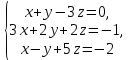
найдем ее решение матричным методом
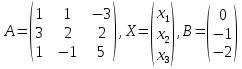
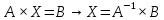
Найдем обратную матрицу
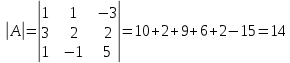
Найдем алгебраические дополнения
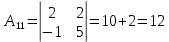
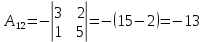
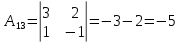
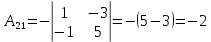
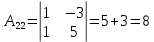
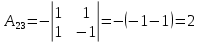
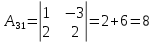
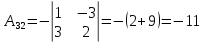
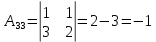
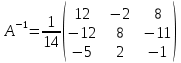
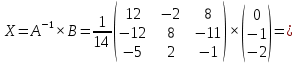
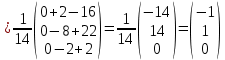
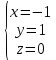
В задачах 51—70 найти указанные пределы (не пользуясь правилом
Лопиталя).
51. а)
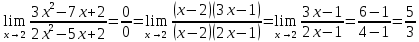
б)
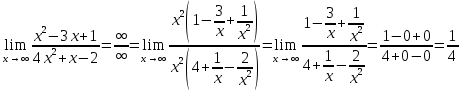
в)
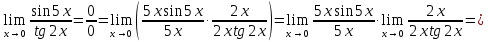
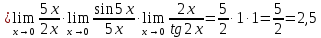
г)
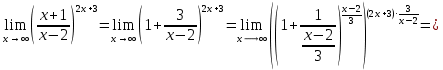
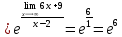
В задачах 71—90 найти производные функций.
71. а)
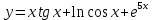
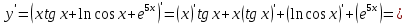
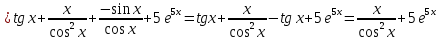
б)
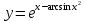
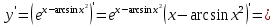
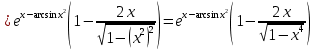
в)
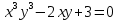
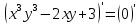
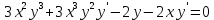
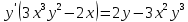
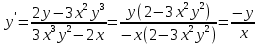
В задачах 91—110 исследовать данные функции методами дифференциального исчисления и построить их графики. Исследование функции рекомендуется проводить по следующей схеме: 1) найти область определения функции; 2) исследовать функцию на непрерывность; 3) определить, является ли данная функция четной, нечетной; 4) найти интервалы монотонности функции и точки ее экстремума; 5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба; 6) найти асимптоты графика функции.
91.
-
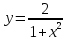
найти область определения функции
-
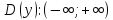
исследовать функцию на непрерывность
Из области определения видно, что функция не имеет точек разрыва, функция непрерывна.
-
определить, является ли данная функция четной, нечетной
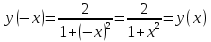
Функция четная, а значит симметричная относительно оси Оу.
-
найти интервалы монотонности функции и точки ее экстремума
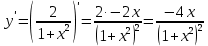
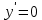при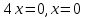 
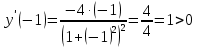
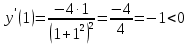
Функция возрастает на интервале
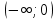и убывает на интеравале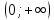 
Экстремум функции в точке с координатой Экстремум функции в точке с координатой
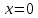, тогда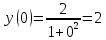 
-
найти интервалы выпуклости и вогнутости графика функции и точки перегиба
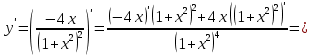
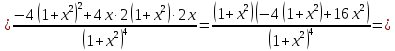
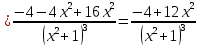
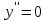при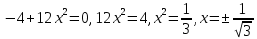 
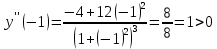
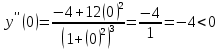
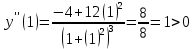
Функция вогнута на интервале
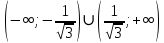и выпукла на интервале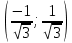 
Точки перегиба
-
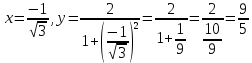
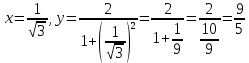
найти асимптоты графика функции.
Вертикальных асимптот нет, так как функция непрерывна на области определения
Найдем наклонную в виде:
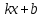
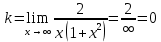
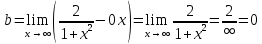
Горизонтальная асимптота
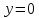
Построим график функции
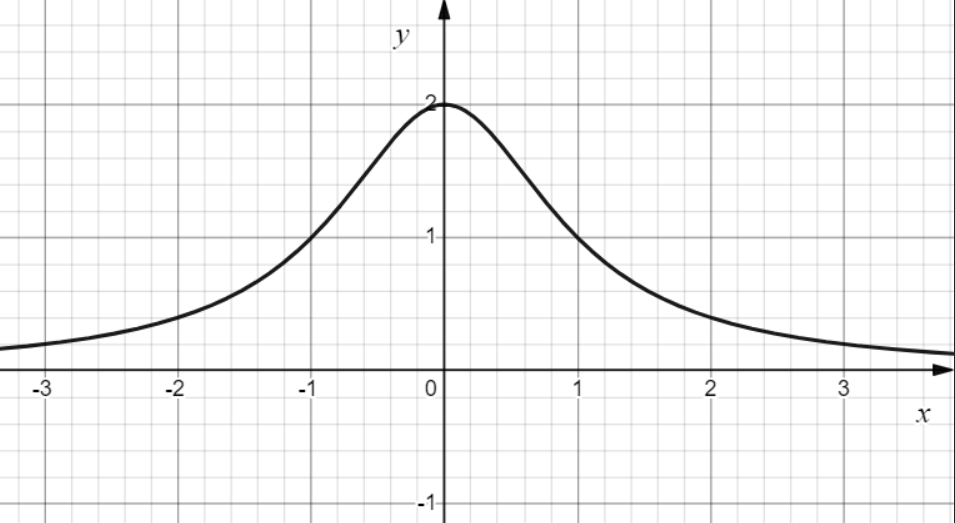
В задачах 131—150 найти указанные неопределенные интегралы и
результаты интегрирования проверить дифференцированием.
131. а)
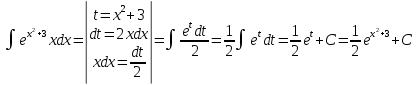
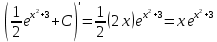
б)
 |  |
 |  |
 | |
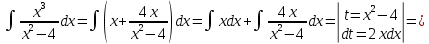
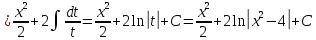
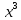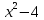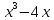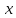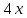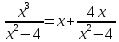
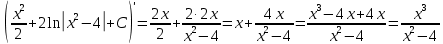
в)
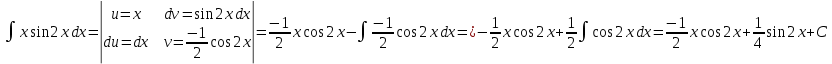
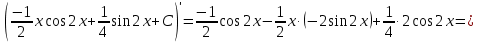
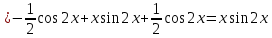
В задачах 151—160 вычислить площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
151.
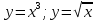
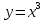– кубическая функция
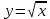– ветка параболаПостроим линии в одной плоскости
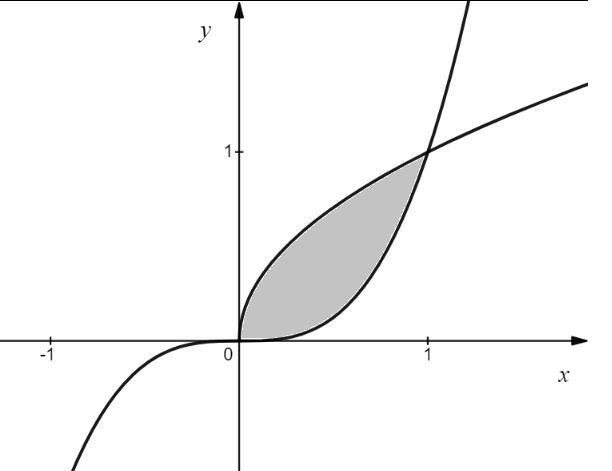
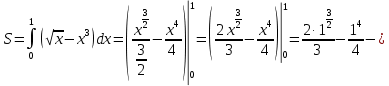
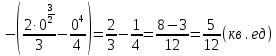
В задачах 161—165 вычислять объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной указанными линиями. Сделать чертеж.
161.
