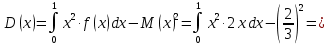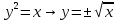
Обьем тела вращения вокруг оси Оx







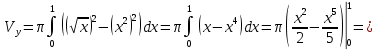
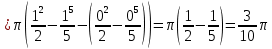
В задачах 171—190 найти общее решение дифференциальных уравнений первого порядка.

171.













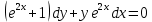
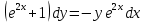
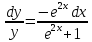
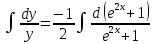
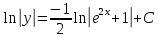
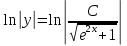
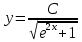
В задачах 191—200 найти частное решение дифференциального уравнения второго порядка, удовлетворяющее указанным начальным условиям.

191.

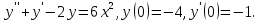
Найдем решение в виде

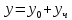
Найдем решение однородного уравнения











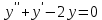
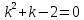
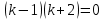
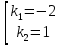
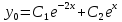
Найдем частное решение в виде

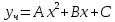
Найдем производные и подставим в начальное уравнение

---

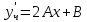
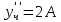
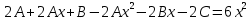
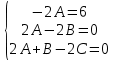
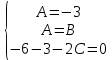
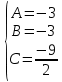
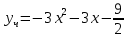
Общее решение



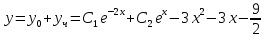
Найдем решение для указанных начальных условий















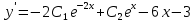
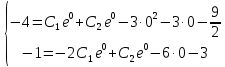
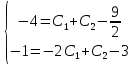
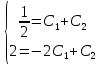
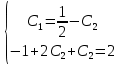
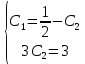
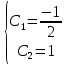
Решение дифференциального уравнения для начальных условий



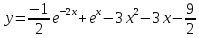
В задачах 201—220 дан степенной ряд. Найти интервал сходимости ряда

и исследовать его сходимость на концах интервала.

201.

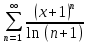
Степенной ряд в общем виде записывается следующим образом: ∑a_nxⁿ

где a_n – формула числовых коэффициентов. Для данного ряда:



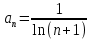
Областью сходимости степенного ряда является интервал (–R;R), где:



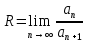
R – радиус сходимости. Вычислим его:







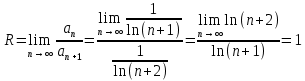
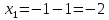
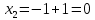
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-2;0)

Теперь проверим сходимость ряда на концах этого интервала.

Пусть x = -2

Получаем ряд:



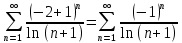
Исследуем сходимость ряда при помощи признаков сходимости.



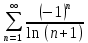
Рассмотрим первые три члена ряда:



Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.

---

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

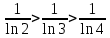
По второму признаку Лейбница предел ряда должен стремится к 0.



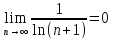
Второе условие Лейбница выполняется.

Таким образом, рассматриваемый ряд сходится.

Чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов.

Исходный ряд сравним с рядом:

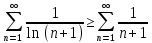– данный ряд расходится то и исследуемый ряд сходится условно.

Ряд сходится, значит, x = -2 – точка сходимости.

При x = 0

получаем ряд:



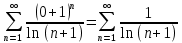
Исходный ряд сравним с рядом:

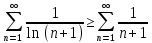– данный ряд расходится

Данный ряд исследовали выше, и он расходится, то x = 0 – точка расходимости.

Таким образом, данный степенной ряд является сходящимся при: x∈

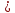
241. В читальном зале имеется 6 учебников по теории вероятностей, из которых три в мягком переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника окажутся в мягком переплете.

A – первый учебник имеет переплет

В – второй учебник имеет переплет

Вероятность того, что первый учебник в мягком переплете

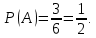
Вероятность того, что второй учебник имеет мягкий переплет, при условии, что первый учебник был в переплете:

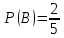
Искомая вероятность того, что оба учебника имеют переплет, по теореме умножения вероятностей событий равна



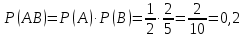
В задачах 271—280 задан закон распределения дискретной случайной величины Х (в первой строке указаны возможные значения величины X, во второй строке даны вероятноcти р этих значений). Найти:

---

1) математическое ожидание МХ; 2) дисперсию DX; 3) среднее квадратическое отклонение σ.

271.

X	8	4	6	5
p	0,1	0,3	0,2	0,4

1) Математическое ожидание находим по формуле MX = ∑x_ip_i.



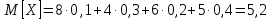
2) Дисперсию находим по формуле D = ∑x²_ip_i - M[x]².



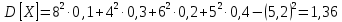
3) среднее квадратическое отклонение



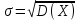
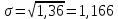
В задачах 281—290 случайная величина Х задана интегральной функцией распределения F(х). Найти: 1) дифференциальную функцию распределения f(х); 2) математическое ожидание МХ; 3) дисперсию DХ.

281.

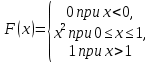
1) дифференциальную функцию распределения f(х);



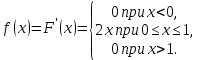
2) математическое ожидание МХ;



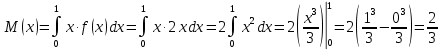
3) дисперсию DХ

---

Смотрите также файлы

• Билет номер 1.docx

• Теория менеджмента практическая .docx

• Вопросы правового регулирования.docx

• Исследование электронного и ионного фотоэлементов Ознакомиться с устройством и принципом действия фотоэлементов.docx

• Студент группы эс320(1).docx