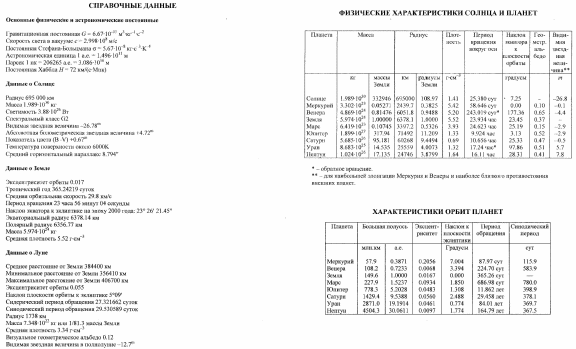
Критерии оценок: Максимальное количество баллов за задачу – 8

Задача решена полностью, получен правильный ответ, все объяснения корректны и достаточно подробны	8 баллов
Задача решена, однако объяснения не полны, либо не совсем верны	4 балла
Участник решил задачу, но с существенными ошибками, либо приведён ответ без каких-либо объяснений	2 балла
Задача не решена	0 баллов

Решения школьного этапа всероссийской олимпиады школьников по астрономии (2019)10 класс

1. 
   Расположите объекты в порядке увеличения их средней плотности: нейтронная звезда, Солнце, Бетельгейзе, белый карлик, Земля, кома кометы, Вселенная.
   

Решение: Вселенная, кома кометы, Бетельгейзе, Солнце, Земля, белый карлик, нейтронная звезда.

2. 
   На звездном небе 88 созвездий. Техника астрономических наблюдений постоянно улучшается, строятся новые и более мощные телескопы. Когда можно ожидать открытия новых созвездий? Поясните ответ.
   

Решение: Открытие новых созвездий ожидать не стоит. Так как в 1922 году в Риме, решением I Генеральной ассамблеи Международного астрономического союза был окончательно утверждён список из 88 созвездий, на которые было разбито звёздное небо. А в 1928 году были приняты чёткие и однозначные границы между этими созвездиями, проведённые строго по кругам небесной сферы прямых восхождений и дугам склонений в экваториальной системе небесных координат на эпоху 1875 г. В течение пяти лет в границы созвездий вносились уточнения. В 1935 году границы были окончательно утверждены, и астрономы договорились, что больше изменять их не будут.

3. 
   Определить время экспозиции t при фотографировании звёздного неба (см. рис.), если за этот промежуток времени звёзды описали дуги окружностей, соответствующие повороту небесной сферы на φ = 10°. Считать, что наблюдаются звёзды, находящиеся на высоте от 7° от горизонта (наблюдение осложнено оптическими явлениями в атмосфере).
   

---

Решение: Время, за которое произойдёт поворот небесной сферы, равно t = φ/ω, где ω – угловая скорость вращения.Земля (небесная сфера относительно наблюдателя) за T = 24 ч поворачивается на φ₀ = 360°, следовательно, угловая скорость вращения равна ω = φ₀/T.Получается, что время экспозиции равно t = φT/φ₀ = 10°∙24 ч/360° = 40 мин.

4. 
   Определить, на какое расстояниеS распространились радиоволны, излученные во время самых первых радиопередач человечества (примерно t = 125 лет назад). Ответ выразить в пк. Один парсек принять равным 1 пк = 3 ∙ 10¹⁶ м.
   

Решение: Расстояние, пройденное радиосигналом и выраженное в метрах, равноS = 3 ∙ 10⁸ м/с ∙ 125 лет = 3 ∙ 10⁸ м/с ∙ 125 ∙ 365 ∙ 24 ∙ 3600 с ≈ 1,18 ∙ 10¹⁸ м.Расстояние, выраженное в пк, равно S = 1,18 ∙ 10¹⁸ /3 ∙ 10¹⁶ пк ≈ 39 пк.

5. 
   Каждый год происходит хотя бы одно полное солнечное затмение с полосой полной фазы длиной 10 000 км и шириной 200 км (в среднем). Исходя из этого, оцените, как часто полное затмение происходит в определённом пункте Земли.
   

Решение: Площадь полосы полной фазы – 10 000 км × 200 км = 2 · 106 кв. км. Площадь земной поверхности 4 × 3,14 × (6400 км)2 ≈ 514 · 106 кв. км. Разделив второе на первое, получим 257. Если считать, что затмения во всех точках Земли равновероятны, то через конкретный пункт полоса полной фазы проходит в среднем один раз за 257 лет. С учётом оценочного характера задачи корректный ответ – раз в 200–300 лет.

6. 
   Для поддержания регулярной связи друг с другом и с Землей вокруг экватора Луны было решено построить цепочку из 60 высотных пунктов радиосвязи. При этом было необходимо, чтобы из каждого пункта были видны два соседних. Определите минимальную высоту пунктов связи. Радиус Луны равен 1738 км.
   

Решение: На рисунке показана предельная ситуация, при которой все пункты располагаются вдоль экватора Луны равномерно, и с одного пункта будут видны два соседних пункта прямо на лунном горизонте.Угол β с вершиной в центре Луны между направлениями на два соседние пункта равен 6, так как число пунктов равно 60 и они покрывают всю окружность экватора. Минимальная высота пунктов связи над поверхностью Луны составляет

---

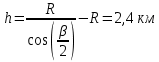.Здесь R ⸻ радиус Луны (1738 км).Критерии оценок: Максимальное количество баллов за задачу – 8

Задача решена полностью, получен правильный ответ, Все объяснения корректны и достаточно подробны	8 баллов
Задача решена, однако объяснения не полны, либо не совсем верны	4 балла
Участник решил задачу, но с существенными ошибками, либо приведён ответ без каких-либо объяснений	2 балла
Задача не решена	0 баллов

Решения школьного этапа всероссийской олимпиады школьников по астрономии (2019)11 класс

1. 
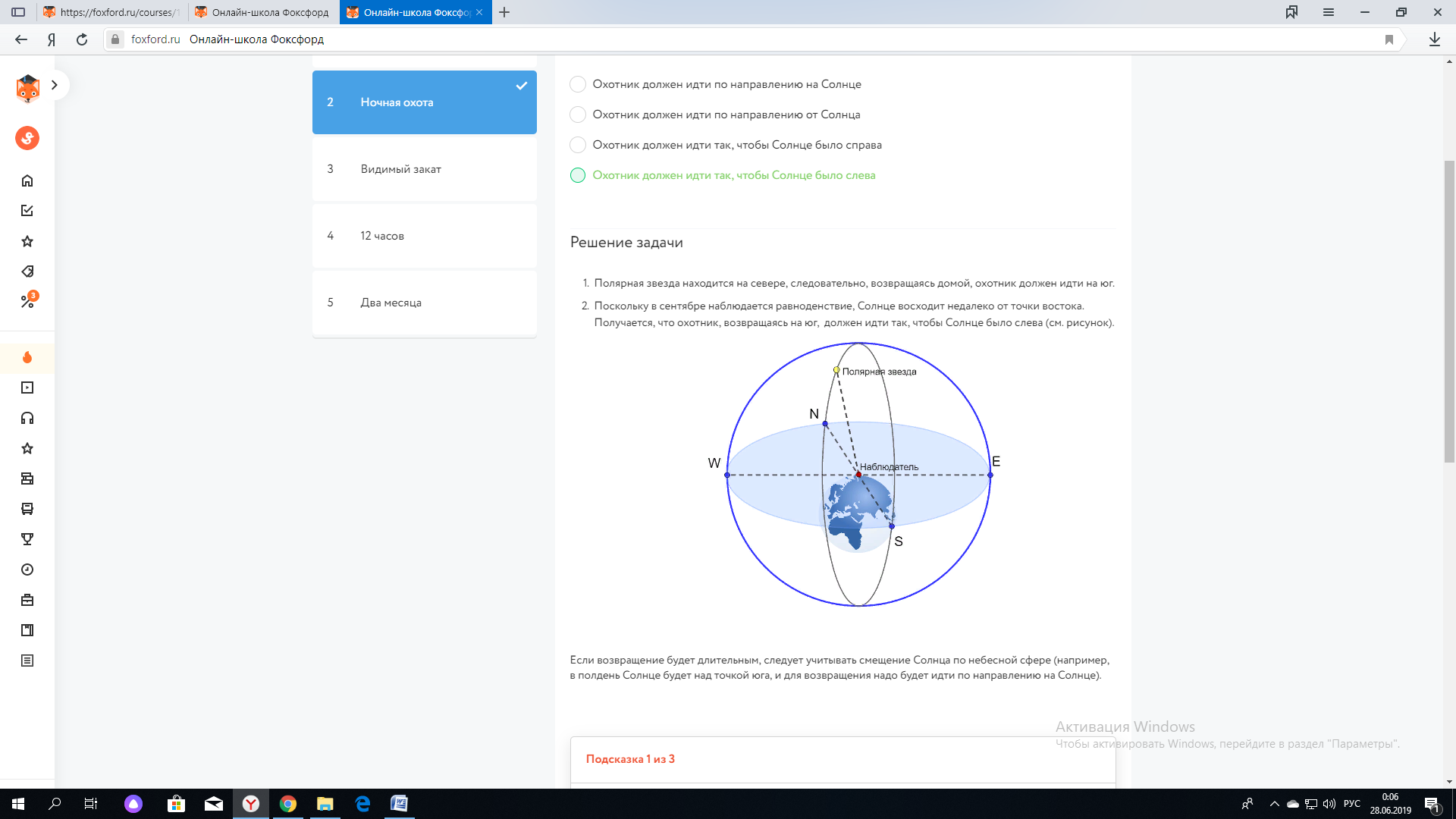   В сентябре охотник ночью идёт в лес по направлению на Полярную звезду. Сразу после восхода Солнца он возвращается обратно. Как должен охотник ориентироваться по Солнцу? Действие происходит в средних широтах северного полушария. Обратный путь занимает не более часа.
   

Решение: Полярная звезда находится на севере, следовательно, возвращаясь домой, охотник должен идти на юг. Поскольку в сентябре наблюдается равноденствие, Солнце восходит недалеко от точки востока. Получается, что охотник, возвращаясь на юг, должен идти так, чтобы Солнце было слева (см. рис.). Если возвращение будет длительным, следует учитывать смещение Солнца по небесной сфере (например, в полдень Солнце будет над точкой юга, и для возвращения надо будет идти по направлению на Солнце).

2. 
   Используя карту, определите экваториальные координаты звезды Спика (α Девы).
   

Решение: По рисунку видно, что прямое восхождение звезды Спика равноα ≈ 13 ч 25 мин, а склонение этой звезды равно δ ≈ −11^°10′.

3. 
   Ускорение свободного падения на Марсе и на Меркурии примерно одинаковое – 3,7 м/с². Однако Меркурий в 1,4 раза меньше Марса по диаметру. Сравните плотности планет.
   

---

Справочные данные: Объём шара V = 4πR³/3, где R – его радиус.Решение: Ускорение свободного падения на поверхности планеты зависит от её массы и радиуса g = GM/R². Т.к. ускорения одинаковы, M₁/R₁² = M₂/R₂². (1 – Марс, 2 – Меркурий; d₁/d₂ = 2).Массу планеты можно выразить через радиус и среднюю плотность: M = 4πR³ρ/3.После подстановки массы в предыдущее равенство получаем ρ₁R₁ = ρ₂R₂.Следовательно, плотность Меркурия больше плотности Марса в 1,4 раза.

4. 
   Двигаясь невысоко над поверхностью Земли (от 200 до 1000 км), искусственный спутник испытывает заметное сопротивление атмосферы. Как при этом изменяется его скорость: увеличивается или уменьшается?
   

Решение:Казалось бы, под действием сопротивления воздуха скорость аппарата должна уменьшаться, как это происходит, например, с любым автомобилем, который катится по инерции. Но у спутника, в отличие от автомобиля, нет твердой опоры. Теряя энергию за счет сопротивления воздуха, он не может сохранить высоту полёта и начинает приближаться к Земле. При этом за счет её притяжения он разгоняется и увеличивает свою скорость.

5. 
   Пульсар PSR J1748−2446ad вращается вокруг своей оси с периодом T = 1,4 мс (это пример наиболее быстрого вращения среди известных звёзд). Оцените минимальную допустимую среднюю плотность указанного пульсара, при которой силы гравитации ещё удержат звезду от разлёта.
   

Справочные данные: Гравитационная постоянная G = 6,7·10⁻¹¹ м ³/(кг·с²), объём шара V = 4πR³/3, где R – его радиус.Решение: Для удержания вещества от разлёта ускорение свободного падения на поверхности пульсара g = GM/R² (совместно с нормальной реакцией ниже лежащих слоёв звезды) должно обеспечивать необходимое максимальное центростремительное ускорение: a = V²/R = (2πR/T)²/R = 4π²R/T² точек на экваторе,где V = 2πR/T — экваториальная скорость, R — радиус пульсара.Выражаем массу M в виде 4πR³ρ/3 (т.е. через плотность вещества ρ и его объём), что даёт эквивалентное выражение для ускорения свободного падения g = 4πGρR/3.Тогда указанное выше условие (g ≥ a) запишется в виде 4πGρR/3 ≥ 4π²R/T², откуда искомое ограничение снизу на плотность веществаρ = 3π /GT² = 3 × 3,14 / [6,7 · 10⁻¹¹ м³/(кг · с²) × (1,4 · 10⁻³ с)²] = 7,2 · 10¹⁶ кг/м³.

6. 
   Сколько всего дней будет в XXI веке?
   

---

Решение: Первый день XXI века – 1 января 2001 года, последний – 31 декабря 2100 года.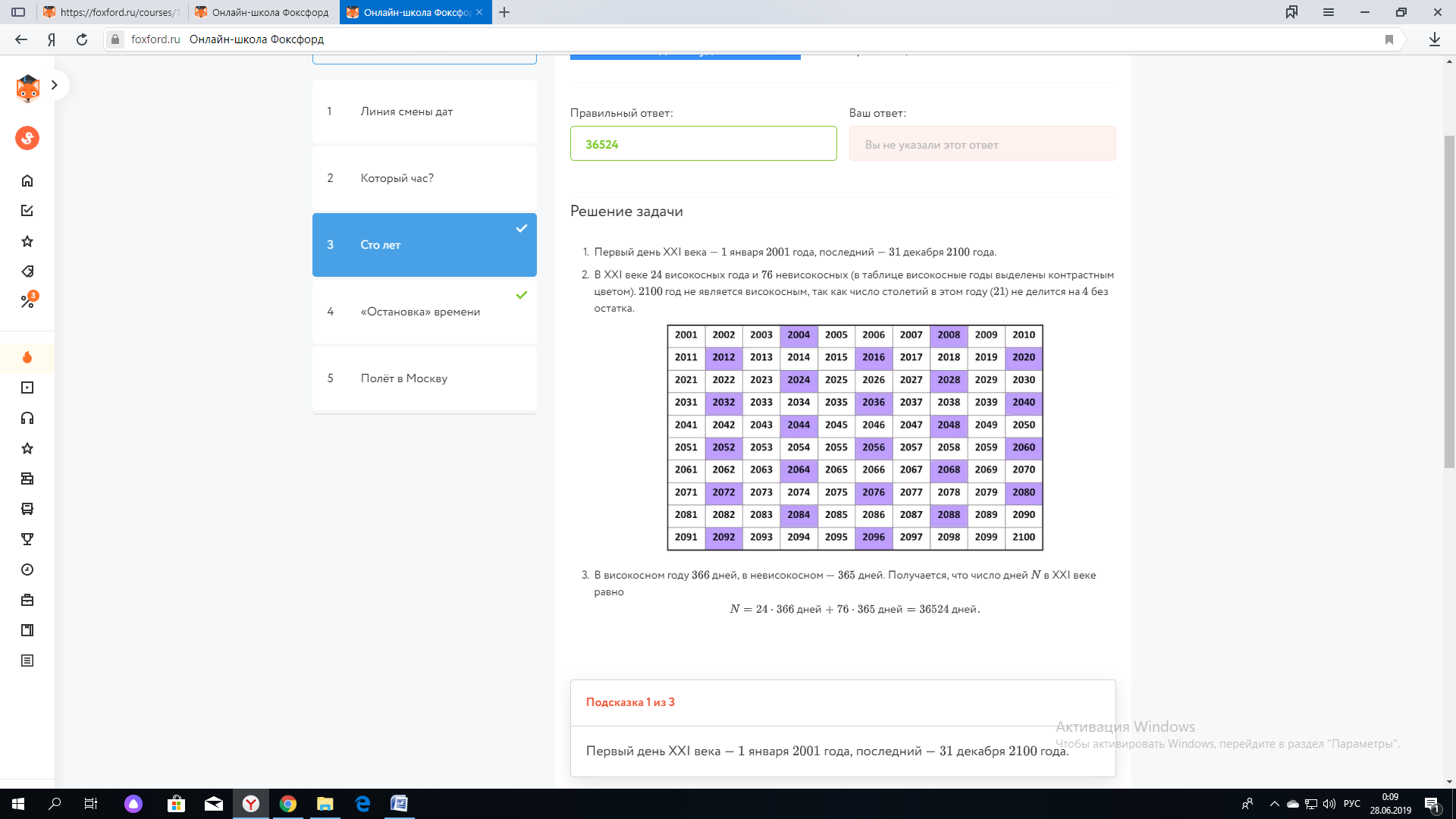В XXI веке 24 високосных года и 76 невисокосных (в таблице високосные годы выделены контрастным цветом). 2100 год не является високосным, так как число столетий в этом году (21) не делится на 4 без остатка.В високосном году 366 дней, в невисокосном – 365 дней.Тогда число дней в XXI веке равно 24 ∙ 366 + 76 ∙ 365 = 36524 дней.Критерии оценок: Максимальное количество баллов за задачу – 8

Задача решена полностью, получен правильный ответ, Все объяснения корректны и достаточно подробны	8 баллов
Задача решена, однако объяснения не полны, либо не совсем верны	4 балла
Участник решил задачу, но с существенными ошибками, либо приведён ответ без каких-либо объяснений	2 балла
Задача не решена	0 баллов

Участнику

---

Смотрите также файлы

• Дополнительное образование детей история и современность (пдо, 2 часть).docx

• Методические рекомендации по огп Приказ мчс россии 472 от 26. 10. 2017 Об утверждении Порядка подготовки личного состава пожарной охраны.docx

• Тем Транспортный комплекс Российской Федерации Задание 1.docx

• Исламова А. Г.docx

• Фгбоу во юурггпу профессиональнопедагогический институт.docx