Микрогетерогенные системы (взвеси, порошки, эмульсии, пены). Размер частиц 1^.10^–4–1^.10^–7 м. Эти системы термодинамически неустойчивы: довольно быстро разрушаются вследствие оседания частиц. Частицы не способны к диф-фузии, не проходят даже через бумажные фильтры, видны в оптический микро-скоп. Растворы мутны вследствие поглощения света, отражения и преломления его частицами. Примеры: взвеси глины, ила, песка в воде, облака пыли, порошки и др.

Классификация по агрегатному состоянию дисперсной фазы и дисперсионной среды (по В.Оствальду)

Учитывая, что вещество может находиться в трех агрегатных состояниях, возможны 8 комбинаций дисперсионной среды и ДФ:

ДС	ДФ	Условное обозначение системы	Тип системы	Примеры
Газ	Газ Жидкость Твердое тело	Г–Г Г–Ж Г–Т	Аэрозоли	Нет (гомогенные системы). Туман, облака, аэрозоли жидких лекарств. Дым, пыль, порошки, аэрозоли твердых лекарств.
Жидкость	Газ Жидкость Твердое тело	Ж–Г Ж–Ж Ж–Т	Лиозоли	Пены, крем, газированная вода Эмульсии, нефть, молоко, сливки. Суспензии, зубные пасты, тушь, глины.
Твердое тело	Газ Жидкость Твердое тело	Т–Г Т–Ж Т–Т	Солидозоли	Твердые пены (пемза, хлеб, резина, лава, пенобетон, пенопласт) Жемчуг, некоторые минеральные гели, опал, желе, желатин, агар-агар Сплавы, стекла, минералы (рубин)

Для отличия коллоидных растворов от других дисперсных систем, их называют золями (от лат. solutio раствор). Поэтому системы, в которых дисперсионной средой является газ называют аэрозолями, в случае жидкости – лиозолями, в случае твердой дисперсионной среды – солидозолями. В зависимости от природы жидкой дисперсионной среды лиозоли делят на гидрозоли, алказоли, бензозоли, этерозоли (органозоли).
Классификация по взаимодействию дисперсионной среды и дисперсной фазы (по Г.Фрейндлиху)

---

Такая классификация пригодна только для систем с жидкой дисперсионной средой.

Если поверхность частиц и молекула растворителя имеют одинаковую по-лярность (т.е. сродство), то они будут взаимодействовать друг с другом. Поэто-му вокруг коллоидных частиц образуются толстые многослойные сольватные оболочки. Фрейндлих таких систем назвал лиофильными (от гр. lyo жидкость + phileo люблю). Примерами таких систем являются растворы белка, крахмала, агар-агара, гуммиарабика, высококонцентрированные эмульсии, эмульсолы. В случае, когда частицы и молекулы растворителя разнополярны, то между коллоидными частицами и дисперсионной средой отсутствует взаимодействие, значит отсутствуют и сольватные оболочки, либо образуются тонкие сольватные оболочки. Такие системы были названы лиофобными коллоидными растворами (от гр.lyo жидкость + phobos боязнь). В случае, когда дисперсионной средой является вода, эти системы называются соответственно, гидрофильными и гидрофобными.

К лиофобным системам относятся типичные коллоидные системы, образо-ванные трудно растворимыми в дисперсионной среде веществами (слабые осно-вания, некоторые соли, металлы, аэрозоли, пены).

Лиофильные системы не обладают всеми типичными коллигативными свойствами, они растворяются самопроизвольно, термодинамически устойчивы, образуют гомогенные растворы. Поэтому лиофильных систем в настоящее время выделяют как особые группы дисперсных систем – растворы высокомо-лекулярных веществ (белков, полисахаридов, нуклеиновых кислот) и мицелярные растворы ПАВ.

Классификация по взаимодействию между частицами дисперсной фазы

(по подвижности дисперсной фазы)

Р.Зигмонди дисперсные системы разделил на свободнодисперные и связнодисперсные. В свободнодисперсных системах (золях, эмульсиях) частицы не связаны друг с другом, свободно перемещаются в дисперсионной среде под действием броуновского движения или силы тяжести. Лиозоли обладают текучестью.

В связнодисперсных системах частицы взаимодействуют друг с другом, под действием физических сил образуют пространственные сетки, структуры, поэтому не могут перемещаться. Такая система не может течь. Их называют гелями и студнями. К ним относятся пасты, концентрированные эмульсии, суспензии, пены, порошки, кремы.

---

Лекция 2

МОЛЕКУЛЯРНО-КИНЕТИЧЕСКИЕ и ОПТИЧЕСКИЕ СВОЙСТВА КОЛЛОИДНЫХ СИСТЕМ

Молекулярно-кинетические свойства коллоидных систем, как и истинных растворов обнаруживаются в таких явлениях, как броуновское движение, диф-фузия, осмотическое давление и они связаны движением дисперсных частиц. Поскольку коллоидные частицы участвуют в тепловом движении и подчиняются молекулярно-кинетическим законам обычных растворов, экспериментально можно определить размер, массу и концентрацию частиц дисперсной фазы.

---

Диффузия. Диффузия – это самопроизвольный необратимый процесс вырав-нивания концентрации частиц по всему объёму раствора или газа под влиянием теплового движения. Процесс диффузии идёт самопроизвольно, поскольку он сопровождается увеличением энтропии системы, так как по второму закону тер-модинамики, равномерное распределение вещества в системе отвечает наиболее вероятному её состоянию. Для описания диффузии в коллоидных системах более справедливо применение I закона Фика:

,

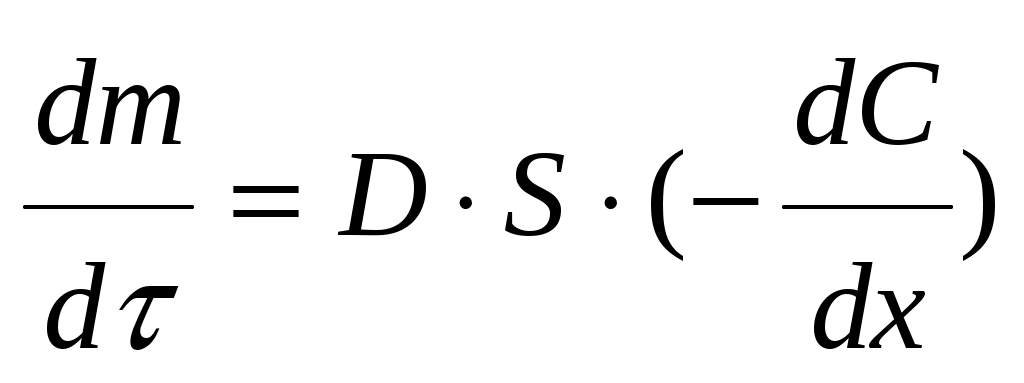где 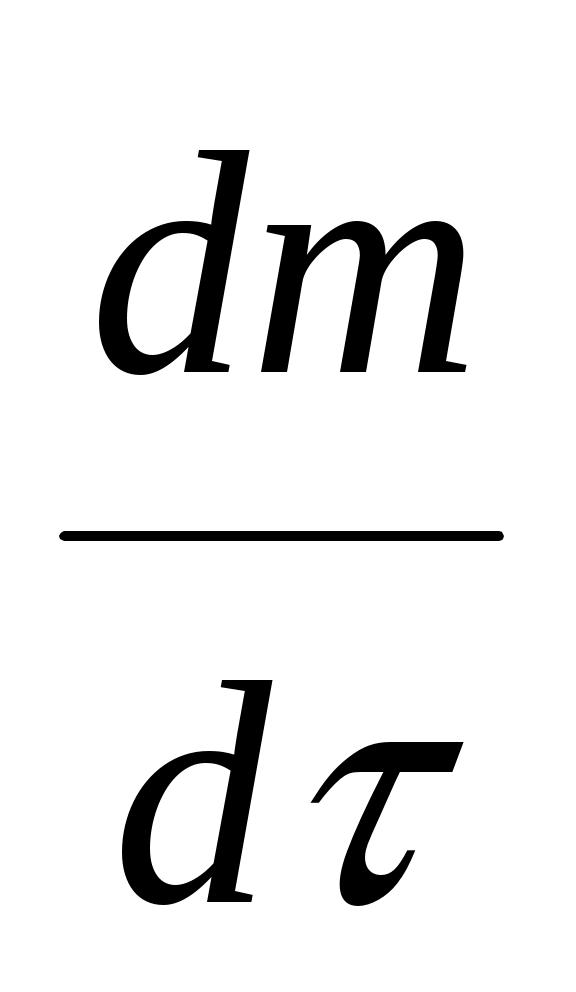- масса вещества, диффундированного за единицу времени; 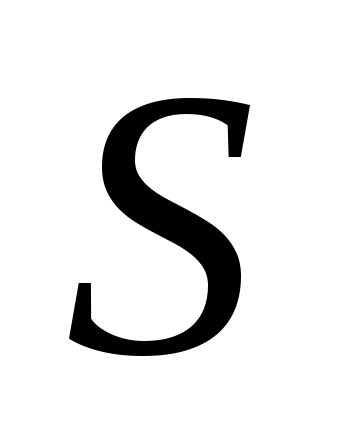- пло-щадь диффузии, 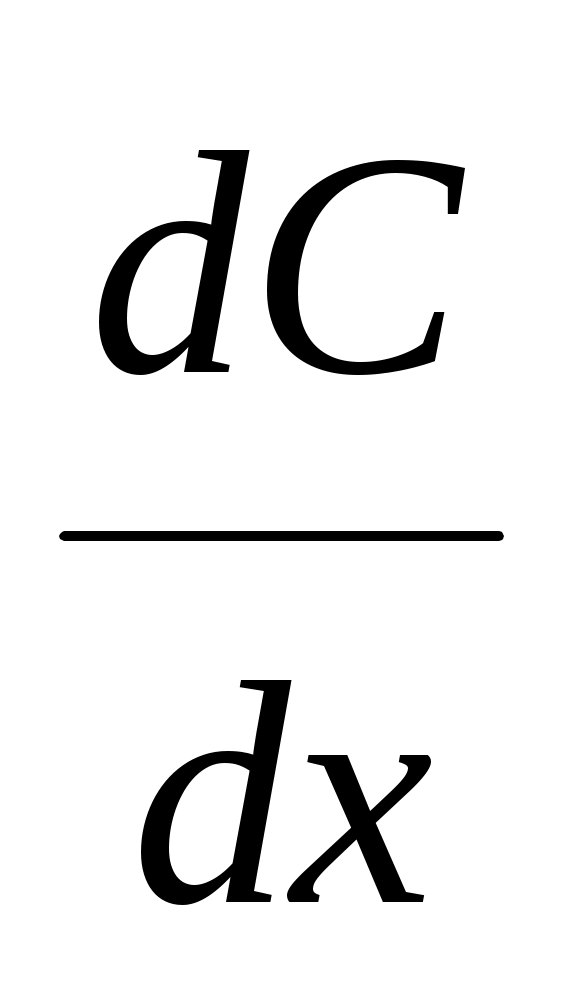- градиент концентрации (знак «-» означает, что диффузия идёт в сторону уменьшения концентрации); 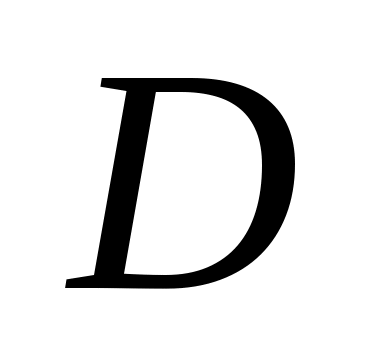– коэффициент диффузии; это масса вещества, продиффундированного за единицу времени через единицу площади при градиенте концентрации, равном единице 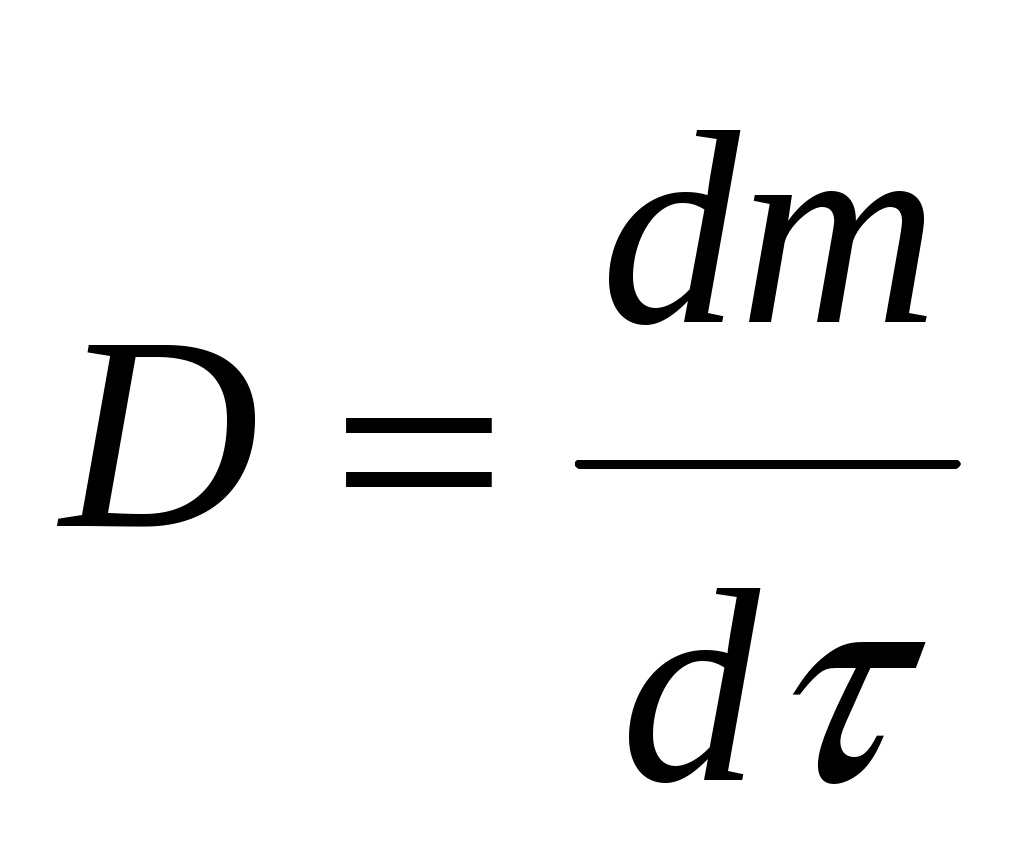, т.е. масса вещества диффундирущего за единицу времени через поперечное сечение в 1 м² при 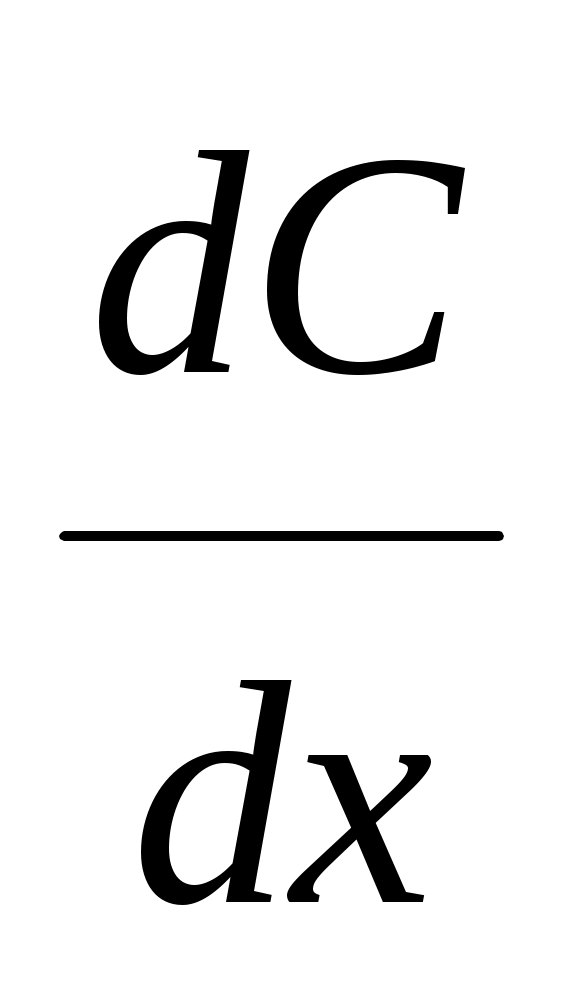= 1 (физический смысл коэффициента диффузии).

Эйнштейн показал, что коэффициент диффузии связан с размерами частиц, вязкости дисперсионной среды, температуры: 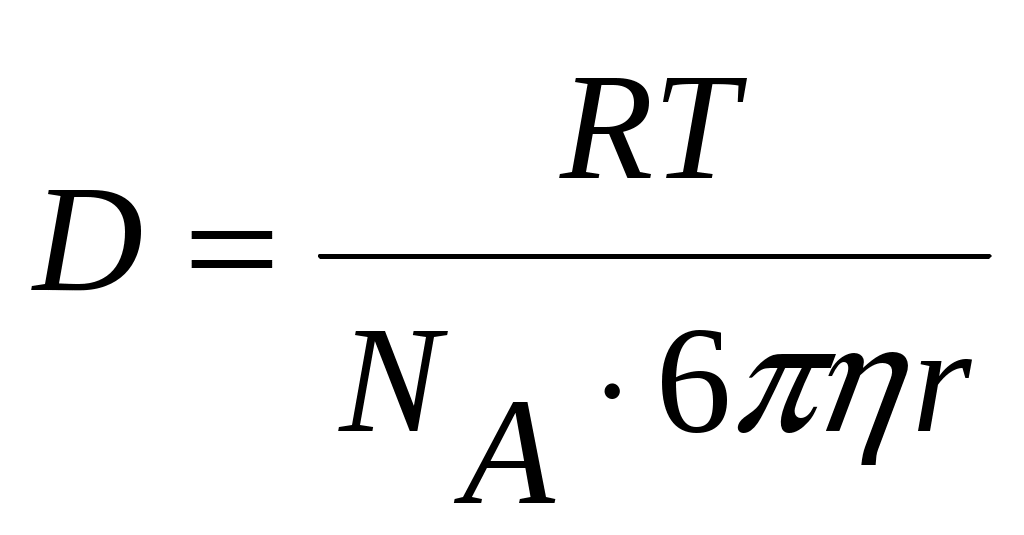, м²/с. Как видно из формулы, чем меньше размер частиц, тем больше коэффициент диффузии. Для коллоидных систем D

10^-13 м²/с.

Так как в коллоидных системах размер частиц дисперсной фазы значительно больше размера молекул или ионов, скорость диффузии в коллоидных системах в целом небольшая, т.е. меньше скорости диффузии в истинных растворах.

Используя уравнение Эйнштейна можно определить размер частиц золей и молекулярную массу полимера. Для этого требуется экспериментально опреде-лить D. С этой целью, сначала оптическими методами, измеряя показатель пре-ломления или оптическую плотность раствора, измеряют скорость изменения концентрации в слое, а затем рассчитывают значение D.

В тех случаях, когда затруднено определение D через концентрацию, D и r частиц рассчитывают через смещение частиц.

После определения размера частиц можно рассчитать мицеллярную массу частиц или молекулярную массу полимера (что и было сделано впервые для белков). Для этого пользуются уравнением Перрена:

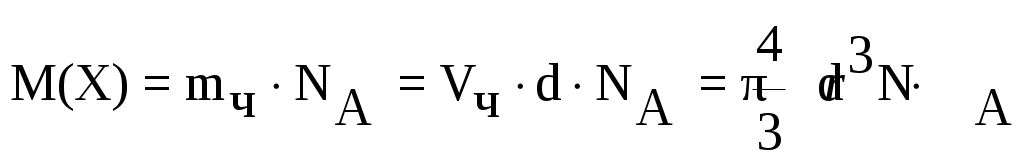,(а.е.м)

где 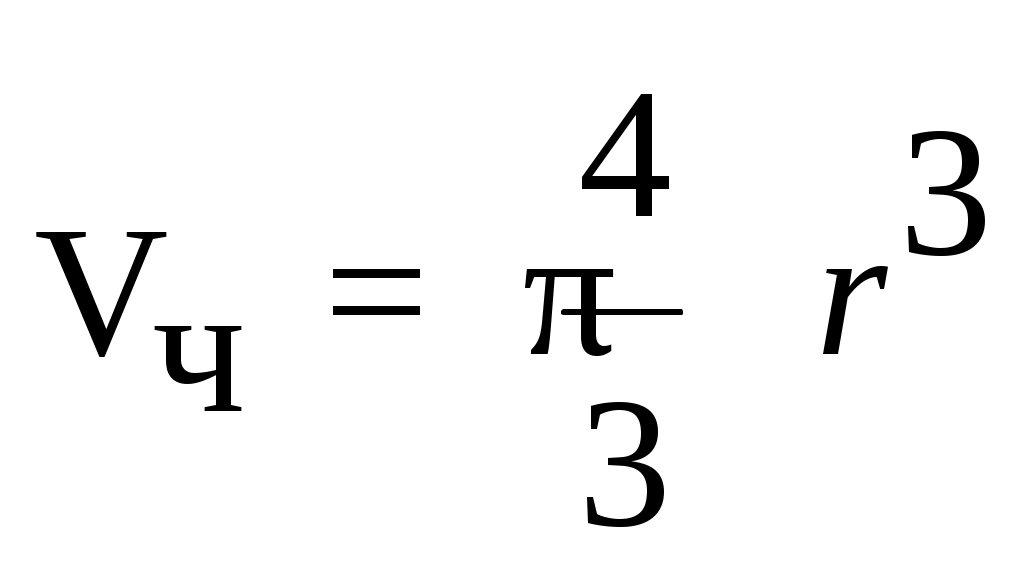– объем одной частицы; d – плотность вещества.

Броуновское движение

Историческая справка: Броуновское движение наблюдал Р.Браун под микроско-пом водной суспензии цветочной пыльцы в 1828 г. Оно количественно было исследовано в 1906 году французским ученым Ж.Перреном. На основе опытов он вычислил число Авогадро, за что получил Нобелевскую премию.

Броуновское движение проявляется в хаотическом и непрерывном движении частиц ДФ под действием ударов молекул дисперсионной среды, находящихся в состоянии интенсивного молекулярно-теплового движения. В зависимости от размера частиц их движение может иметь различные формы. Частицы коллоид-ных размеров под действием ударов молекул ДС с разных сторон, могут переме-щаться поступательно в разных направлениях. Траектория движения таких час-тиц представляет собой ломаную линию неопределенной конфигурации (рис.1).

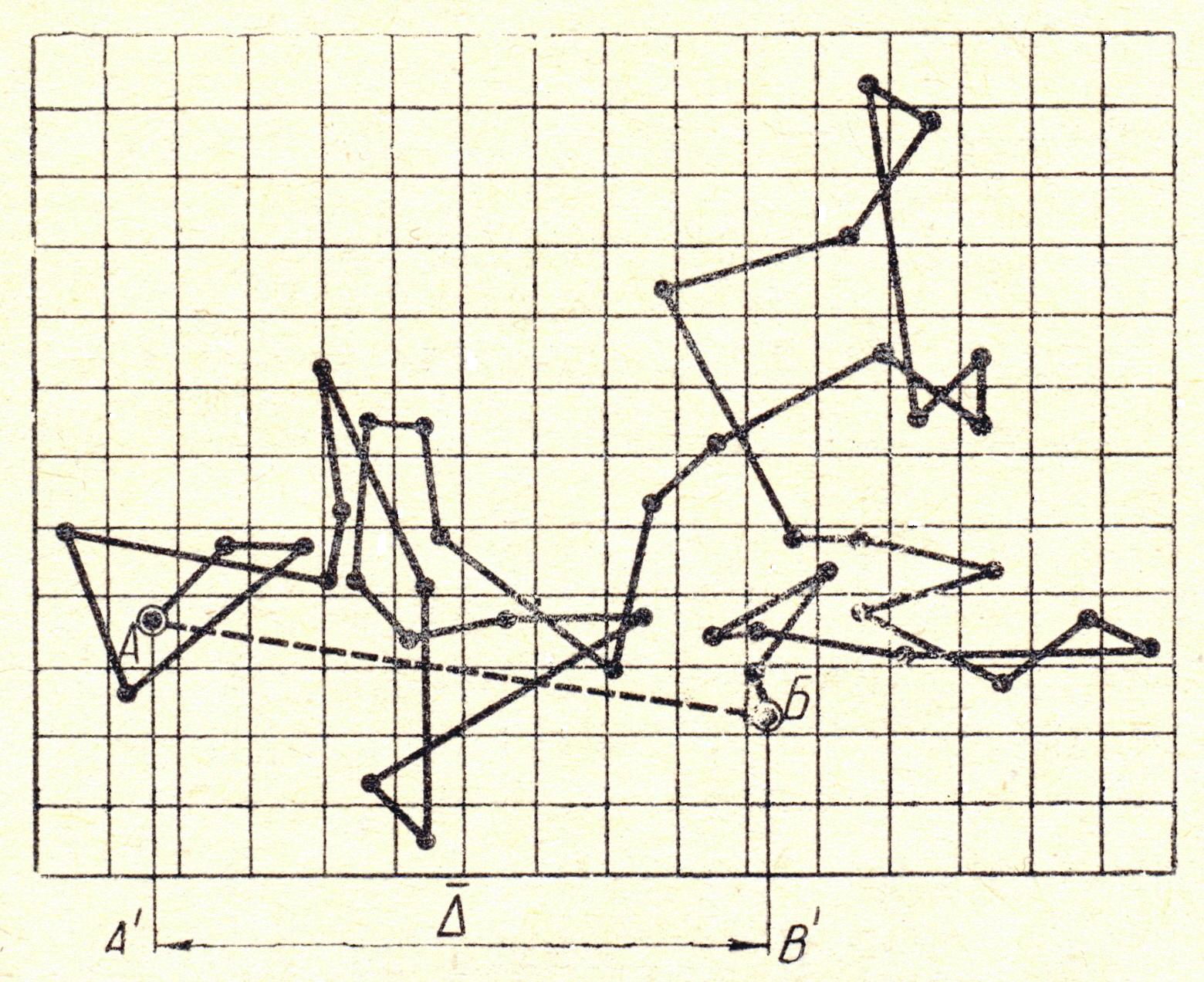Рис.1 Схема броуновского движения одной частицы

Количественной мерой (интен-сивности броуновского движе-ния) принимают величину сред-него смешения (сдвига) частицы за определенный промежуток времени. Смещением частицы называют расстояние между проекциями начальной и конечной точек траектории на ось смещений. А.Эйнштейн и М.Смолуховский показали, что смещение части-цы не зависит от природы кол-лоидной системы, а определя-ется лишь размером частицы (r) и растет со временем (t).

---

На него оказывают влияние температура (t) и вязкость среды (h):

,

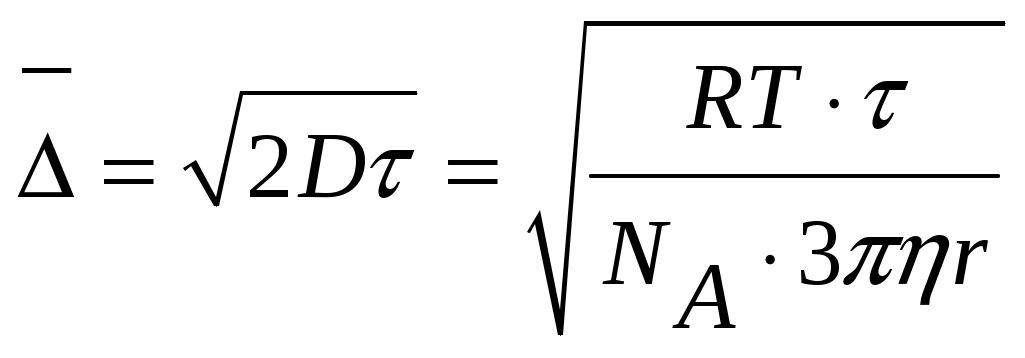где R – универсальная газовая постоянная, N_A – число Авогадро,

– коэффициент диффузии.

Как видно из уравнения, смещение частицы обратно пропорционально радиусу частицы. Это означает, что чем крупнее частица, тем меньше величина её смеще-ния. С увеличением размера частицы броуновское движение ослабевает и при каких-то размерах прекращается. Для частиц размером более 50 нм броуновское движение вообще не характерно. Броуновское движение наблюдают под микро-скопом или кинематографической микросъёмкой и используя уравнение рассчи-тывают размер коллоидных частиц.

Осмотическое давление коллоидных растворов. Осмос – сампроизвольный односторонний переход молекул дисперсионной среды через полупроницаемую мембрану из раствора с меньшей концентрацией в раствор с большей концентра-цией, т.е. односторонняя диффузия через полупроницаемую мембрану. За счет диффузии молекул дисперсионной среды через мембрану наблюдается увеличе-ние объёма раствора с большей концентрацией. Работа системы против внешнего давления (изменение объема раствора) описывается осмотическим давлением. Равновесное осмотическое давление растворов неэлектролитов рассчитывают по уравнению Вант-Гоффа: . Осмотическое давление – это свойство, определяемое числом частиц в растворе. Поэтому в случае коллоидных систем определяют по уравнению: , где - численная (или частичная) концентрация. Численная концентрация представляет собой число частиц в 1 л дисперсной системы и её можно вычислить по соотношению . Тогда = , а .

Как видно из уравнения, осмотическое давление пропорционально числу час-тиц в единице объема системы и не зависит от природы и массы частиц. Коллоидные растворы разных веществ с одинаковой численной концентрацией молекул или частиц оказывают одинаковое осмотическое давление. Например, при 273К при

---

Смотрите также файлы

• Курсовая работа по дисциплине Документационное обеспечение деятельности предприятия.doc

• Российский биотехнологический университет Кафедра Управление бизнесом и сервисные технологии.docx

• Дипломная работа включает введение, основную часть, заключение, список использованных источников, приложения (при их наличии). Введение.docx

• Государственный строительный комитет ссср.doc

• Ответы Императивная, материальная, постоянная, общенациональная.doc