Файл: Контрольная работа 1. Вариант Элементы векторной алгебры аналитической геометрии и линейной алгебры.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа №1. Вариант 9.
Элементы векторной алгебры аналитической геометрии и линейной алгебры.
1.9 Найти объем параллелепипеда, построенного на векторах:
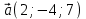 ,
, 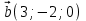
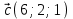 . Сделать чертеж.
. Сделать чертеж.Решение
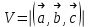
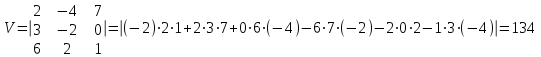 (ед3)
(ед3)
2.9. Даны уравнения двух медиан треугольника х-2у+1=0 и у-1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж.
Решение.
Пусть т.В имеет координаты (х1;у1), т.к. точка К по условию есть середина отрезка АВ, то ее координаты равны
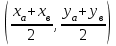 и удовлетворяют уравнению х-2у+1=0, то
и удовлетворяют уравнению х-2у+1=0, то 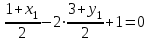 . Кроме того координаты точки В(х1;у1) удовлетворяют уравнению у-1=0, получаем систему линейных алгебраических уравнений
. Кроме того координаты точки В(х1;у1) удовлетворяют уравнению у-1=0, получаем систему линейных алгебраических уравнений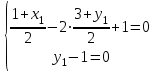
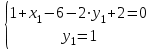
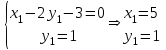 , т. В(5;1)
, т. В(5;1)Аналогично найдем координаты точки С(х2;у2). Пусть N – середина отрезка АС, тогда координаты точки находятся по формулам
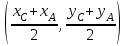 ,
, 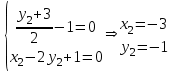 т. С(-3,-1).
т. С(-3,-1).Если даны две точки (х1,у1) и (х2,у2) , то уравнение линии, проходящей через эти точки вычисляется по формуле :
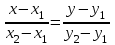
Уравнение АВ:
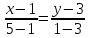 или
или 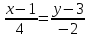 или х+2у-7=0 (АВ)
или х+2у-7=0 (АВ)Уравнение ВС:
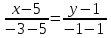
или
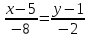 или х-4у-1=0 (ВС)
или х-4у-1=0 (ВС)Уравнение АС:
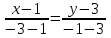 или
или 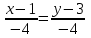 или х-у+2=0 (АС)
или х-у+2=0 (АС)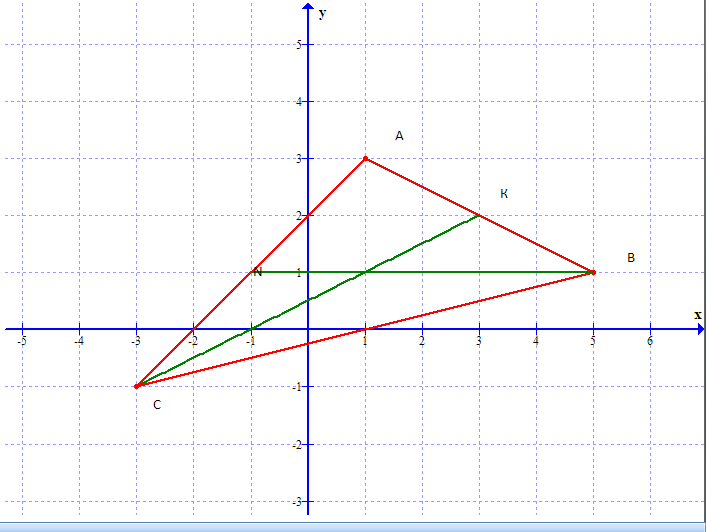
Ответ: х-у+2=0 (АС), х-4у-1=0 (ВС), х+2у-7=0 (АВ)
3.9. Решить систему линейных уравнений по правилу Крамера и методом Гаусса. Сделать проверку.
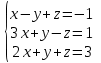
Решение.
1) Метод Крамера. Если
 ¹0, то систему можно решить по формулам Крамера:
¹0, то систему можно решить по формулам Крамера: х1 =
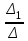 , х2 =
, х2 = 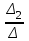 , ..., хn =
, ..., хn = 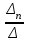 , – где D=
, – где D= , а Dk – определитель матрицы, полученной из матрицы А заменой k-го столбца столбцом свободных членов.
, а Dk – определитель матрицы, полученной из матрицы А заменой k-го столбца столбцом свободных членов.Для решения системы по правилу Крамера найдем следующие определители:
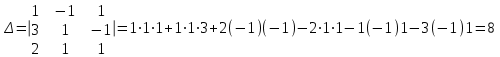
Так как данный определитель не равен нулю, то данная система имеет единственное решение, а значит система совместна.
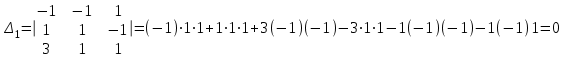
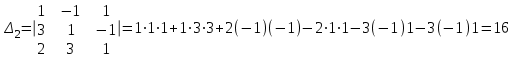
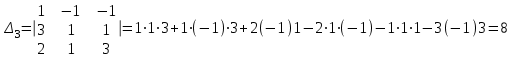
Тогда решение системы находим по формулам:
x1 =
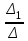 = 0; x2 =
= 0; x2 = 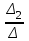 = 2; x3 =
= 2; x3 = 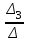 =1
=1 2) Для решения системы методом Гаусса рассмотрим расширенную матрицу системы и приведем ее к треугольному виду:
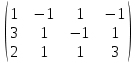 = [умножаем первую строчку на -3 и складываем со второй, умножаем первую на -2 и складываем с третьей] =
= [умножаем первую строчку на -3 и складываем со второй, умножаем первую на -2 и складываем с третьей] =
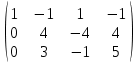 = умножаем вторую строку на
= умножаем вторую строку на 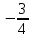 и складываем с третьей] =
и складываем с третьей] = 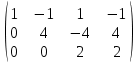
Получаем систему:
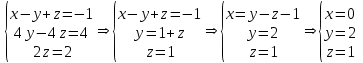
Получаем х=0, у=2, z=1.
Проверка: Подставим полученные значения переменных в исходную систему уравнений:

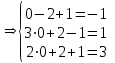 Получаем верные равенства
Получаем верные равенстваОтвет: х=0, у=2, z=1
Введение в математический анализ. Производная и ее приложения.
4.9. Найти пределы функций, не пользуясь правилом Лопиталя.
Решение:
а)
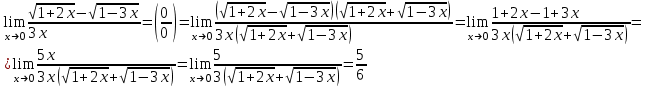
б)
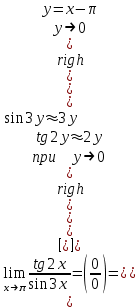
в)
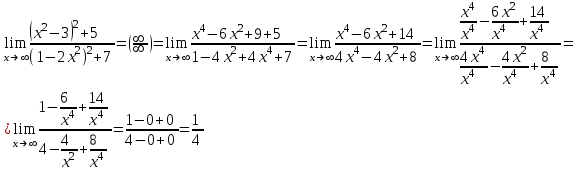
г) использовали второй замечательный предел
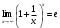
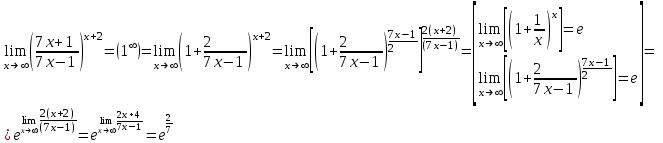
Ответ:
а)
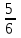
б)
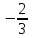
в)
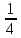
г)
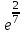
5.9. Задана функция y=f(x). Найти точки разрыва функции, если они существуют. Сделать схематический чертеж.
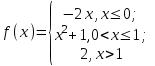
Решение.
Данная функция определена для всех значений х
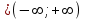 и на каждом из участков задания (-∞,0), (0,1), (1, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=0 и х=1.
и на каждом из участков задания (-∞,0), (0,1), (1, +∞) является элементарной и, следовательно, непрерывной. Непрерывность функции может нарушиться лишь в точках, где изменяется ее аналитическое значение, то есть в точках х=0 и х=1.
Исследуем эти точки на непрерывность, находя односторонние пределы:




0
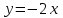
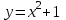
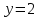

1
При х=0
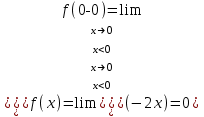
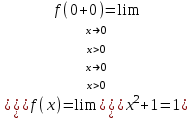
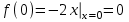

Так как в точке х=0 односторонние пределы – конечные числа, но не равны между собой, то х=0 – точка разрыва 1-го рода.
При х=1
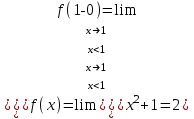
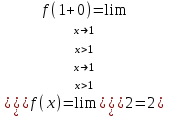
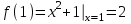
в точке х=1 f(1-0)=f(1+0)=f(1), значит х=1 точка непрерывности функции.
Построим схематический график.



у=х2+1
у=-2х
у=2
О
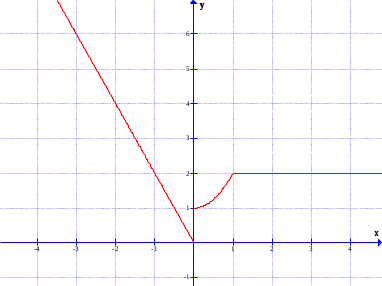 твет: х=0 – точка разрыва 1-го рода.
твет: х=0 – точка разрыва 1-го рода. 6.9. Методами дифференциального исчисления:
А) исследовать функцию
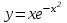 для
для 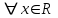 и по результатам исследования построить ее график;
и по результатам исследования построить ее график;Б) найти наименьшее и наибольшее значения заданной функции на отрезке [-2;2].
Решение.
-
Область определения функции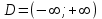 функция непрерывна
функция непрерывна -
Точки пересечения с осями координат:
Ох:
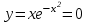 при
при 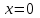 , получаем точку О(0;0)
, получаем точку О(0;0) Оу: х=0 y=0 т.(0; 0) – точка пересечения.
-
Функция является нечетной, т.к.
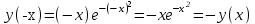
-
Экстремумы и монотонность. Вычисляем первую производную
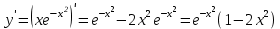
Находим критические точки
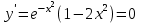 при х=
при х=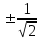
| х | (-∞; 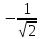 ) ) | 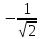 | ( 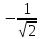 ; ;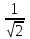 ) ) | 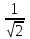 | ( 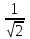 ;+∞) ;+∞) |
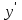 | − | 0 | + | 0 | − |
| у | 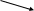 | min | 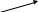 | max | 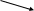 |
-
Выпуклость и точки перегиба. Вычислим вторую производную
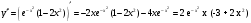
Найдем точки перегиба
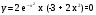 при х=0 и х=
при х=0 и х=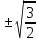
| х | (-∞; 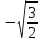 ) ) | 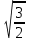 | ( 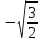 ;0) ;0) | 0 | ( 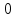 ; ;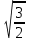 ) ) | 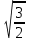 | ( 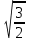 ;+∞) ;+∞) |
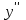 | - | 0 | + | 0 | - | 0 | + |
| у | выпукла | 0 | вогнута | 0 | выпукла | 0 | вогнута |