6. 
   наклонные асимптоты вида у=kx+b
   

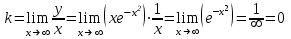
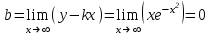
Прямая у=0 – горизонтальная асимптота

7 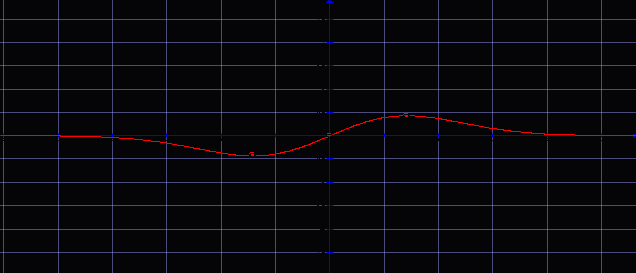. Строим график функции:

Б) На отрезке [-2;2]находятся две точки экстремума х= , функция может достигать наибольшего значения на концах отрезка и в точках экстремума.

у(2)= 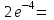0,036631

у(-2)= 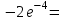-0,036631

у( )= 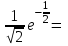0,428882 -максимальное значение на отрезке [-2;2]

у(- )= 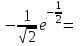-0,428882 -минимальное значение на отрезке [-2;2]

7.9. Найдите производные 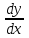данных функций.

Решение:

а)



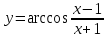
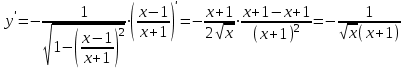
б)



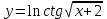
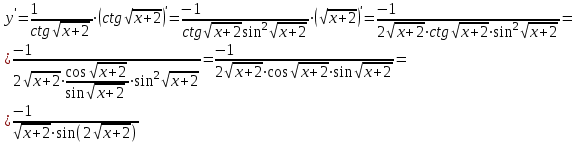
в)







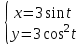
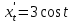
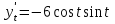
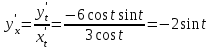
Ответ:

а)

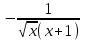
б)

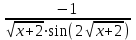
в)

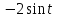
8.9 Найти неопределенные интегралы. Результат проверить дифференцированием.

Решение:

А)

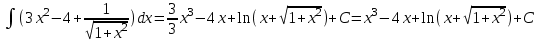
Проверим результат дифференцированием:

---

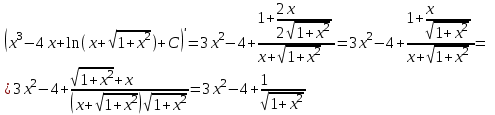
Б)

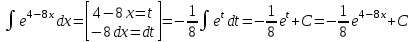
Проверим результат дифференцированием:



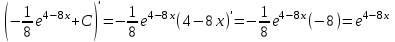
В)



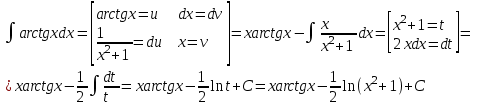
Проверим результат дифференцированием:



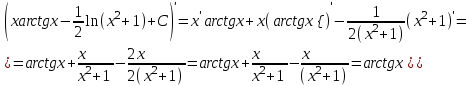
г)

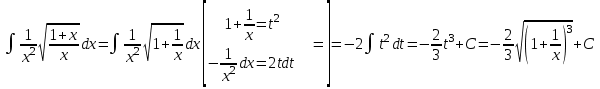
Проверим результат дифференцированием:



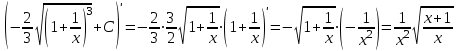
Ответ:

А)

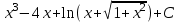
Б)

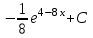
В)

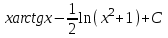
Г)

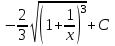
8.9 Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.



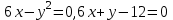
_{Решение:}

Сделаем чертеж.



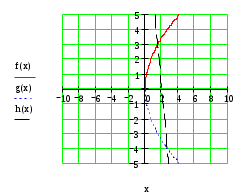
Найдем точки пересечения из решения системы уравнений:





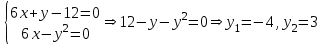
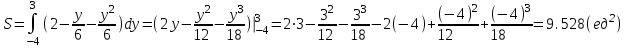
Ответ: 9.528 (ед2)

9.9 Даны функция 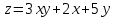и точка М(1,04;2,96). С помощью полного дифференциала вычислить приближенно значение функции в данной точке. Вычислить точное значение функции в точке М₀ и оценить относительную погрешность вычислений.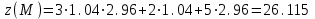



Будем рассматривать z(М) как частное значение функции 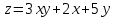при x = 1,04 = x₁, у =2,96 = у₁. За x₀ принимаем число 1, за у₀ –число 3.

Тогда z(x₀,y₀) = ;

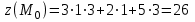Переведём dx в радианы:

dx = x₁ – x₀ = 1,04-2=0,04,

dy = y₁ –y₀ =2,96-3=-0,04

---

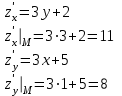
Тогда получим:

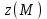 z(x₀,y₀) + 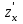(x₀,y₀)dx+ 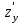(x₀,y₀)dy=26+11*0.04+8*(-0.04)=26,12

Оценим погрешность: %

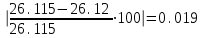Список использованной литературы

1. 
   Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисление. – Т.1. –М.: Дрофа, 2007.
   
2. 
   Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения, кратные интегралы. Ряды. Функции комплексного переменного. – Т.3. – М.: Дрофа, 2005.
   
3. 
   Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. – Т. 1,2. – М.: Высшая школа,2002 .
   
4. 
   Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. – М.: Высшая школа, 2001.
   
5. 
   Лисичкин В.Т., Соловейчик И.Л. Математика. - Москва.: Высшая школа, 1991.
   
6. 
   Германова Е.Н. Высшая математика (дополнительный учебный материал). - Москва.: Связь, 1970.
   
7. 
   Зайцев И.Л. Элементы высшей математики. - Москва.: Наука, 1972.
   
8. 
   Богомолов Н.В., Сергиенко Л.Ю. Сборник дидактических заданий по математике. - Москва.: Высшая школа, 1987.
   

---

Смотрите также файлы

• Конкурс подчеркивает роль дизайниндустрии как драйвера развития инновационных, высокотехнологичных и производственных проектов, демонстрирует связь исследований,.pdf

• .docx

• Роль формальных и неформальных отношений в управлении персоналом оао.pdf

• Как поддерживать оптимальные температурные режимы при экструзии полимерных материалов с большим диссипативным тепловыделением Какие меры необходимо осуществить при изготовлении изделий на экструдерах с диаметром шнека больше 120мм,.docx

• Сопроводительное письмо. Чащина Полина Викторовна.docx