ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТАФедеральное государственное образовательное учреждениевысшего образования«Уральский государственный университет путей сообщения»(УрГУПС)Кафедра «Естественнонаучные дисциплины»Курсовая работапо дисциплине «Маематическое моделирование систем и процессов»Проверил: Выполнил:Профессор студент гр. ЭД 218 (з) Румянцев С.А. Николаев Р. И. Екатеринбург 2019 Вариант 18Задание № 1.

x	1	2+0,1·n	5	7	8
y	2	5	3	4	5+0,1·n

Для заданной табличной функции, где n – номер студента в списке группы, выполнить следующее:1. Построить интерполяционный многочлен (Лагранжа или Ньютона по выбору).2. Для построенного многочлена найти все корни и все экстремумы с точностью ε = 0,001, используя итерационный метод по выбору.3. Построить график многочлена.Решение.Функция 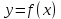задана таблицей:

x	1	3,8	5	7	8
y	2	5	3	4	6,8

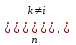
Для неравноотстоящих узлов используем интерполяционную формулу Лагранжа.Формулу Лагранжа можно представить в виде:P_n(x)=Запишем формулу для интерполяционного многочлена в форме Лагранжа.

---

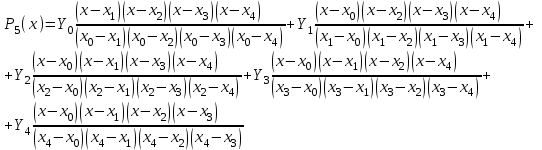
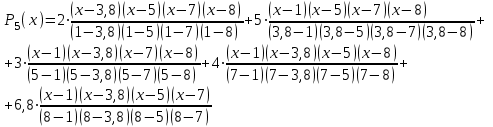
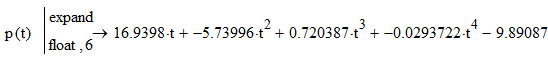
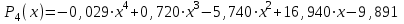
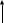
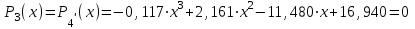
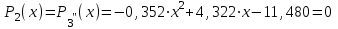
И подставим туда табличные значения:И преобразуем выражение, полученное в среде Mathcad:Интерполяционный многочлен Лагранжа имеет вид:Построим график: у хНайдем экстремумы полученного многочлена численно.Найдем 1-ю производную:Найдем 2-ю производную:Протабулируем функцию 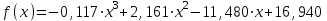в интервале [0; 12] (интервал берем исходя из графика), чтобы отделить корни:Уравнение 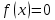имеет три корня: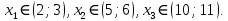 При переходе через точк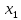и и 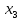функция 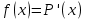меняет знак с «+» на «-», значит, 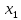и 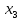– точки максимума; при переходе через 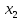функция 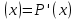меняет знак с «-» на «+», значит, 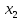– точка минимума.Уточним корни в среде Mathcad:

---

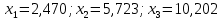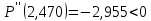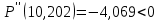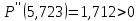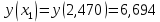
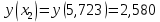
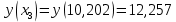
Тогда: . , график выпуклый, – локальный максимум функции; , график выпуклый, – локальный максимум функции; , график вогнутый, – локальный минимум функции.Найдем значения у в точках экстремума:Найдем корни полученного многочлена численно (при у = 0). Протабулируем функцию 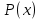в интервале [0; 13] (интервал берем исходя из графика), чтобы отделить корни.Уравнение 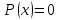имеет 2 корня: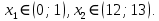 При 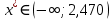функция монотонно возрастает, других корней, кроме , на интервале 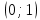быть не может.При 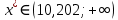функция монотонно убывает, на 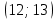один корень .Уточним корни в среде Mathcad:Видим, что действительных корня два: 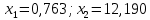.Ответ: интерполяционный многочлен Лагранжа имеет вид:

---

;

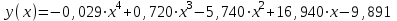
корни данного уравнения: (0,763; 0) и (12,190; 0);

точки экстремума:

(5,723, 2,580) – точка локального минимума функции;

(2,470; 6,694) и (10,202; 12,257) – точки локального максимума функции.

Задание №2. По результатам наблюдений, проведенным на железнодорожной станции, составлена таблица зависимости времени расформирования составов на сортировочной горке от числа вагонов в составе.

Требуется найти зависимость времени расформирования 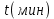от числа вагонов 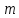в составе в виде двух формул: 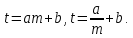Вычислить среднеквадратичные уклонения и выбрать наиболее подходящую эмпирическую формулу. Построить на одном чертеже графики эмпирических зависимостей вместе с точками исходной таблицы.

Решение

Исходные данные варианта 18:

m	20	24	28	32	36	40	44	48	52	54
t	11,8	13,4	14,6	15,9	17,1	18,2	19,3	20,1	21,5	23,4

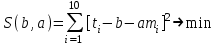
а) прямая t = am+b.Найдем два неизвестных параметра (b, a). 1. Т.к. зависимость линейная преобразования не требуются.2. Найдем методом наименьших квадратов коэффициенты в линейной зависимости.Продифференцировав функцию S по b и a, получим систему уравнений:

---

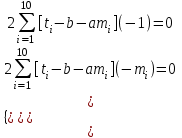
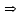
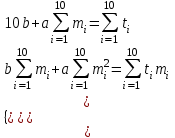
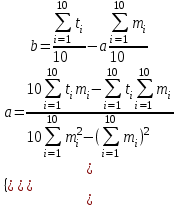
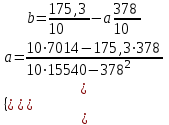
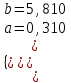
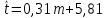
Т.о. 3. Найдем уклонения эмпирической зависимости от значений исходной таблицы ε_i= f(m) – y_i, i= 1,2 .., 10.

№ п/п	m	t	tm	m2	t̂	εi	ε2
1	20	11,8	236	400	12,01	-0,211	0,045
2	24	13,4	321,6	576	13,25	0,149	0,022
3	28	14,6	408,8	784	14,49	0,109	0,012
4	32	15,9	508,8	1024	15,73	0,168	0,028
5	36	17,1	615,6	1296	16,97	0,128	0,016
6	40	18,2	728	1600	18,21	-0,012	0,000
7	44	19,3	849,2	1936	19,45	-0,152	0,023
8	48	20,1	964,8	2304	20,69	-0,593	0,351
9	52	21,5	1118	2704	21,93	-0,433	0,187
10	54	23,4	1264	2916	22,55	0,847	0,718
сумма	378	175,3	7014	15540	175,3	0,000	1,403

---

Смотрите также файлы

• Шкала личностной тревожности (А. М. Прихожан).docx

• Викторина Масаты Оырмандарды ертегілерді білу арылы ойлау, сйлеу абілетін йлесімді дамыту.docx

• бекітемін Талар ауданы кіміні орынбасары А. Бидаев.docx

• Природа и человек в художественной литературе 4.docx

• Хабарлама 2023ж.docx