4. Вычислим среднеквадратичное уклонение:


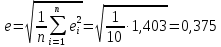
б) гипербола ;

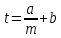Найдем два неизвестных параметра (b, a).

1. Перейдем с помощью преобразования 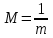от заданной нелинейной зависимости к линейной 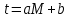. Используя исходную таблицу с данными m_i , t_i составим для неё таблицу значений M_i , t_i для линейной зависимости.

№ п/п	М	t	tМ	М2
1	0,05	11,8	0,59	0,0025
2	0,042	13,4	0,558	0,0017
3	0,036	14,6	0,521	0,0013
4	0,031	15,9	0,497	0,0010
5	0,028	17,1	0,475	0,0008
6	0,025	18,2	0,455	0,0006
7	0,023	19,3	0,439	0,0005
8	0,021	20,1	0,419	0,0004
9	0,019	21,5	0,413	0,0004
10	0,019	23,4	0,433	0,0003
сумма	0,293	175,3	4,801	0,0095

---

2. Найдем методом наименьших квадратов коэффициенты в линейной зависимости.


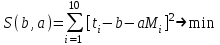
Продифференцировав функцию S по b и a , получим систему уравнений:




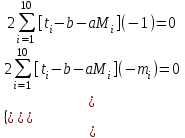
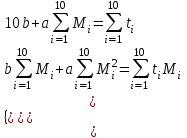
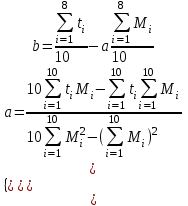
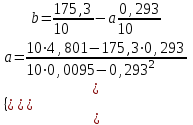
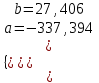
Т.о. t=-337,394M+27,406
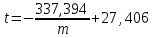
3. Найдем уклонения эмпирической зависимости от значений исходной таблицы ε_i = f(m) – y_i, i= 1,2 .., 10.

№ п/п	t̂	εi	ε2
1	10,54	1,264	1,597
2	13,35	0,052	0,003
3	15,36	-0,756	0,572
4	16,86	-0,963	0,927
5	18,03	-0,934	0,873
6	18,97	-0,771	0,595
7	19,74	-0,438	0,192
8	20,38	-0,277	0,077
9	20,92	0,582	0,339
10	21,16	2,242	5,026
сумма	175,3	0,000	10,199

---

4. Вычислим среднеквадратичное уклонение:


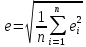
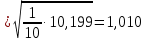
Построим графики эмпирических формул и на этом же чертеже нанесем точки (m_i; t_i) исходной таблицы.

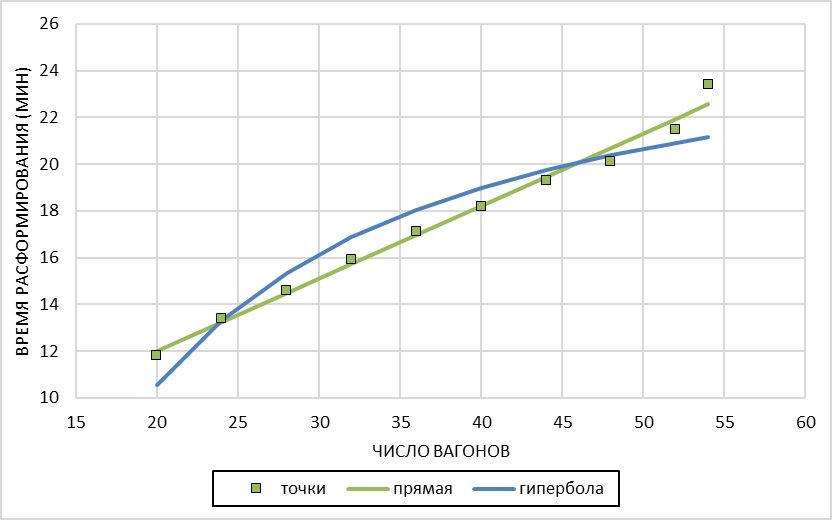
Среднеквадратические отклонения по моделям:

линейная модель = 0,375

гипербола = 1,010
Видим, что среднеквадратичное уклонение у прямой меньше, чем у гиперболы, значит наиболее подходящая эмпирическая формула для описания зависимости времени расформирования составов на сортировочной горке от числа вагонов в составе имеет вид:

---

Смотрите также файлы

• Шкала личностной тревожности (А. М. Прихожан).docx

• Викторина Масаты Оырмандарды ертегілерді білу арылы ойлау, сйлеу абілетін йлесімді дамыту.docx

• бекітемін Талар ауданы кіміні орынбасары А. Бидаев.docx

• Природа и человек в художественной литературе 4.docx

• Хабарлама 2023ж.docx