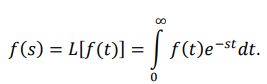Файл: Метод.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 22.11.2023

Просмотров: 21

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

(ФГБОУ ВО «АмГУ»)

Факультет Математики и информатики

Кафедра Информационных и управляющих систем

Направление подготовки 09.03.01 «Информатика и вычислительная техника»


ЛАБОРАТОРНАЯ РАБОТА № 1

Тема: Метод пространства состояний

Номер варианта: 5


Исполнитель

Студент группы 053-об (подпись, дата)


А.Е. Калинин


Руководитель

профессор, д.т.н. (подпись, дата)



Е. Л. Еремин



Благовещенск 2023

Цель: изучение понятия пространства состояния и способа прямого программирования.



Выполнение работы:
  1. В соответствии с вариантами заданий, с помощью прямого преобразования Лапласа запишите передаточную функцию соответствующего дифференциального уравнения.

В соответствии с вариантом представлены следующие исходные данные: ????1=1 и ????2=2.3 k=1. Рассматриваемое дифференциальное уравнение имеет следующий вид:



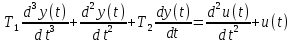
Пользуясь прямым преобразованием Лапласа, приведем ДУ к следующему виду:



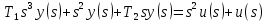
Применим алгебраические преобразования:




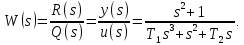
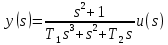
  1. На основании полученного в п.1 результата, используя метод прямого программирования, представьте ее математическое описание исследу емой функции в векторно-матричном виде, записав при этом все необходи мые числовые значения матриц и векторов.

Переведем уравнение в векторно-матричную форму методом прямого программирования:



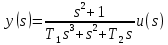
  1. Разделим числитель и знаменатель функции W(s)на слагаемое с максимальной степенью sв знаменателе (в данном случае – это ????1????3), в результате получим уравнение:



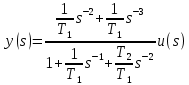
2) Введем в рассмотрение дополнительное обозначение



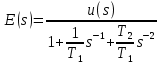
3) перепишем последнее уравнение эквивалентным образом



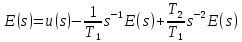
4) запишем уравнение



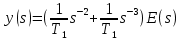
5) введем в рассмотрение изображения переменных состояния и запишем уравнения:





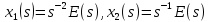
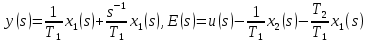
6) в результате, объединяя полученные уравнения, находим:



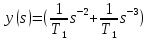
в векторно-матричной форме записи, имеющие следующий вид:





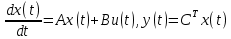
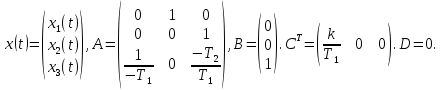
Подставим значения T1=1 T2=2.3.


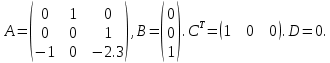
  1. Используя программную среду MATLAB, задайте передаточную функцию, полученную в п.1, путем ввода ее числителя и знаменателя; получите векторно-матричное описание передаточной функции с помощью встроенного оператора MATLAB tf2ss.

Построим листинг файла, вычисляющего параметры векторно-матричной формы записи:

T1=1; T2=2.3;

n=[1 0 0];

d=[T1 T2 0 1];

[A,B,C,D]=tf2ss(n,d)
Результат работы представлен на рисунке 1.



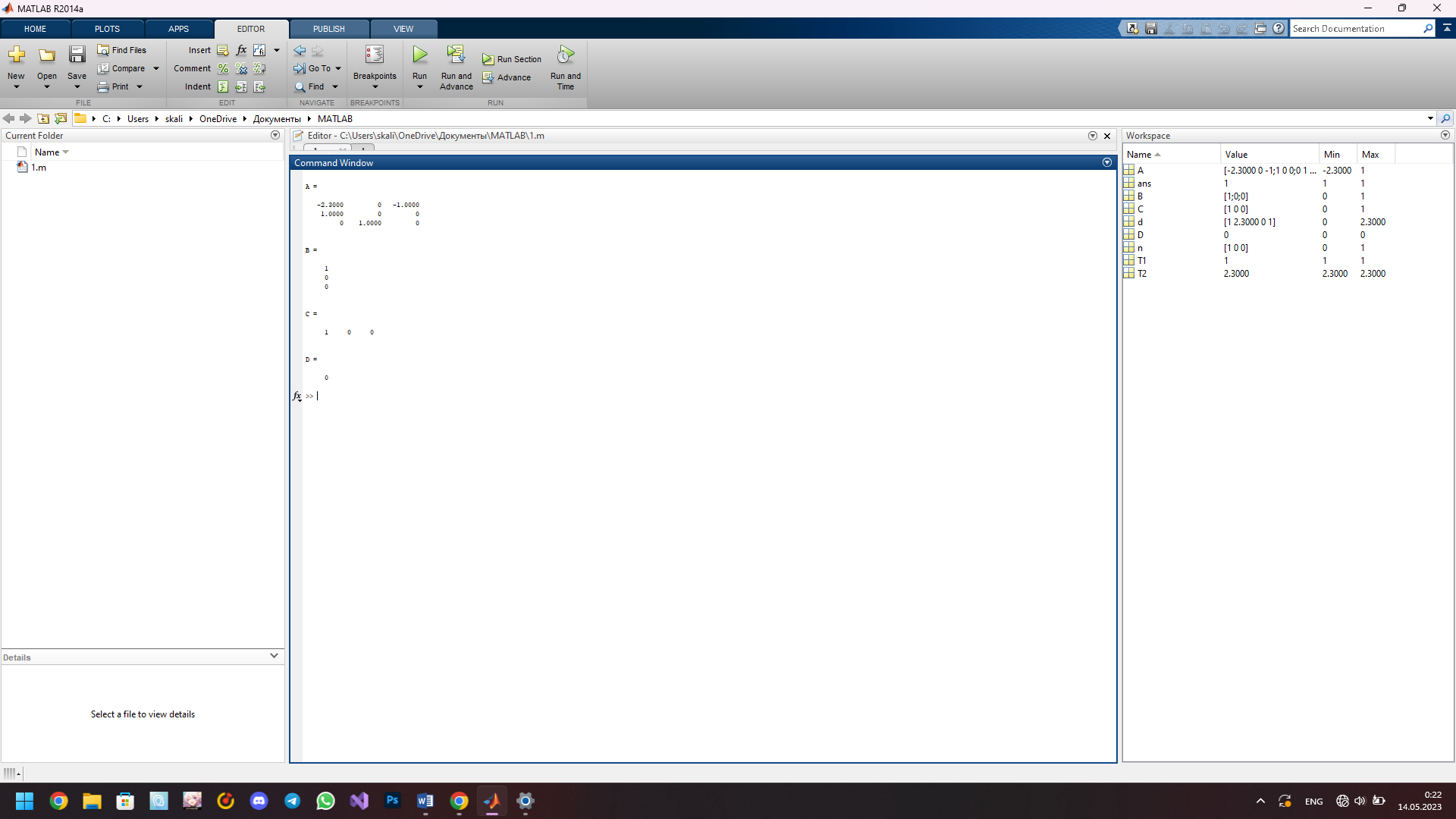
Рисунок 1 – Результат работы файла
  1. Сравните числовые значения матриц и векторов передаточной функции, полученные аналитическим и программным способом.

Как можно увидеть, значения векторов и матриц передаточной функции, полученных аналитическим способом:



и программным способом (рис.1) имеют одинаковые числовые значения, однако  эти значения как бы «отзеркалены» по вертикали. Т.е. третья строка матрицы A, полученная аналитически, соответствует первой строки матрицы A, полученной в Matlab. И при этом значения по столбцам записаны задом наперед. Т.е., например, та же строка, полученная аналитически выглядит так: -1, 0, -2.3. А в Matlab эта строка выглядит иначе: -2.3, 0, -1.

  1. Используя преобразование Лапласа, получите вторую стандартную форму записи в векторно-матричном виде.

Определим уравнение



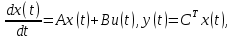
Определим векторно-матричный аналог второй формы записи.



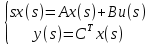
Выполним ряд преобразований над уравнением системы







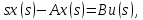
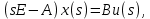
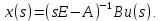
где ???? – единичная матрица соответствующего размера.

Подставим полученное выражение во второе уравнение системы, и получим выражение передаточной функции в векторно-матричной форме:






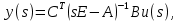
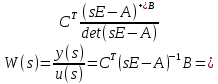
где (???????? − ????) равно:



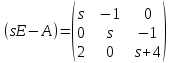
Тогда (???????? − ????)+ – присоединенная матрица и ????????????(???????? − ????) – определитель матрицы будут равны:



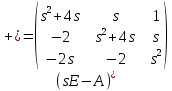
????????????(???????? − ????) = s3+4????2 + 2

Тогда 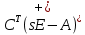будет равна: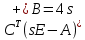



В этом случае передаточная функция ????(????) будет равна:



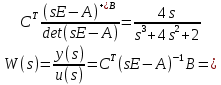
  1. Подставьте числовые значения матриц в выражение, полученное в п.5 и получите выражение передаточной функции. Сравните результат с передаточной функцией из п.1.

Передаточная функция, полученная из предыдущего пункта, с подставленными числовыми значениями выглядит следующим образом:



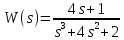
Передаточная функция, полученная в пункте 1, выглядит следующим образом:



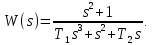
Где ????1=1 и ????2=2.3.

Разница в коэффициентах отличается в 2 раза, так как числитель и знаменатель были разделены на Т2.

  1. С помощью оператора MATLAB ss2tf переведите полученное в п.3 векторно-матричное описание исследуемой функции в эквивалентную запись в виде числителя и знаменателя передаточной функции.

T1=1; T2=2.3;

n=[1 0 0];

d=[T1 T2 1];

[A,B,C,D]=tf2ss(n,d);

pause;

[nn,dd]=ss2tf(A,B,C,D);
Результат выполнения программы представлен на рисунке 2.



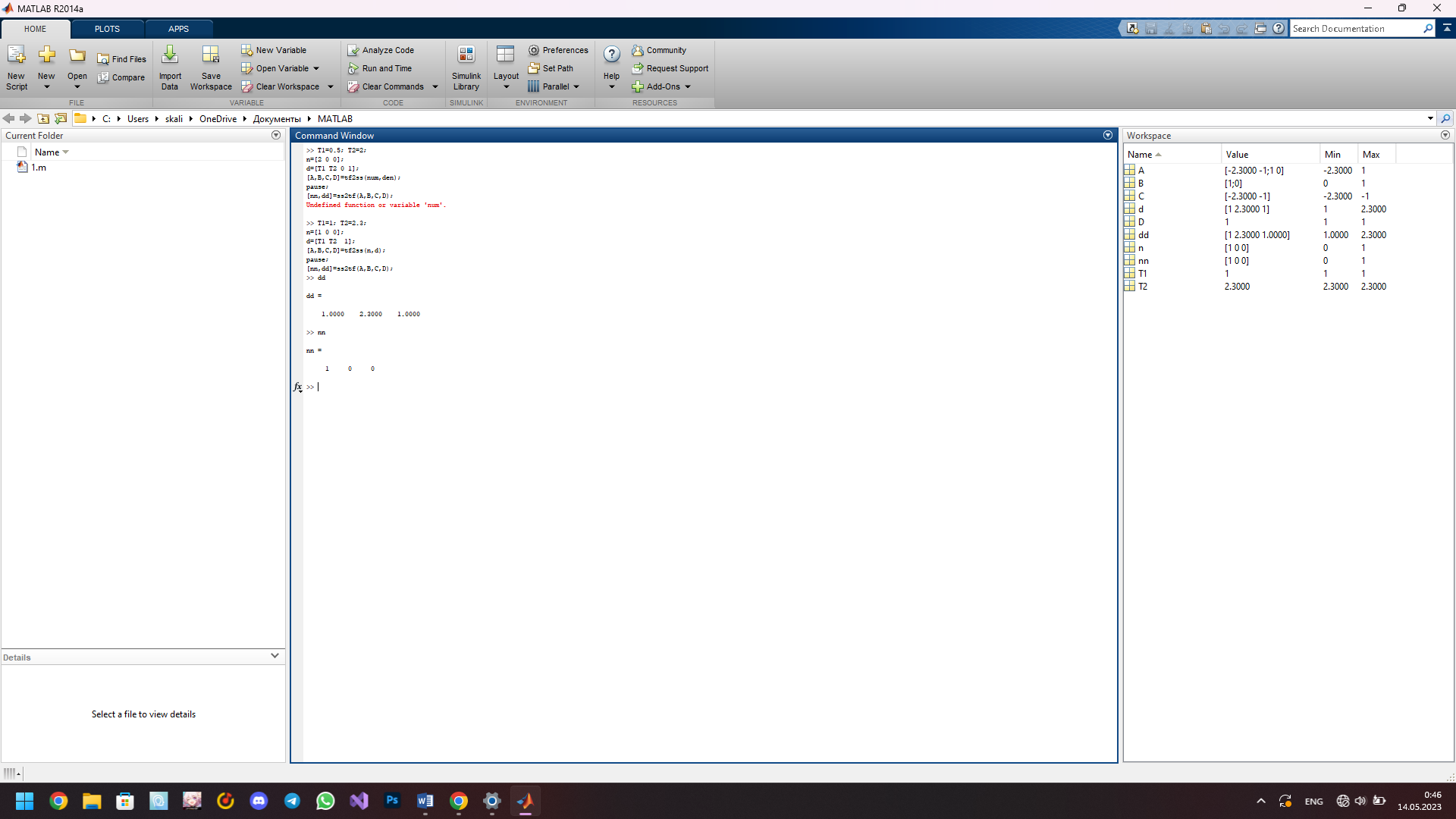
Рисунок 2 - Числитель и знаменатель передаточной функции


  1. Сравните полученный результат с результатами, полученными в п.1 и п.6.

Результат полностью совпадает с передаточной функцией из п.6 и равен передаточной функции из п.1, в которой и числитель и знаменатель были бы разделены на ????1. В результате лабораторной работы было получено векторноматричное описание САУ. Произведен сравнительный анализ данный полученных аналитическим путем и расчётов в математическом пакете MATLAB.


Контрольные вопросы

  1. Раскройте сущность понятия «пространство состояний». Пространство состояний – это метрическое пространство, каждый элемент которого полностью определяет состояние рассматриваемой динамической системы (процесса) в каждый конкретный момент времени. Пространство состояний применяется при описании замкнутых систем, которые не взаимодействуют с другими системами и внешней средой, так и для описания систем, в которых имеет место указанное взаимодействие.

  2. Перечислите известные типовые формы записи математического описания САУ. Приведите примеры. В первой форме записи выходная переменная y(t) и все ее производные записываются в левой части ДУ, причем сама выходная переменная y(t) должна входить в уравнение с коэффициентом, равным 1. Все входные переменные и их производные записываются в правой части уравнения. Пример дифференциального уравнения третьего порядка



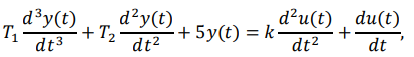
где T1, T2, k – некоторые постоянные коэффициенты; y(t)∈R 2 – выходной сигнал объекта; u(t)∈R – скалярный вход объекта. Вторая форма записи опирается на использование интегральных преобразований Лапласа с применением аппарата передаточных функций. Прямое преобразование Лапласа служит для преобразования функции действительной переменной t (оригинал) в функцию комплексной переменной s (изображение). Если применить преобразование Лапласа к дифференциальному уравнению, приведенному выше, можно получить следующее уравнение



  1. Дайте строгое определение передаточной функции. Передаточная функция – результат отношения выходного сигнала к входному сигналу, записанный в форме преобразований Лапласа при нулевых начальных условиях. Знаменателем передаточной функции называют характеристическим уравнением.

  2. Преобразование Лапласа. Изображение производной. Прямое преобразование Лапласа служит для преобразования функции действительной переменной t (оригинал) в функцию комплексной переменной s (изображение).

Смотрите также файлы