ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
С помощью интегрального преобразования Лапласа относительно действительной переменной t линейное ДУ преобразуется в алгебраическое линейное уравнение, за-писанное относительно комплексной переменной s, при этом, получение изображения интересующего сигнала является вполне очевидным: ????(????) → ????(????).
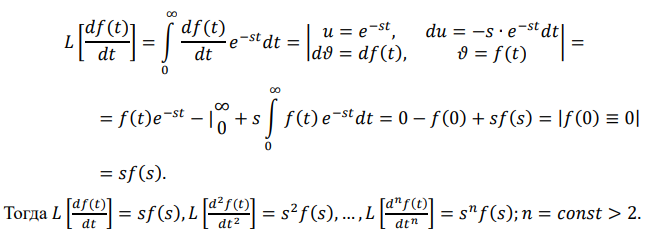
-
Как получить форму записи динамики САУ в виде передаточной функции, если первоначально известно определяющее ее свойства дифференциальное уравнение? Чтобы получить запись динамики САУ в виде передаточной функции, необходимо подвергнуть ДУ интегральному преобразованию Лапласа. В результате должно появиться следующее выражение
С помощью алгебраических преобразований полученное уравнение преобразуется к виду
где ????(????) – передаточная функция, которая всегда представляет отношение некоторых полиномов ????(????) и ????(????) соответствующих порядков и в данном конкретном случае имеет вид
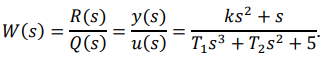
Тогда уравнение примет вид
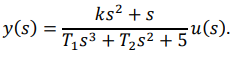
6. Как аналитически можно получить векторно-матричное описание САУ? Для аналитического проектирования САУ различного назначения, как правило, используется их описание в типовой форме вида.
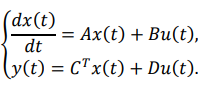
Для перевода стандартной формы записи в векторно-матричную форму записи широкое распространение получил метод прямого программирования.
7. Перечислите типовые шаги применения метода прямого программирования. Приведите пример.
Переведем уравнение
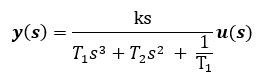
-
Разделим числитель и знаменатель функции W(s)на слагаемое с максимальной степенью sв знаменателе (в данном случае – это ????1????2), в результате получим уравнение:
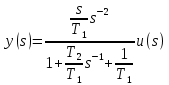
1) Введем в рассмотрение дополнительное обозначение
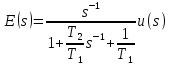
2) перепишем последнее уравнение эквивалентным образом
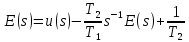
3) запишем уравнение
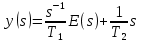
4) введем в рассмотрение изображения переменных состояния и запишем уравнения:

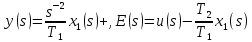
5) в результате, объединяя полученные уравнения, находим:
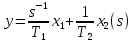
6) подставим значения T1=0.5 T2=2.
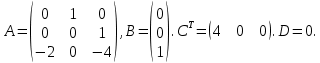
8. Как с помощью программной среды MATLAB возможно получение математической записи динамики системы в пространстве состояний, а также в виде передаточной функции? Для вычисления числовых значений матриц и векторов канонической формы записи в среде MATLAB предусмотрена встроенная функция tf2ss(num,den), которой в качестве параметров передаются полиномы, определяющие числитель (num) и знаменатель (den) исходной передаточной функции. Результат работы функции – рассчитанные значения матриц состояния, управления, выхода и обхода системы, предоставляющих возможность записи стандартного математического описания в пространстве состояний. Реализация обратной операции, т.е. вычисление коэффициентов полиномов числителя и знаменателя передаточной функции, возможна с использованием встроенной функции ss2tf(A,B,C,D). Данной функции передаются значения векторов и матриц, определяющих параметры системы. Результат работы функции – рассчитанные коэффициенты полиномов числителя и знаменателя передаточной функции.