Министерство образования и науки РФФедеральное государственное бюджетное образовательноеучреждение высшего образования«Алтайский государственный технический университет им. И.И. Ползунова»Заочный институтКафедра Контрольная работа защищена с оценкой_______________________ _________________С. Ф. Нефёдов(подпись преподавателя) (инициалы, фамилия) “___ ”___________ 202_ г.Контрольная работапо дисциплине «Введение в электротехнику» (наименование дисциплины) Вариант 68Студент группы 4Э-91______________________________(инициалы, фамилия)Преподаватель кандидат теxнических наук, доцент___ С. Ф. 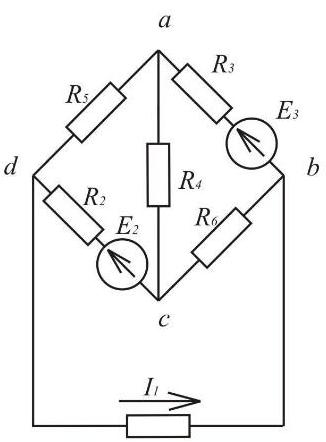Нефёдов(должность, ученое звание) (инициалы, фамилия)БАРНАУЛ 2020Задание 1 Линейные цепи постоянного токаДля электрической схемы, изображенной на рисунке 1, выполнить следующее:Рисунок 11. Составить на основании законов Кирхгофа систему уравнений для нахождения токов во всех ветвях схемы. 2. Определить токи во всех ветвях схемы методом контурных токов.3. Определить токи во всех ветвях схемы методом узловых потенциалов. 4. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить их между собой. 5. Составить баланс мощностей в расчетной схеме, вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). 6. Определить ток I₁, в заданной по условию схеме, используя теорему об активном двухполюснике и эквивалентном генераторе.7. Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе э.д.с.Исходные данные:R₁=12 Ом; R₂=10 Ом; R₃=16 Ом; R₄=28 Ом; R₅=14 Ом; R₆=16 Ом; E₂=40 В; E₃=12 В.Решение1. Заданная схема содержит n=6 неизвестных токов (I₁, I₂, …, I₆) и m=4 узла (a,b,c,d). Составляем k=m-1=3 уравнения по 1-му закону Кирхгофа и n-k=3 уравнения по 2-му закону Кирхгофа.

---

Задаем направления токов в ветвях, направления обхода контуров I, II, III, и составляем систему уравнений (рисунок 2).



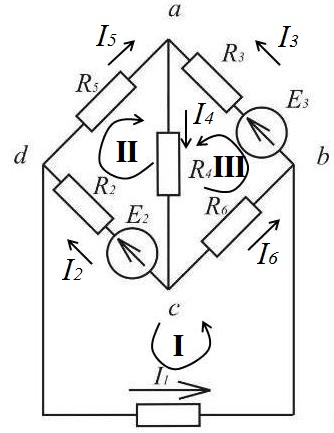
Рисунок 2



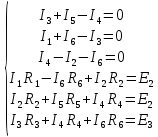
2. Расчет методом контурных токов.

Для выбранных контуров I, II, III обозначаем контурные токи как I₁₁, I₂₂, I₃₃ и составляем систему уравнений по методу контурных токов.





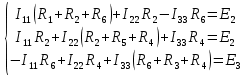
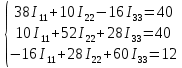
Решаем систему уравнений и определяем значения контурных токов:







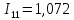
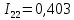
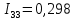
Определяем значения токов в ветвях













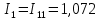
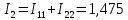
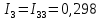
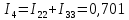
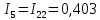
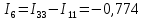
3. Расчет методом узловых потенциалов.

Принимаем потенциал узла d φ_d=0 В, составляем и решаем систему уравнений по методу узловых потенциалов для остальных узлов.





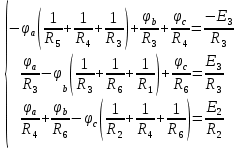
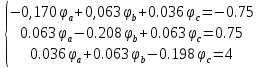
Решаем систему уравнений и определяем потенциалы узлов цепи







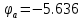
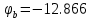
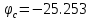
Определяем токи в ветвях

---

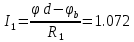
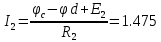
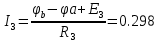
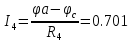
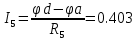
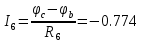
4. Составляем сравнительную таблицу.

Ток, А	I1	I2	I3	I4	I5	I6
Метод контурных токов	1.073	1.475	0.298	0.700	0.403	-0.774
Метод узловых потенциалов	1.073	1.475	0.298	0.700	0.403	-0.774

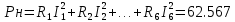
Как видно из таблицы, обоими методами получены одинаковые значения токов в ветвях. 5. Составляем баланс мощностей для исходной схемы.Мощность источниковР_ист = Е₂I₂ + Е₃I₃ = 58.990 + 3.577= 62.567Мощность нагрузокPн = Баланс мощностей сходится.6. Расчет методом эквивалентного генератораОпределяем напряжение холостого хода на разомкнутых зажимах b и d. 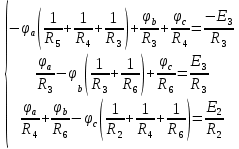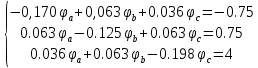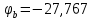Для расчета используем метод узловых потенциалов.Систему уравнений решаем Определяем потенциал узла b цепиЗначение напряжения холостого хода на разомкнутых зажимах d и b:_{U = 27.767}Э.Д.С. эквивалентного генератора:_{E = 27.767}Определяем эквивалентное сопротивление 1-й ветви. Для расчета закорачиваем все идеальные источники э.д.с. 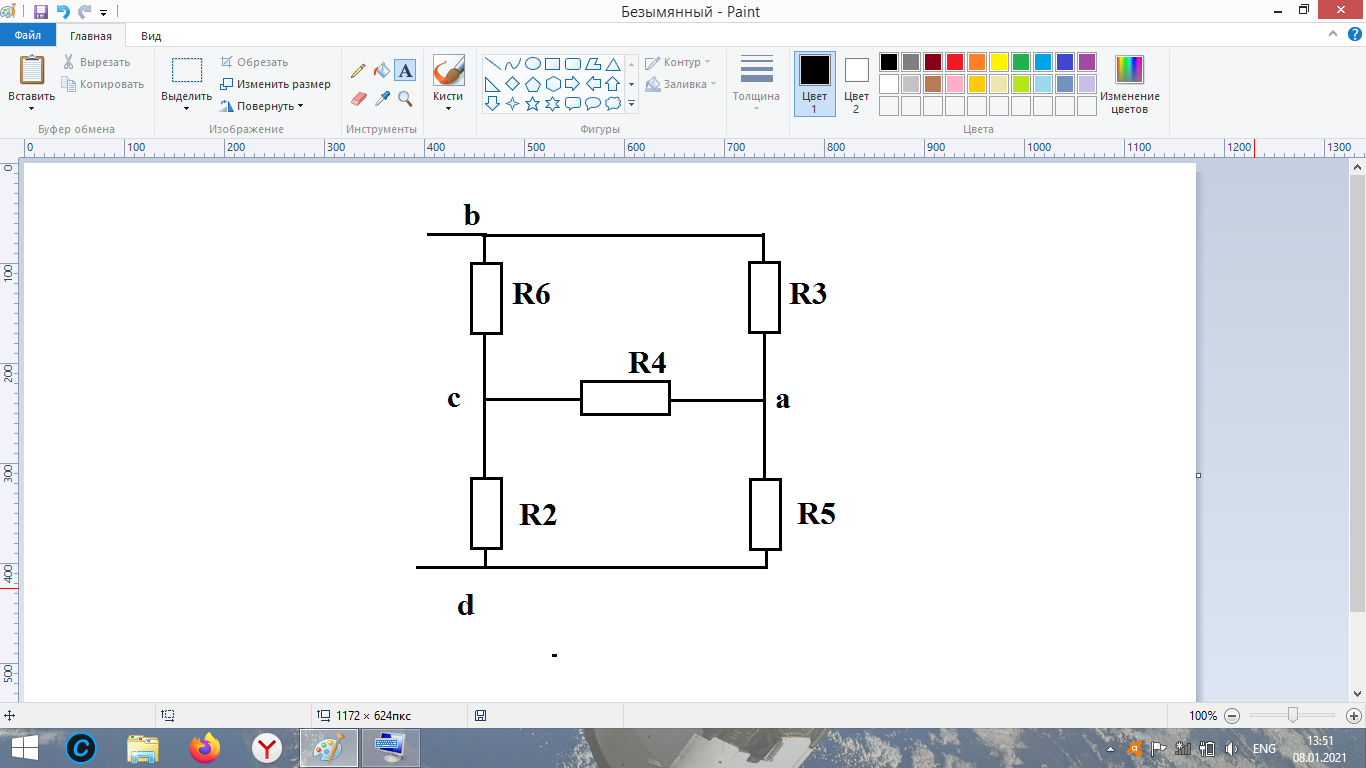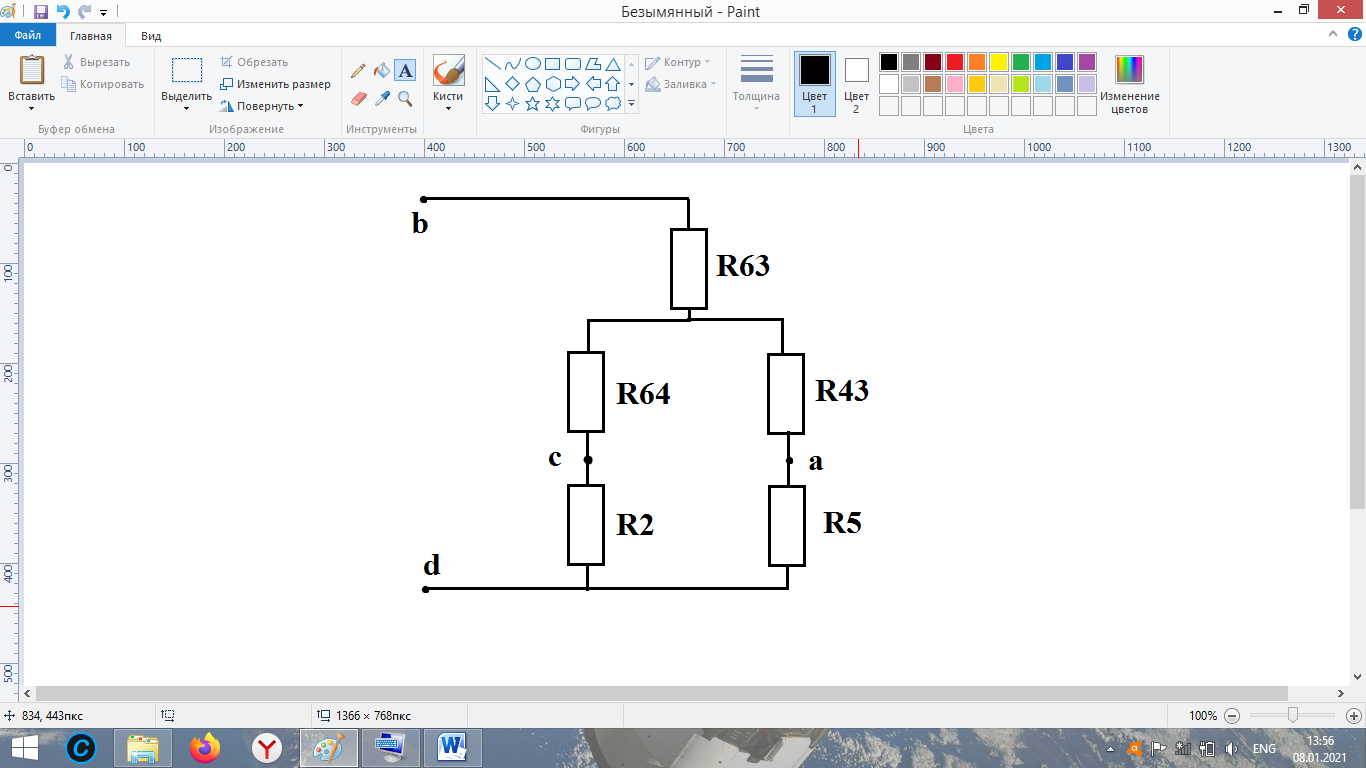и преобразуем треугольник сопротивлений R₆-R₃-R₄ (рисунок 4а) в эквивалентную звезду R₆₃-R₄₃- R₆₄ (рисунок 4б)_.а) б)Рисунок 4

---

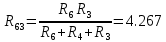
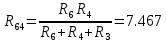
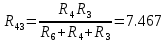
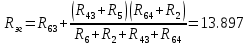
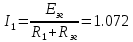
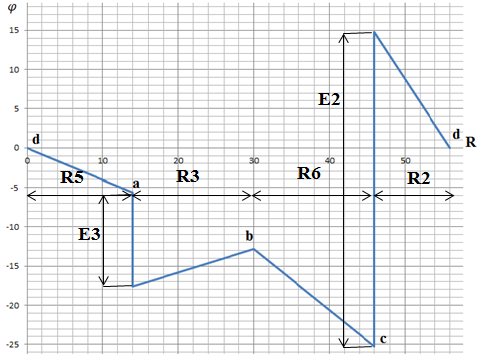
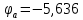
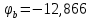
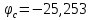
Ток I₁ рассчитываем по формуле7. Для построения потенциальной диаграммы необходимо определить потенциалы точек цепи.Из расчетов по методу узловых потенциалов имеем:По этим значениям строим потенциальную диаграмму контура d-a-b-c-d (рисунок 5).

---

Смотрите также файлы

• Договор аренды в гражданском законодательстве 5 1Понятие договора аренды 5.doc

• Вопросы Предоставьте руководству несколько устройств (не менее 5) для выбора, укажите характеристики.rtf

• Практическая работа 3 Таланты детей Глоссарий.docx

• Российский государственный аграрный университет мсха имени К. А. Тимирязева.pdf

• Энергетический обмен.docx