ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 27
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Группа МАШбп(до)з-18-1
Кузьмин Ю.А.
Вариант 8.
Пример К1. Даны уравнения движения точки в плоскости ху :
x = 6t-3 , y = t3
(х, у - в сантиметрах, t - в секундах).
Определить уравнение траектории точки; для момента времени t1 = 1 c найти скорость и ускорение точки.
Решение. Для определения уравнения траектории точки исключим из заданных уравнений движения время t.
Отсюда находим следующее уравнение траектории точки 6t = x+3 t = (x+3)/6
у = ((х+3)/6)3
Скорость точки найдем по ее проекциям на координатные оси:
Vx =
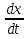 = 6 Vy =
= 6 Vy = 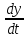 = 3t2 V =
= 3t2 V = 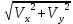
и при t=1 c : V1x = 6 см/c, V1y = 3 см/c, V1 = 6,7 см/c.
Аналогично найдем ускорение точки :
ax =
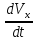 = 0 ay =
= 0 ay = 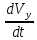 = 6t
= 6t 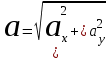
и при t=1 c a1x = 0 см/c2, a1y = 6 см/c2, a1 = 6 см/c2.
Контрольные вопросы
1.Какими способами может быть задано движение точки?
Движение точки может быть задано тремя способами: естественным, векторным и координатным.
Итак, движение точки в рассматриваемом случае определяется совокупностью следующих данных: траектории точки, положения начала отсчета дуговой координаты, положительного и отрицательного направлений отсчета и функции
П
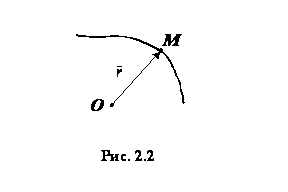 ри векторном способе задания движения точки положение точки
ри векторном способе задания движения точки положение точки 2.Что задается при векторном способе задания движения?
Итак, движение точки в рассматриваемом случае определяется совокупностью следующих данных: траектории точки, положения начала отсчета дуговой координаты, положительного и отрицательного направлений отсчета и функции
П
 ри векторном способе задания движения точки положение точки
ри векторном способе задания движения точки положение точки Это равенство называется векторным уравнением движения точки.
3.Что задается при координатном способе задания движения?
При координатном способе
задания движения положение точки по отношению к выбранной системе отсчета определяется при помощи прямоугольной системы декартовых координат (рис. 2.3). При движении точки ее координаты изменяются с течением времени. Поэтому, чтобы определить положение точки в любой момент времени, достаточно задать координаты
Эти равенства называются уравнениями движения точки в прямоугольных декартовых координатах. Движение точки в плоскости определяется двумя уравнениями системы (2.3), прямолинейное движение — одним.
Между тремя описанными способами задания движения существует взаимная связь, что позволяет от одного способа задания движения перейти к другому. В этом легко убедиться, например, при рассмотрении перехода от координатного способа задания движения к векторному.
4.Что задается при естественном способе задания движения?
При естественном способе задания движения дается траектория, т. е. линия, по которой движется точка (рис.2.1). Н
 а этой траектории выбирается некоторая точка
а этой траектории выбирается некоторая точка Это равенство называется уравнением движения точки по данной траектории.
5.Как находится траектория точки координатном способе задания движения?
В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:
x=x(t)
y=y(t)
z=z(t)
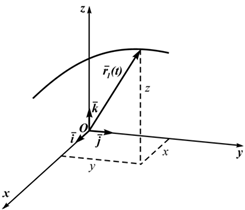 Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.
Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):
6.Как находится скорость и ускорение точки векторном способе задания движения?
Чтобы получить скорость точки в данный момент времени, необходимо совершить предельный переход
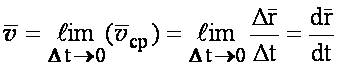 (1.6)
(1.6)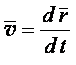 (1.7)
(1.7)Вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора по времени и направлен по касательной к траектории в данной точке.
(единица измерения м/с, км/час)
Ускорение точки при векторном способе задания движения
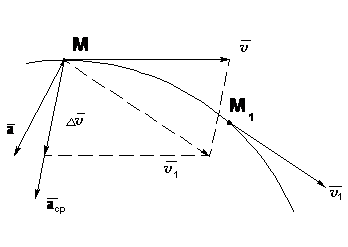 | 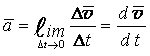 (1.9) (1.9)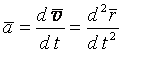 (1.10) (1.10) |
Вектор среднего ускорения имеет то же направление, что и векторΔv, то есть, направлен в сторону вогнутости траектории.
Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
(еденица измерения -
6.Как находится скорость и ускорение точки координатном способе задания движения?
Связь векторного способа задания движения и координатного дается соотношением
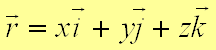 (рис. 6).
(рис. 6). Из определения скорости:
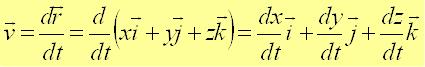 .
.Проекции скорости на оси координат равны производным соответствующих координат по времени
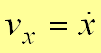 ,
, 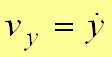 ,
, 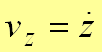 . .
. . Модуль и направление скорости определяются выражениями:
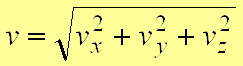 ,
,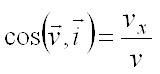
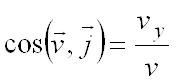
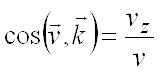 .
.Точкой сверху здесь и в дальнейшем обозначается дифференцирование по времени
Из определения ускорения:
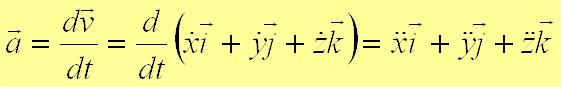 .
.Проекции ускорения на оси координат равны вторым производным соответствующих координат по времени: