ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 28
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 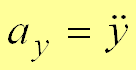 ,
, 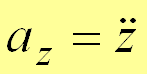 .
.
Модуль и направление ускорения определяются выражениями:
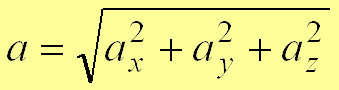 ,
,
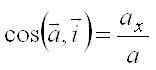 ,
, 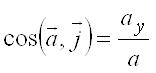 ,
, 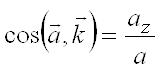 .
.
Как находится скорость и ускорение точки естественном способе задания движения?
Определение скорости и ускорения точки при естественном способе задания движения
Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения. Касательная (с единичным вектором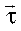 ) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку (рис.9). Через касательную проходит соприкасающаяся плоскость (рис. 10), которая находится как предельное положение плоскости при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали
) направлена по касательной в положительном направлении отсчета дуговой координаты и находится как предельное положение секущей, проходящей через данную точку (рис.9). Через касательную проходит соприкасающаяся плоскость (рис. 10), которая находится как предельное положение плоскости при стремлении точки M1 к точке M. Нормальная плоскость перпендикулярна касательной. Линия пересечения нормальной и соприкасающейся плоскостей − главная нормаль. Единичный вектор главной нормали 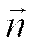 направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором
направлен в сторону вогнутости траектории. Бинормаль (с единичным вектором 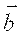 ) направлена перпендикулярно касательной и главной нормали так, что орты
) направлена перпендикулярно касательной и главной нормали так, что орты  ,
, 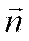 и
и 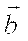 образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который
образуют правую тройку векторов. Координатные плоскости введенной подвижной системы координат (соприкасающаяся, нормальная и спрямляющая) образуют естественный трехгранник, который
перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.
Из определения скорости точки
 ,
,
где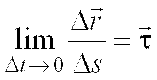 ,
,  − единичный вектор касательной.
− единичный вектор касательной.
Тогда
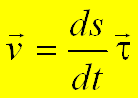 ,
, 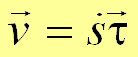 .
.
Алгебраическая скорость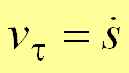 − проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
− проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
Из определения ускорения
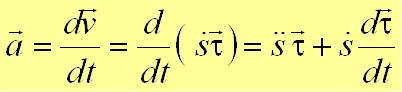 ,
,
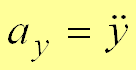 ,
, 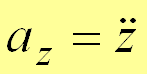 .
.Модуль и направление ускорения определяются выражениями:
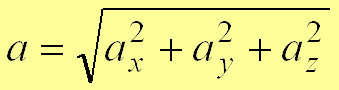 ,
,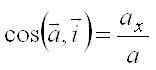 ,
, 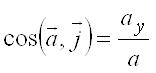 ,
, 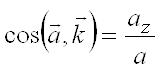 .
.Как находится скорость и ускорение точки естественном способе задания движения?
Определение скорости и ускорения точки при естественном способе задания движения
Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения. Касательная (с единичным вектором
перемещается вместе с движущейся точкой, как твердое тело. Его движение в пространстве определяется траекторией и законом изменения дуговой координаты.
Из определения скорости точки
 ,
,где
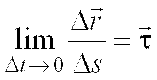 ,
, Тогда
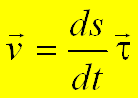 ,
, 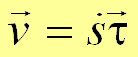 .
.Алгебраическая скорость
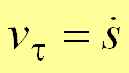 − проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.
− проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты. Из определения ускорения
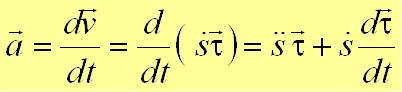 ,
,