Екінші ретті қисықтардың жалпы теңдеуі. Екінші ретті беттердің канондық теңдеуі
п.ғ.м Қанибайқызы Құндызай
Негізгі терминдер:. Екінші ретті қисықтар.. Директрисса. Шеңбер.Эллипс.Гипербола. Парабола

Екінші ретті сызық төмендегі теңдеу арқылы беріледі:

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.
Бұл теңдеу төменде келтірілген теңдеулердің біріне келтірілетіндей координаталар жүйесі (тік бұрышты болуы міндетті емес) болуы мүмкін.

1. Шеңбер дегеніміз – центр деп аталатын 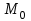нүктесінен радиус деп аталатын 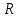қашықтығында жататын барлық нүктелер жиыны.

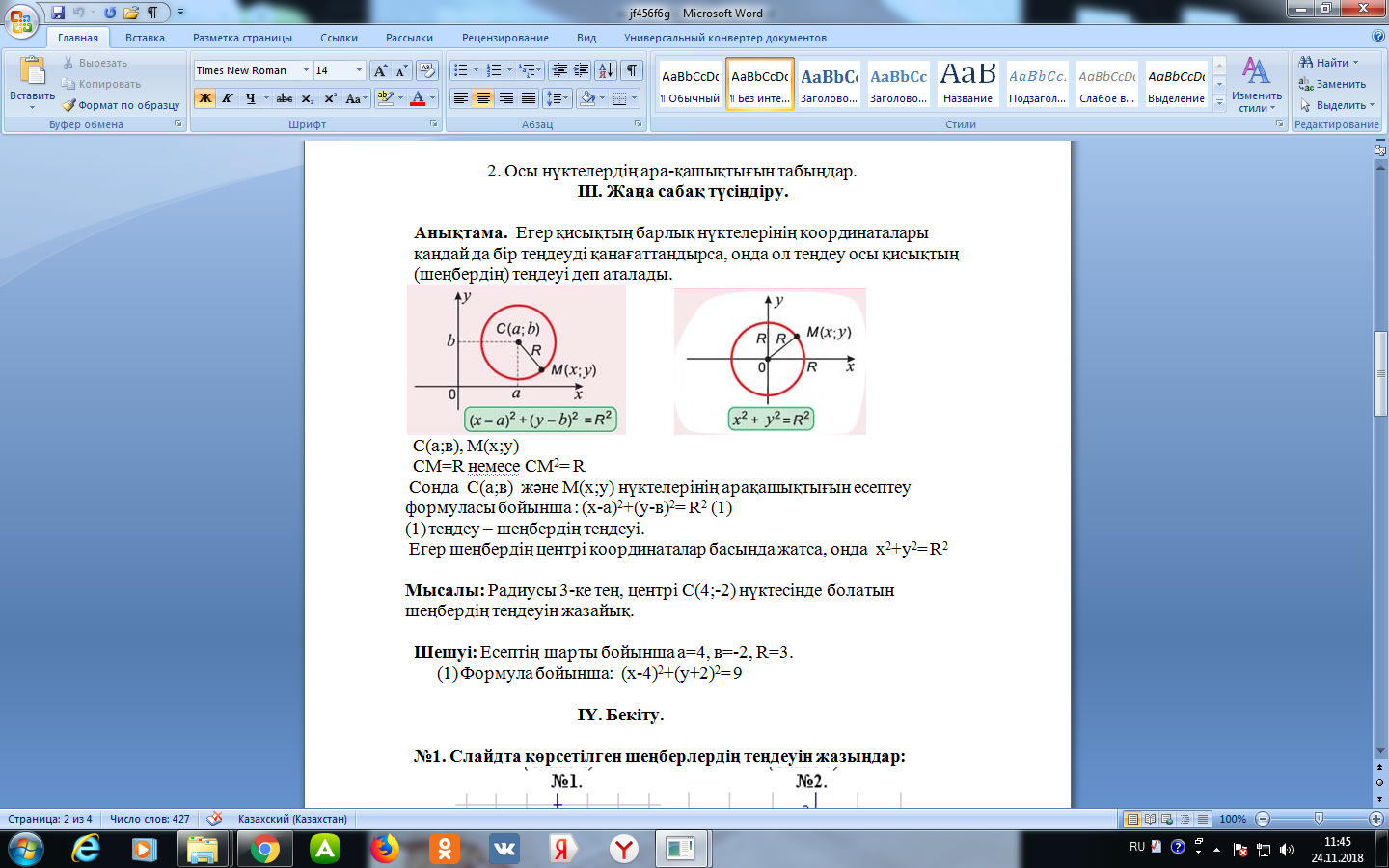Айталық, шеңбердің центрі 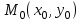, радиусы 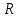және шеңбердің кез келген нүктесі 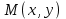берілсін. Анықтама бойынша 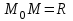. Бұдан екі нүктенің арасындағы қашықтық формуласын пайдалансақ:

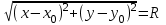немесе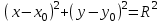

1. 
   формула шеңбердің канондық теңдеуі деп аталады.
   

Егер шеңбердің центрі координата басында жататын болса, онда оның теңдеуі

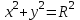түрінде жазылады.

2. Анықтама. Эллипс дегеніміз – фокустар деп аталатын 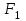және 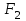нүктелерінен қашықтықтарының қосындысы тұрақты 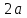санына тең болатын жазықтықтағы нүктелер жиыны.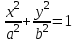



формула эллипстің канондық теңдеуі деп аталады.

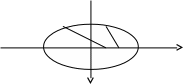у

М

r₁

r₂

---

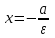
F₁ O F₂



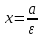
F₁, F₂ – эллипстің фокустары. F₁ = (-c; 0); F₂(c; 0), F₁F₂ = 2c.

Теорема. Эллипстің фокустық ара қашықтығы мен жарты өстері мынадай қатынас бойынша байланысады:

a² = b² + c².
Мұндағы, .

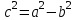с – фокустары ар қашықтығының жартысы; 2а - тұрақты шама.

- эллипстің үлкен жарты осі;

- эллипстің кіші жарты осі.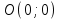

нүктесі – эллипстің центрі.

Фокустың координаталары 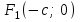және 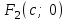болады.

Фокустар арақашықтығының үлкен ось ұзындығына қатынасы:



эллипстің эксцентриситеті деп аталады.

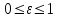Эксцентриситет эллипстің сығылу дәрежесін анықтайды.

2. 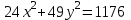эллипстің теңдеуі берілген.

а) жарты осьтерінің ұзындығын;ә) фокустарының координаттарын;б) эллипстің эксцентриситетін табу керек.

▼ Екі жағын 1176-ға бөліп, эллипстің канондық теңдеуіне келтіреміз: .

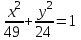а) 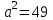, , 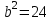яғни , .

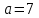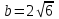ә) 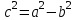формуласы бойынша, 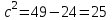, 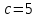. Бұдан , .

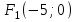б) Формула бойынша

---

. ▲

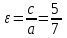
3.Гипербола дегеніміз - фокустар деп аталатын және нүктелерінен қашықтықтарының айырмасы тұрақты санына тең болатын жазықтықтағы нүктелер жиыны.

2. 
   формула гиперболаның канондық теңдеуі деп аталады.
   

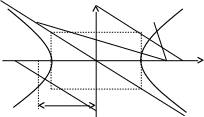
F₁, F₂ – гиперболаның фокустары. F₁ = (-c; 0); F₂(c; 0), F₁F₂ = 2c.

с – фокустары ара қашықтығының жартысы; 2а - тұрақты шама.
y


M(x, y)
b
r₁
r₂
x
a

F₁ А₂(-а;0) А₁(а;0) F₂
Мұндағы, .

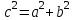- гиперболаның нақты жарты осі;

- гиперболаның жорамал жарты осі.

Фокустың координаталары және болады.

Анықтама: Қабырғалары тең және гиперболаның осьтеріне параллель болатын, центрі гиперболаның центрімен беттесетін тік төртбұрыштың негізгі диоганалдары гиперболаның асимптоталары деп аталады.

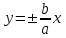теңдеуімен анықталатын түзуді гиперболаның асимптотасы дейміз.

Гиперболаның эксцентриситеті деп 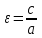қатынасын айтады.

a - гиперболаның центрінен оның төбесіне дейінгі қашықтық

Анықтама: Гиперболаның фокалдық осіне перпендикуляр және центрінен / a қашықтықтағы түзулер гипербола директрисалары деп аталады.

Директриса теңдеулері: х=a/ . x  a/ 

Кез-келген гипербола үшін .

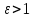3. 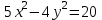гиперболаның теңдеуі берілген.

а) жарты осьтерінің ұзындығын;

ә) фокустарының координаттарын;

б) гиперболаның эксцентриситетін;

в) асимптотасының теңдеуін табу керек.

▼ Екі жағын 20-ға бөліп, гиперболаның канондық теңдеуіне келтіреміз:

---

.

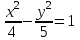а) 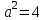, , 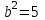яғни , .

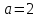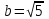ә) формуласы бойынша, 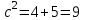, 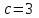. Бұдан , .

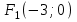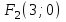б) Формула бойынша .

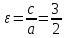в) гиперболаның асимптотасының формуласы бойынша .▲
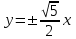Анықтама: Белгіленген нүктеге дейінгі және осы нүкте арқылы өтпейтін берілген түзуге дейінгі қашықтықтары тең болатын жазықтықтағы нүктелердің геометриялық орны парабола деп аталады.

Белгіленген нүкте параболаның фокусы, берілген түзу параболаның директрисасы деп аталады. Фокустан директрисаға дейінгі қашықтықты параболаның фокалдық параметрлері және р деп белгіленеді

4. Парабола дегеніміз – фокус деп аталатын 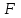нүктесінен директриса деп аталатын 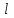түзуінен бірдей қашықтықта жататын нүктелердің жиыны.

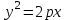(4)

формула параболаның канондық теңдеуі деп аталады.

Фокус координаталары ;

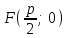Директриса теңдеуі
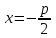
Параболаның симметрия осімен қиылысу нүктесін оның төбесі дейміз.

Кез-келген парабола үшін .
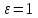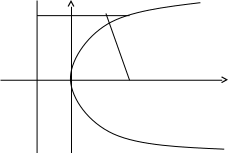у

А М(х, у)

О F x




p/2 p/2
р шама (фокустан директрисаға дейінгі қашықтық) параболаның параметрі деп аталады. Параболада асимптота болмайды.

---

Параболаның қасиеттері:

1. 
   (*) теңдеудегі у жұп дәрежелі болғандықтан, парабола Ох өсіне қарағанда симметриялы, Ох өсі параболаның симметрия өсі болады.
   

2. 
   р0 болғандықтан, (*) теңдеуден х0. Сондықтан, парабола Оу өсінің оң жағында орналасады.
   
3. 
   х  0 болғанда, у  0. Демек, парабола координат басы арқылы өтеді.
   
4. 
   х шектеусіз өскен сайын у-тің модулі де шектеусіз өседі. О(0; 0) нүкте параболаның төбесі , ҒМ  г М нүктесінің фокальдық радиусыболады.
   

4. 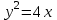парабола берілген.

а) фокусының координатасын;

ә) директрисасының теңдеуін табу керек.

▼

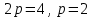
Фокус координатасы ;

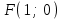Директриса теңдеуі формуласы бойынша ▲

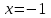Пайдаланған әдебиеттер:

1. 
   Айдос Е.Ж. Жоғары математика (қысқаша курс). Оқулық. Алматы.: «Иль-Тех-Кітап» ЖШС, 2003.
   
2. 
   Ефимов Н.В. Краткий курс аналитической геометрии / Н.В. Ефимов. –М.: Наука, 1969. -272 с.
   
3. 
   Әубәкір С.Б. Жоғары математика I,II-бөлім. – Алматы.: ҚазҰТУ, 2000
   
4. 
   Дүйсек А.К. Жоғары математика, / А.К. Дүйсек, С.К. Қасымбеков. –Алматы: 2004. – 439 с.
   

---

Смотрите также файлы

• Дисциплина Менеджмент Тема курсовой работы.docx

• Пояснительная записка к курсовой работе по дисциплине Машины и оборудование для бурения нефтяных и газовых скважин 210301. 090. 000 Пз.docx

• Таова Радмила Ибрагимовна Место работы мбоу Гимназия 4 г. УстьДжегуты общая информация по уроку класс укажите класс, к которому относится урок.docx

• 1умар Гайсултанов.pptx

• азастанны егемен мемлекет ретінде алыптасуы мен Даму стратегиясы.docx