ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 45
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
Расчетно-графическая работа
На тему «Исследование функции и построение её графика»
18 вариант
Выполнил: студент гр. ___НБ-22-1_____Занг Атангана Закари Фабрис_____
Проверил: ___доцент Бакеева Лариса Викторовна___
Санкт-Петербург 2023
Содержание
Содержание 2
Введение 3
Основная часть 4
Теоретическое описание 4
Практическая часть 5
Заключение 12
Список используемое литературы 13
Введение
Цели и задачи: В данной работе я проведу исследование функций, которое содержит в себе несколько этапов, построю графики функций, выявлю закономерности, с которыми столкнусь по ходу решения и продемонстрирую методы решения, которые были изучены в ходе подготовки к данной работе. За теоретическую основу будет взяты записи лекций и методические материалы, описанные в конце документа. Основной задачей данной работы является правильная интерпретация полученных по ходу решения данных для построения графика функции.
Методы решения: Определение области определения функции. Проверка функции на симметричность. Нахождение пересечения графика с осью координат. Вычисление асимптот к графику функций. Нахождение максимумов/минимумов и областей выпуклости функции (точек перегибов) с помощью производных первого и второго порядка соответственно. Построение графика функции для наглядного изучения.
Основная часть
Теоретическое описание
При решении данной расчетно-графической работы по теме «Применение производной при построении графика функции» мною были использованы следующие этапы:
-
Определение области определения функции D(y) -
Проверка функции на симметричность
-
Четность: y(-x)=y(x) -
Нечетность: y(-x)=-y(x) -
Несоблюдение первых двух условий приводит к выводу о несимметричности функции
Нули функции:
-
X=0 -
Y=0
Вычисление асимптот к графику или определение их отсутствия с помощью следующих пределов:
-
Вертикальные асимптоты: вывод об их отсутствие делается на основе изучения пункта 1: если D(y)R, то вертикальные асимптоты отсутствуют. В ином случае вычисляется предел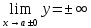 , в качестве а берутся значения всех граничных точек из области определения функции
, в качестве а берутся значения всех граничных точек из области определения функции -
Наклонные асимптоты: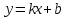
Частным случаем наклонной асимптоты является горизонтальная асимптота - критерий k=0, b=const
-
Нахождение максимумов/минимумов функции производится через вычисление первой производной и соотнесения на числовой оси полученных значений, на основе которых делается вывод об областях возрастания/убывания функции и точках экстремума -
Определение областей выпуклости функции и точек перегиба производится на основе вычисления вторых производных (аналогично пункту 4) -
Построение графика на основе полученных данных
Практическая часть
Задание 3. Исследовать функции и построить их графики
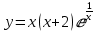 2)
2)
Ход решения:
-
Функция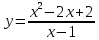
-
Область определения функции: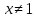 ; D(y)=(-∞;1)(1;+∞)
; D(y)=(-∞;1)(1;+∞) -
Проверка критерия четности/нечетности:
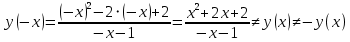
Делаем вывод, что функция является несимметричной (функция общего вида) непериодическая.
Нули функции:
OY: x=0;
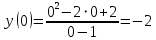 ; (0;-2)
; (0;-2)OX: y=0; y(x)=0;

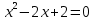
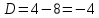 ; -4<0; значит график не имеет пересечений с осью OX.
; -4<0; значит график не имеет пересечений с осью OX.-
Асимптоты функции:
x=1 является точкой разрыва 2го рода, вертикальной асимптотой, т.к.
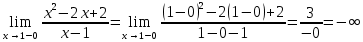
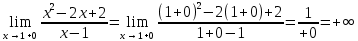
Ищем наклонную асимптоту:

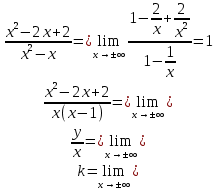
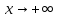 :
: 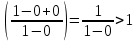
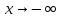 :
: 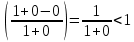
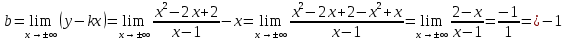
Следовательно, наклонной асимптотой является:
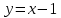
-
Области возрастания и убывания. Максимумы/минимумы функции
Рассмотрим первую производную функции и найдём её нули:
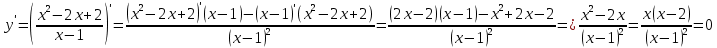
x=0 или x-2=0; x=2.



 y’ + 0 - 1 - 2 +
y’ + 0 - 1 - 2 +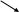
 y
yКак можно заметить из графического пояснения: область убывания функции (0;1)
(1;2), а область возрастания функции (-∞;0]
 [2;+ ∞). Из этого делаем вывод, что точкой локального минимума функции является точка:
[2;+ ∞). Из этого делаем вывод, что точкой локального минимума функции является точка:Min y(x): y(2) =
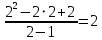 .
.Точка локального максимума:
Max y(0) =
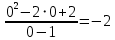 .
. -
Области выпуклости, вогнутости; точки перегиба:
Рассмотрим вторую производную функции и найдём её нули:
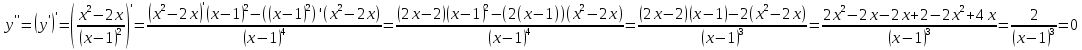


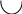 y’’ - 1 +
y’’ - 1 + y
yТак как
 по ООФ, то точки перегиба нет.
по ООФ, то точки перегиба нет.Из графического описания видно, что функция выпукла вверх на промежутке (-∞;1) и выпукла вниз (вогнута) на промежутке (1;+ ∞)
-
Построение графика на основе полученных данных:
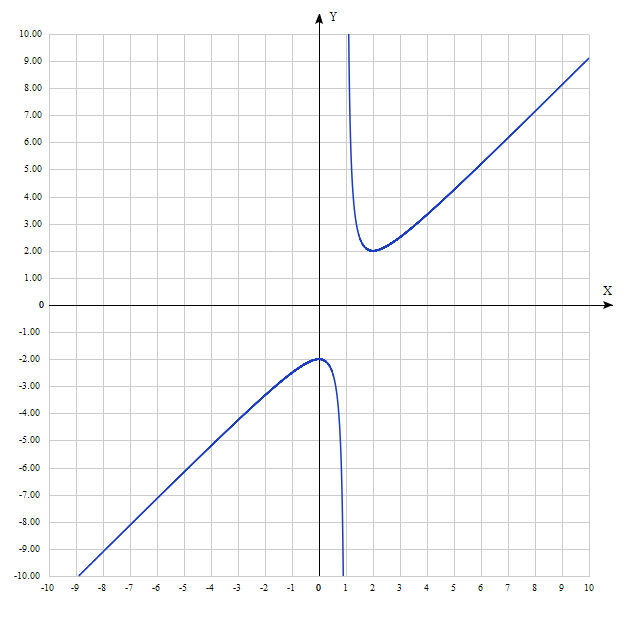
Рис.1. График функции

-
Функция
-
Область определения функции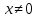 ; D(y)=(-∞;0)(0;+∞)
; D(y)=(-∞;0)(0;+∞) -
Проверка критерия четности/нечетности:
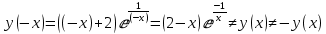
Делаем вывод, что функция является несимметричной (функция общего вида) непериодическая.
Нули функции:
OY: Так как по ООФ
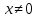 , то график не имеет пересечений с осью OY.
, то график не имеет пересечений с осью OY.OX: y=0; y(x)=0;
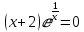
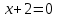 ;
; 
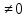
x = -2. Значит с осью ОХ график пересекается в точке (-2;0)
-
Асимптоты функции:
x=0 является точкой разрыва 2го рода, вертикальной асимптотой, т.к.
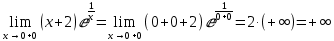
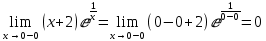
Так как хотя бы один из односторонних пределов равен
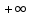 , то x=0 является вертикальной асимптотой.
, то x=0 является вертикальной асимптотой.Ищем наклонную асимптоту:

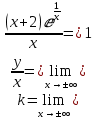
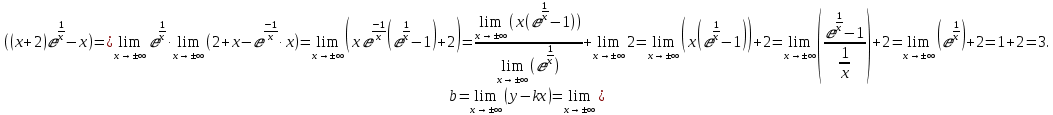
Следовательно, наклонной асимптотой является:
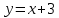
-
Области возрастания и убывания. Максимумы/минимумы функции
Рассмотрим первую производную функции и найдём её нули:
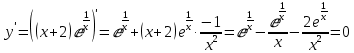
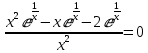
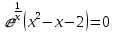
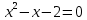
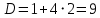
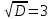

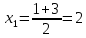
y’ + -1 - 0 - 2 +



 y
yКак можно заметить из графического пояснения: область убывания функции [-1;0)
 (0;2], а область возрастания функции (-∞;-1]
(0;2], а область возрастания функции (-∞;-1]  [2;+ ∞). Из этого делаем вывод, что точкой локального минимума функции является точка:
[2;+ ∞). Из этого делаем вывод, что точкой локального минимума функции является точка: