Файл: Исследование функции и построение её графика.docx

Min y(x): y(2) = .

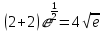Точка локального максимума:

Max y(-1) = ..

5. 
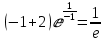   Области выпуклости, вогнутости; точки перегиба:
   

Рассмотрим вторую производную функции и найдём её нули:



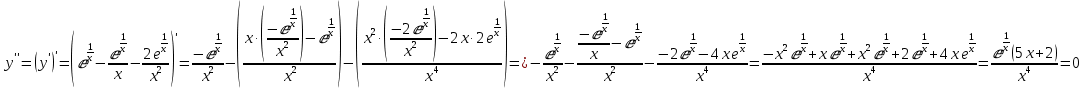
5x+2=0

x= - 0,4

y’’: - -0,4 + 0 +




y

Из графического описания видно, что функция выпукла вверх на промежутке (-∞;-0,4] и выпукла вниз (вогнута) на промежутке [-0,4;0) (0;+∞).

Найдём точку перегиба: y(-0,4) =

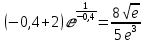
Координаты точки перегиба: (-0,4; )

6. 
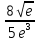   Построение графика на основе полученных данных:
   

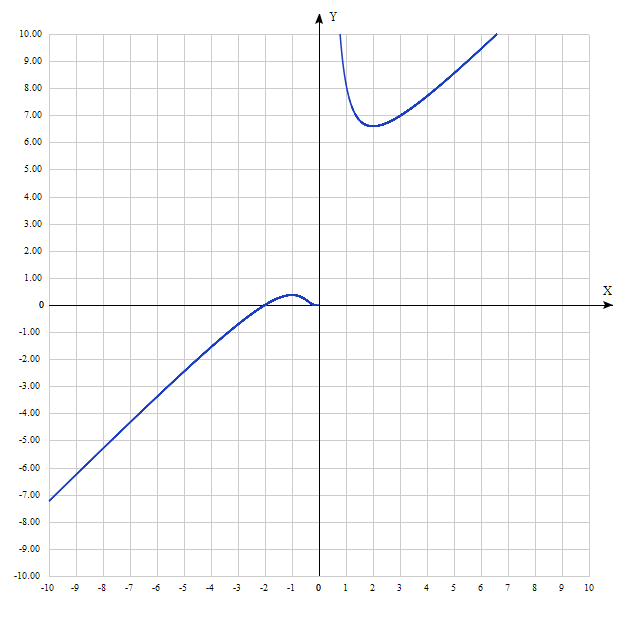
Рис. 2. График функции
Задание 4. В прямоугольный треугольник с гипотенузой 16 см и углом 60 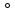вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть размеры прямо-угольника, чтобы его площадь была наибольшей?










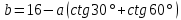
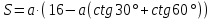
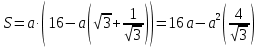
Для нахождения максимальной площади прямоугольника, найдём первую производную площади выраженной через a и найдем максимальное значение а приравняв производную к нулю:







;

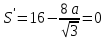
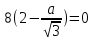
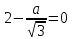
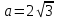Подставим полученное значение в формулу нахождения b:



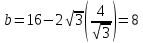
Таким образом исходные размеры прямоугольника: ; .

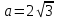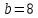Ответ: ; .

---

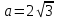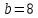Заключение

По итогу проведённой работы были на практике использованы основные методы исследования функций и построены графики (Задача 3), а также решена практическая задача с использованием метода производной для нахождения экстремума функции (Задача 4).

Основные теоретические этапы, использованные для проведения работы:

1. 
   Определение области определения функции D(y)
   
2. 
   Проверка функции на симметричность, Нули функции.
   
3. 
   Вычисление асимптот к графику
   
4. 
   Нахождение областей возрастания и убывания функции, максимумов и минимумов.
   
5. 
   Определение областей выпуклости (вогнутости) функции и точек перегиба.
   
6. 
   Построение графиков
   

В результате выполнения работы были освоены основные постулаты построения графиков путём математического анализа, а также полученные знания были применены на практике при решении задачи 4.

Список используемое литературы

1.Высшая математика Том2 Начало математического анализа. Дифференциальное исчисление функций одной переменной и его приложения .Электрон. текстовые данные. – СПб.: Санкт-Петербургский горный университет, 2015.–104c.
2.Данко П.Е. Высшая математика в упражнениях и задачах. Учебное пособие для студентов ВУЗов / Данко П.Е., Попов А.Г., Кожевников Т..Я. – М.: АСТ, 2014. 3.Дифференциальное и интегральное исчисления / Пискунов Н.С.. – СПб.: Ленанд, т.т.1-2, 2017.

---