ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 39
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Домашнее задание №1. Методы одномерного поиска
Цель работы: Ознакомиться с методами одномерного поиска. Выполнить задания.
Задание: Дана функция. Найти минимум функции min f(x),
-
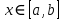
Классическая минимизация функции одной переменной
Функция
-
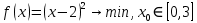
Находим производную функции
-
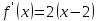
Находим корни уравнения
-
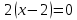
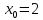
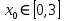
Находим значение функции f(x0)
-
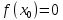
Находим минимум
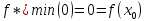
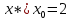
Ответ:
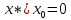
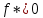
Функция
-
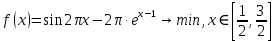
Находим производную функции
-
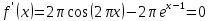
Находим корни уравнения
-
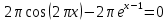
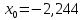
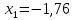
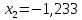
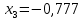
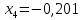
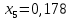
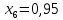
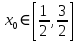
Находим значение функции f(x0)
-
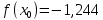
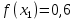
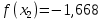
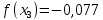
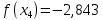
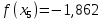
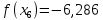
Находим минимум
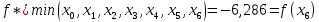
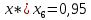
Ответ:
-
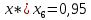
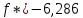
Метод деления отрезка пополам с точностью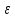
=0,1. -
Функция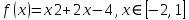
| a | -2 |
| b | 1 |
| e | 0,1 |
Условия на сходимость
| f(a) | -4 | точность |
| f(b) | 8 | ✅ |
Действие по методу
| a | -2 | -2 | -1,25 | -1,25 | -1,0625 | -1,0625 |
| b | 1 | -0,5 | -0,5 | -0,875 | -0,875 | -0,96875 |
| x | -0,5 | -1,25 | -0,875 | -1,0625 | -0,96875 | -1,015625 |
| f(a) | -4 | -4 | -1 | -1 | -0,25 | -0,25 |
| f(x) | 2 | -1 | 0,5 | -0,25 | 0,125 | -0,0625 |
| условие точности | ❌ | ❌ | ❌ | ❌ | ❌ | ✅ |
Ответ:
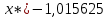
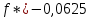
Домашнее задание №2. Методы одномерной оптимизации без
использования информации о производной функции
Цель работы: Ознакомиться со следующими методами оптимизации: золотого сечения,Фибоначчи, методами аппроксимации.
Задание 1: Найти аналитическое решение задачи min f(x),
различной точностью (
1=0,1; 2=0,001).1.1. Метод золотого сечения
Функция
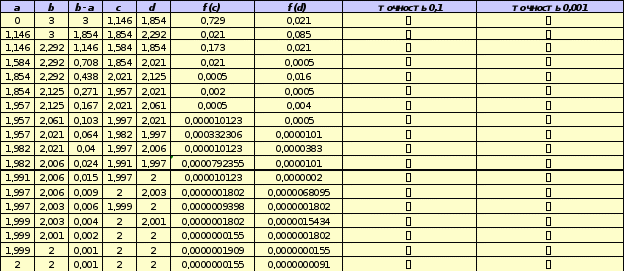
Ответ: При
1=0,1;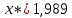 
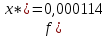
При
1=0,001;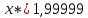 
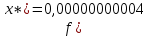
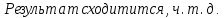
1.2. Метод Фибоначчи
Функция
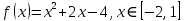
| a | -2 |
| b | 1 |
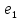 | 0,1 |
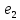 | 0,01 |
Фибоначчи
| n | Fn |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 5 |
| 6 | 8 |
| 7 | 13 |
| 8 | 21 |
| 9 | 34 |
| 10 | 55 |
| 11 | 89 |
| 12 | 144 |
| 13 | 233 |
| 14 | 377 |
| 15 | 610 |
| 16 | 987 |
Проверка номера иттерации и последнего члена последовательности
Для
1=0,1;| N | /0 | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | последний |
Для
2=0,001;| N | /0 | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | ❌ | последний |
Действия по методу
Для
1=0,1;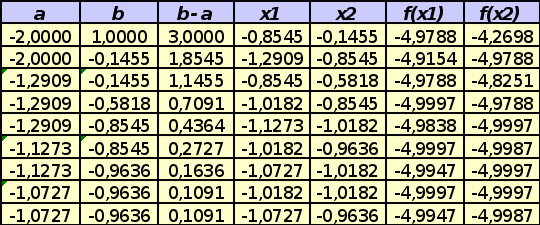
Ответ: Для
1=0,1; n=9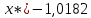
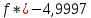
Для
2=0,001;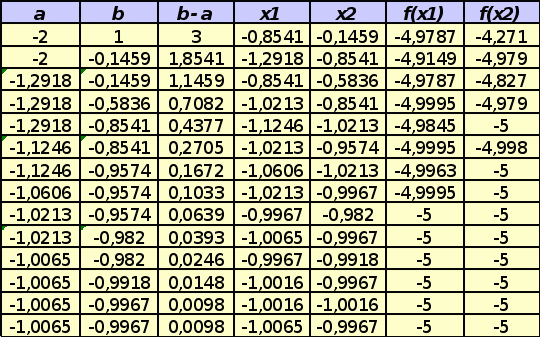
Ответ: Для
2=0,001; n=14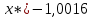
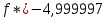
Функции из домашнего задания 1 разные.
1.3. Метод квадратичной аппроксимации (или метод Пауэлла)
Функция
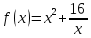
На отрезке [1,4]
Решим уравнение:
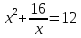
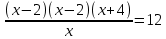
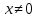
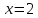
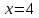
| h | 1 |
 | 0,1 |
 | 0,01 |
Действия по методу:
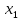 | 1 |
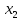 | 2 |
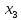 | 3 |
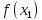 | 17 |
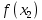 | 12 |
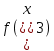 | 14,3 |
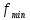 | 12 |
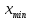 | 2 |
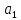 | -5 |
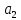 | 3,667 |
| x* | 2,182 |
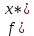 | 12,094 |
| окончание итерации | ✅ |
Ответ:
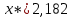
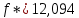
Действия по методу: