1	1	1	1
	2	2	2	2
	3	2,182	2,036	2,007
	17	17	17	17
	12	12	12	12
	14,3	12,094	12,004	12,0002
	12	12	12	12
	2	2	2	2
	-5	-5	-5	-5
	3,667	4,667	4,930	4,99
x*	2,182	2,036	2,007	2,001
	12,094	12,004	12,0002	12,000006
окончание итерации	❌	❌	❌	✅

---

Ответ:




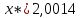
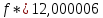
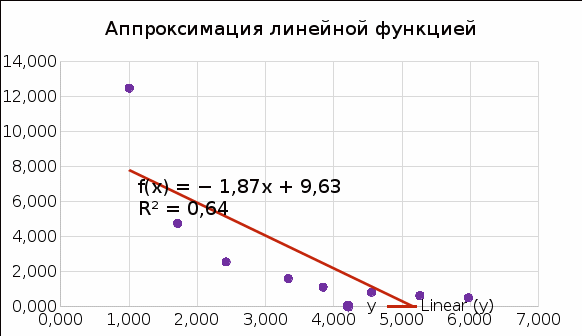
Цель работы: Ознакомиться с аппроксимацией методом наименьших квадратов.

Задание 1: Найти приближающую функцию к данной на основании критерия наименьшей суммы квадратов. Рассмотреть несколько видов аппроксимирующих видов функций.

Даны значения функции, представленные в таблице:

X	1	1,71	2,42	3,33	3,84	4,55	5,26	5,97
Y	12,49	4,76	2,55	1,60	1,11	0,82	0,63	0,50

Функция

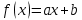
Действия по методу:



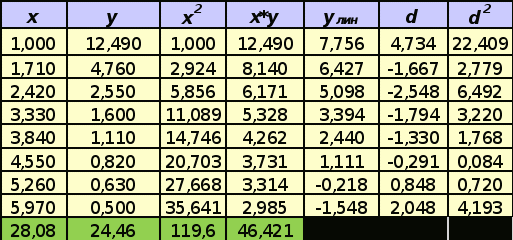
Находим коэффициенты:

S 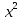=119,6

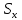=28,08

N=8
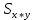=46,42

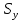=24,46
a=-1,87

b=9,63

Приближающаяся функция: y = -1,87x + 9,63



Функция

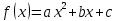
Действия по методу:



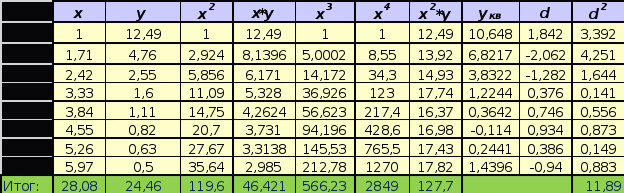
Находим коэффициенты:

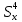=2849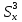

=566,2

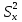=119,6

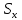=28,0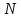8

=8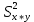
=127,7

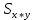=46,42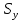

---

=24,46
a=0,83

b=-7,64

c=17,46

Приближающаяся функция: y = 0,83x² - 7,64x + 17,46



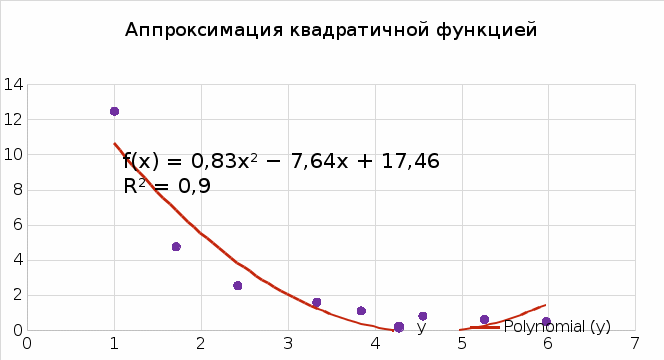
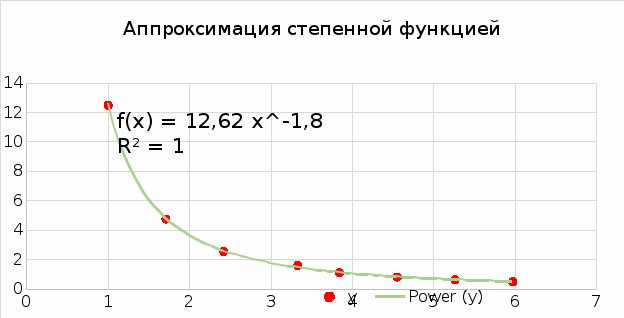
Функция

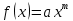
Приближающаяся функция: y =12,62x^-1,8


Функция

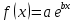
Приближающаяся функция: y = 14,67e^-0,61x


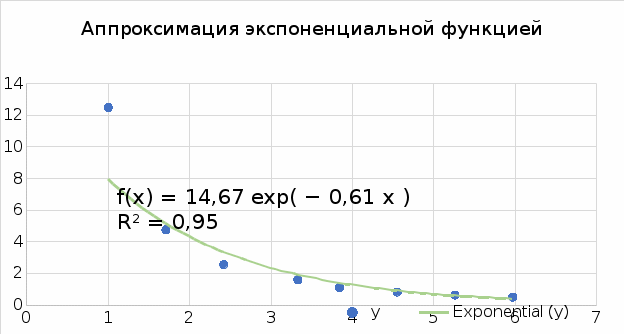
Функция

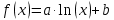
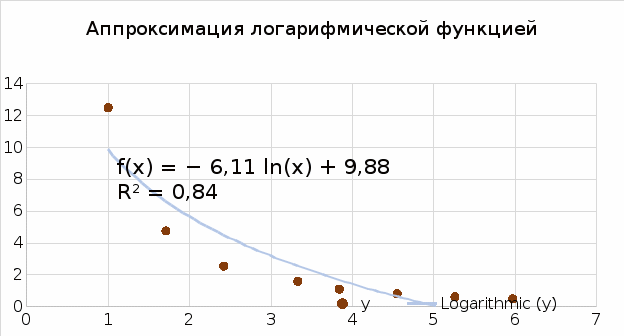
Приближающаяся функция: y = -6,1∙ln(x) + 9,88


Функция

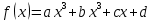
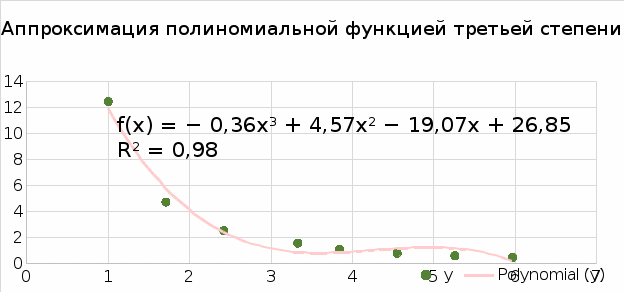
Приближающаяся функция: y = -0,36x³ + 4,57x² - 19,07x + 26,85



Вывод: при выполнении данной работы мною были изучены методы одномерного поиска, а именно метод классической минимизацией, метод деления отрезка пополам, метод золотого сечения, метод Фибоначчи, метод Пауэлла и аппроксимация методом наименьших квадратов.

---

Смотрите также файлы

• Срок прохождения практики с 15 мая 2023 г по 29 мая 2023 г.docx

• "Газовая реле".pptx

• Теоретические основы формирования, назначение бухгалтерского баланса и анализ финансового состояния.docx

• Реферат по дисциплине экспертиза и оценка качество товаров.docx

• Исследование функции и построение её графика.docx