Файл: Задача Параллельные прямые а и b лежат в плоскости.docx
Добавлен: 23.11.2023
Просмотров: 89
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задачи на тему «параллельность прямых и плоскостей»
Задача 1.
Параллельные прямые а и b лежат в плоскости .
Докажите, что прямая с, пересекающая прямые а и b, также лежит в плоскости а.
Дано: а || b, а ∈ а, b ∈ а, с ∩ а=А, с ∩ b=B.
Доказать: с ∈ а.
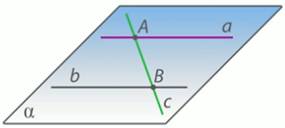
Доказательство:
Точка А прямой с, принадлежит и прямой а, а значит, и плоскости а. Точка В прямой с принадлежит прямой b, а значит, и плоскости а. Так как две точки прямой с принадлежат плоскости а , то и вся прямая лежит в плоскости а , в силу аксиомы А2.
Задача 2.
Стороны AB и BC параллелограмма ABCD ∩ а. Докажите, что прямые AD и DC также ∩ а.
Дано: ABCD – параллелограмм, AB ∩ а=М, ВС ∩ а=N
Доказать, что прямые AD и DC ∩ а.
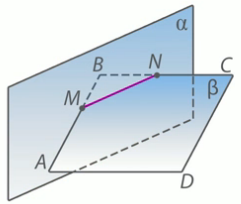
Обозначим плоскость АВС как B. . Тогда плоскости a и B ∩ MN.
Прямая АВ ∩ a, и прямые АВ ||CD ( как стороны параллелограмма). Тогда, согласно лемме, прямая CD ∩ а. Аналогично, прямая ВC ∩ а, и прямые ВС II АD (как стороны параллелограмма). Тогда, согласно лемме, прямая АD ∩ а, что и требовалось доказать.
Давайте найдем эти точки пересечения. Пусть прямая CD ∩ а в точке Q, а прямая АD ∩ а в точке F.
Плоскости а и B ∩ MN, значит, все их общие точки лежат на этой прямой. Продолжим прямые CD и АD до их пересечения с прямой MN и получим соответственно точки Q и F.
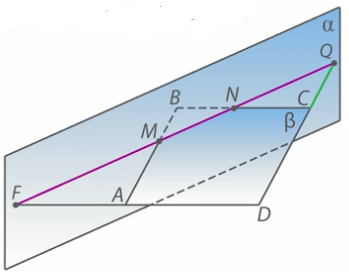
Задача 3.
Средняя линия трапеции лежит в плоскости а, не совпадающей с плоскостью B. . Пересекаются ли прямые, содержащие основания трапеции, с плоскостью а?
Дано: ABCD – трапеция, MN – средняя линия.MN ∈ a, a не равно B.
Найти: пересекают ли прямые AD и ВC плоскость а?
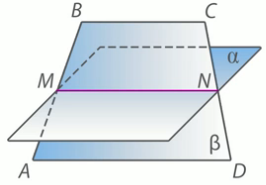
Решение:
Вспомним, что средняя линия трапеции параллельна ее основанием. Значит, прямые AD II MN, а прямая MN ∈ а. Значит, по признаку параллельности прямой и плоскости, AD II а.
Задача 4.
Точка D не лежит в плоскости прямоугольника KLMN. Доказать, что MN || DKL.
Дано: KLMN – прямоугольник,D не принадлежит KLM.
Доказать: MN || DKL
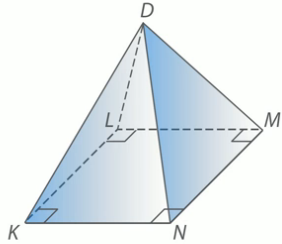
Доказательство:
Прямые KL || MN, а прямая KL ∈ DKL. Следовательно, по признаку параллельности прямой и плоскости, MN || DKL, что и требовалось доказать.
Домашнее задание:
-
Верно ли утверждение: если 2 прямые не имеют общих точек, то они параллельны? -
Параллельные прямые АС И ВD пересекают плоскость а в точках А И В. Точки С и D лежат по одну сторону от плоскости а, АС=8см,BD=6 см, АВ=4 см.
А) Докажите, что прямая CD пересекает плоскость а в некоторой точке Е.
Б) Найдите отрезок ВЕ.
-
На сторонах АВ и АС треугольника АВС взяты точки D и E так, что ОE = 5 см и ВD = 2/3. Плоскость a проходит через точки B и С, и параллельна отрезку ОE. Найдите длину отрезка ВС. -
Через каждую точку из двух параллельных прямых а и b и точку М, не лежащую в плоскости этих прямых, проведена плоскость.
Докажите, что эти плоскости пересекаются по прямой, параллельной прямым a и b.