ТЕМА – НАРАЩИВАНИЕ ПО СЛОЖНОЙ ПРОЦЕНТНОЙ СТАВКЕВ средне- и долгосрочных операциях, если процент не выплачивается сразу после их начисления, а присоединяется к сумме долга для наращивания, как правило, применяются сложные проценты:S = P × (1+ i )ⁿ, (1)где S – наращенная сумма по схеме начисления сложных процентов, р.;P – исходная сумма, р.;n – количество выплат, раз;i – ставка наращения, в долях единицы.База для начисления сложных процентов не остается постоянной – она увеличивается во времени с каждым шагом, т.е. проценты начисляются на ранее начисленные проценты. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, часто называют капитализацией процентов. Величину (1+i)ⁿ называют множителем наращивания по сложным процентам (Обозначим ее буквой q). Этот множитель показывает, чему будет равна одна денежная единица через n периодов при заданной процентной ставе i. Текущая стоимость денег находится с помощью коэффициента дисконтирования, исходя из формулы 1:Р = S × , (2)где - коэффициент дисконтирования.Текущая стоимость денег показывает, какую сумму необходимо вложить сегодня, чтобы получить определенный доход в будущем по действующим ставкам. Начисление процентов по переменным ставкамФормула S = Р × (1+ i )ⁿ предполагает постоянную ставку на протяжении всего срока начисления процентов. Неустойчивость кредитно-денежного рынка, а также при заключении долгосрочных кредитных договоров заставляют применять плавающие ставки. Исходя из этого, формула сложного процента преобразуется в следующую: S = Р × ( 1+ i₁ )ⁿ₁× ( 1+ i₂ )ⁿ₂ × … × ( 1+ i_k )ⁿ_k, (3)где S – наращивание процентов по переменной (плавающей) ставке, р.; Р – первоначально вложенный капитал, р.;

---

i₁, i₂, … i_k – последовательные во времени значения ставок, %;

n₁, n₂, … n_k – периоды, в течение которых работают соответствующие ставки, лет.

Наращивание процентов при неравном сроке вкладов и депозитов
Часто срок начисления процентов не является целым числом (при условии, что он больше года). При учете общего срока применяют два метода:

- расчет ведется по формуле сложного процента (8), при наличии технического калькулятора;

- смешанный метод, предполагает начисление процентов за целое число лет по формуле сложного процента (8), за дробную часть периода – по формуле простого процента (3). При этом формула будет иметь следующий вид:

S = Р ×(1+ i )^а × ( 1+ b × i ), a + b = n, (4)
где S – наращивание процентов при неравном сроке, более одного года, р.;

Р – первоначально вложенный капитал, р.;

a – целое число периодов, лет;

b – дробная часть периода (находится как 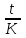, где t – срок кредита, дн.

К – временная база, равная количеству дней в календарном году;

i – ставка наращения, в долях единицы.
Решить задачи

1. 
   Какой величины достигнет долг, равный 1 млн. р. через 5 лет при росте по сложной ставке 15,5 % годовых.
   

Решение: Определить величину, до которой достигнет долг, по формуле: S = P (1+i), где S - наращенная сумма i - процентная ставка P - сумма капитала n - период величины долга S = 1 000 000 * (1 + 0,155)= 2055464, 22 руб. Ответ: 2055464, 22 руб.2. Рассчитать наращенную сумму с исходной суммы 1 млн. р. при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 20%; б) период наращения – 180 дн., 1 год, 5 лет, 10 лет. Расчеты представить в таблице 5.Таблица 5 – Наращивание по простой и сложной процентной ставке

Схема начисления	180 дн. n =	1 год n =	5 лет n =	10 лет n =
Простые проценты
Сложные проценты

---

Решение:i – 20% - 0,20t - 90t -180t – 1г.n -5л.P -1000S = P (1+i*t/360)S = P*(1+i)ⁿS = 1000*(1+0,20*90/360)=1050S =1000*(1+0,20*180/360)=1010S =1000*(1+0,20) = 1200S =1000*(1+5*0,20)= 2000S = P* (1 + i)* tS = 1000* (1+0,20) 90/360=300S =1000*(1+0,20)180/360=600S =1000*(1+0,20)*1=1200S =1000*(1+0,20)*5= 6000Ответ: наращенная сумма за периоды составила: 90дн.=300т.р.; 180дн.=600; 1год=1200т.р.; 5лет=6000т.р.

3. 
   Акционерное общество разместило капитал на депозитных счетах в двух банках А и Б по 100000 р. каждый. Срок действия депозитов - 2 года. Ставка – 36 % годовых. В банке А выплаты производятся поквартально, в банке Б – ежемесячно. Найти суммы вклада в банках А и Б. Сделать вывод по задаче.
   

Решение: Фрмула сложных процентов имеет вид: A = P × (1+ r) nt A - итоговая сумма. P - начальная сумма r - годовая процентная ставка n - количество периодов начисления процентов в год (напр. при ежемесячном начислении процентов количество таких периодов будет 12) t - срок инвестиций в годах. А = 100 000 * (1+0,36/12) ⁸ = 126 600 руб. Б = 100 000 * (1+0,36/12) ²⁴ = 203 000 руб. Таким образом, выгоднее размещать капитал с ежемесячным начислением процентов

3. 
   Акционерное общество приглашено для участия в инвестиционном проекте сроком на 2 года, по истечении, которого оно получит 100 тыс. р. Доходность данного проекта – 36 % годовых с ежеквартальными выплатами. Определить первоначальную сумму взноса.
   

Решение: Получит 100 тыс. ВСЕГО, т. е это вся сумма "на руки" суммарно после проекта (включая первоначальный возврат) х*1,36*1,36= 184,96 тыс. руб.х=184,36-100=84,36 тыс. руб.Получит 100 т. руб. именно ПО ИСТЕЧЕНИИ - то это самая последняя выплата (в конце последнего квартала) х* (1+0,36/4) =109 тыс. руб. х=109 тыс. руб. либо самый последний доход х*0,36/4=109 тыс. руб.

3. 
   Акционерное общество разместило капитал на депозитных счетах в трех банках: А, Б и С по 500 тыс. р. сроком на 3 года под 22 % годовых. При этом в банке А проценты начисляются ежеквартально, в банке Б – ежемесячно, а в С – по полугодиям. Определить, какая конечная сумма будет на счетах, и в какой банк выгоднее вложить капитал.
   

Решение: Фрмула сложных процентов имеет вид: A = P × (1+ r) nt A - итоговая сумма. P - начальная сумма r - годовая процентная ставка n - количество периодов начисления процентов в год (напр. при ежемесячном начислении процентов количество таких периодов будет 12) t - срок инвестиций в годах. 

---

А = 500 000 * (1+0,22/12) ¹²= 620 000 руб. Б = 500 000 * (1+0,22/12) ³⁶ = 960 000 руб. С = 500 000 * (1+0,22/12) ⁶ = 557 000 руб. Таким образом, выгоднее размещать капитал с ежемесячным начислением процентов

3. 
   Первоначально вложенная сумма равна 200 тыс. р. Определить наращенную сумму через 5 лет при использовании простых и сложных ставок процента в размере 28 % годовых. Решить этот пример для случая, когда проценты начисляются по полугодиям и по кварталам (сложная процентная ставка).
   

Решение:

1. 
   Наращенная сумма через 5 лет при использовании простой ставки процентов:
   

S = P * (1 + n*i) = 200 000 * (1 + 5*0,28) = 480 000 (руб.)

2. 
   Наращенная сумма через 5 лет при использовании сложной ставки процентов:
   

S = P * (1 + i)n = 200 000 * (1+0,28)⁵ = 687 194,7 (руб.)

3. 
   Наращенная сумма через 5 лет при начислении по полугодиям:
   

S = P * (1 + j/m)^mn = 200 000 * (1+0,28/2)2*5 = 741 444,3 (руб.) Ответ: выгоднее начислять проценты при использовании сложной ставки процентов.

3. 
   Срок вклада - 5 лет, договорная процентная ставка в первые два года – 12,5 %, в оставшиеся - 12,75 %. Сумма первоначального вклада - 100 тыс. р. Определить множитель наращивания и сумму вклада в конце срока.
   

Решение: Определим множитель наращивания = (1+(0.12.5*2+0.1275*3) = 1.6325 Рассчитаем сумму вклада в конце срока: S = 100 000 * 1,6325 = 163 250 руб.

3. 
   Капитал размещен в инвестиционном проекте на срок 3 года и 160 дней под 80 % годовых. Первоначальная сумма вклада - 300 тыс. р. Определить сумму капитала в конце срока.
   

Решение: Рассчитаем сумму капитала в конце периода: S = 300 000 * (1+(0,8*3+0,8/365*160) = 300 000 * 3,7506 = 1 125 180 руб.

---

Смотрите также файлы

• Административноправовые отношения.rtf

• Губарева Наталия Владимировна г. Москва 2023 Индивидуальное практическое занятие.rtf

• Домашние животные.docx

• Пао Сбербанк на примере кредитных карт.pdf

• Г. Т. Хоментаускас считает нужным анализировать рисунок семьи по трем уровням.docx