Файл: Учебное пособие Введение.doc

2.3.1. Характеристика однозначности для бинарных связей

1. 
   Связь 1:1, «один-к-одному». Эта связь означает, что каждому объекту из первого класса соответствует ровно один объект из второго класса и, наоборот, каждому объекту из второго класса соответствует ровно один объект из первого класса. В отношение вступают два объекта из разных классов.
   

Например, связь между классами Факультет и Декан. Факультет может иметь только одного декана, а декан может быть деканом только одного факультета. На схеме такая связь изображается двумя одинарными стрелками.

2. 
   Связь 1:M, «один-ко-многим» (или M:1, «многие-к-одному»). Эта связь означает, что одному объекту из первого класса соответствует несколько объектов второго класса, но каждому объекту второго класса соответствует только один объект первого класса. В такое отношение вступают несколько объектов – один объект из первого класса, остальные из второго, и если какой-то объект из второго класса уже входит в отношение с каким-то объектом из первого класса, то он уже не может входить в такое же отношение с другим объектом первого класса.
   

Такой характер носит связь между классами Группа и Студент. В группе может быть несколько студентов, но каждый студент может быть только в одной группе. Или отношение между классами Факультет и Кафедра. Факультет может иметь несколько кафедр, но каждая кафедра принадлежит только одному факультету.

На схеме связь изображается одной одинарной и одной двойной стрелками. Двойная стрелка направлена к тому классу, объекты которого могут входить в отношение в любом количестве.

3. 
   Связь M:N, «многие-ко-многим». Эта связь означает, что одному объекту первого класса соответствует несколько объектов второго класса и каждому объекту второго класса соответствует несколько объектов первого класса. В отношение входит несколько объектов от одного и от другого класса.
   

Например, связь между классами Преподаватель и Предмет. Преподаватель может читать несколько предметов, и каждый предмет могут читать несколько преподавателей.

На схеме такая связь изображается двумя двойными стрелками.

2.3.2. Характеристика полноты связи

Характеристика полноты отражает зависимость класса от связи, в которую он входит.

---

1. 
   Необязательная по отношению к классу связь означает, что существование объектов класса не зависит от наличия связи.
   
2. 
   Обязательная по отношению к классу связь означает, что существование объектов класса зависит от наличия связи.
   

На схеме обязательная по отношению к классу связь обозначается квадратом с точкой внутри, примыкающим к прямоугольнику, представляющему класс, перед входящей в него стрелкой связи.
Например:

1. 
   Связь между классами Факультет и Компьютерный класс. В университете есть факультеты, не имеющие компьютерных классов, и есть компьютерные классы, не приписанные ни к одному из факультетов, т. е. и компьютерные классы, и фа­куль­те­ты существуют вне зависимости от того, относится ли компьютер­ный класс к факультету и имеет ли факультет хотя бы один компьютерный класс. Такая связь является необязательной и по отношению к классу Факультет, и по отношению к классу Компьютерный класс.
   

2. 
   Связь между классами Служащий и Должность. Каждый со­трудник в организации должен иметь какую-либо должность, т. е. нет сотрудника без должности. Это означает, что не существует объекта класса Служащий, не связанного с каким-либо объектом класса Должность. Но должность может быть и вакантной, т. е. быть не связанной ни с одним объектом класса Служащий. Такая связь является обязательной по отношению к классу Служащий и необязательной по отношению к классу Должность.
   

3. 
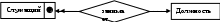
   Связь между классами Студент и Группа. Не может быть студента, не принадлежащего ни к одной группе, так же как не может быть группы без студентов. Такая связь является обязательной и по отношению к классу Студент, и по отношению к классу Группа.
   

Общая схема, содержащая все классы объектов, их свойства, связи между классами и свойства этих связей, и будет инфологической моделью предметной области, иногда ее называют концептуальной моделью.

После того как построена инфологическая модель предметной области, можно переходить к построению модели данных.

---

---

3. Реляционная модель данных

Модель данных является моделью логического уровня и представляет собой отображение логических связей между элементами данных безотносительно к их содержанию. Эта модель строится в терминах информационных единиц, допустимых в конкретной системе управления базами данных, в среде которой мы проектируем базу данных.

Модель данных включает в себя структуру данных, множество операций над данными и ограничения целостности. Можно назвать четыре основных модели данных: сетевая, иерархическая, реляционная и объектная. В основе их классификации лежит структура данных.

Рассмотрим наиболее популярную модель данных – реляционную, основанную на некоторых положениях математики (в основном теории множеств и логике предикатов). Название модели произошло от английского слова «relation», что в переводе означает отношение, именно математическое отношение лежит в основе структуры реляционной модели. Принципы реляционной модели были заложены в 1969–70-х годах американским ученым Е. Ф. Коддом (E. F. Codd), в то время работавшим в корпорации IBM. За эту модель Кодд был удостоен престижной премии Тьюринга в области теоретических основ вычислительной техники.

3.1. Структура

Начнем описание структуры реляционной модели данных с нескольких определений.

Доменом называется множество однородных элементов. Домены являются произвольными непустыми конечными или счетными множествами. Например, множество названий дней недели, множество целых чисел, состоящих не более чем из 10 цифр, множество символьных строк длиной 20 символов и т. п.

Атрибутом называется именованный домен, представляющий свойство объекта или связи. Разные атрибуты могут иметь одинаковые домены.

Например:

Атрибут	Домен
Фамилия	строка символов длиной не более 30 символов
Название города	строка символов длиной не более 25 символов
Номер квартиры	натуральное число
Кол-во ед. товара	натуральное число
Стипендия	вещественное число с двумя знаками после запятой
Форма детали	круг, квадрат, шестиугольник

---

Схемой отношения R называется конечное множество имен атрибутов (A₁,A₂,…, A_n). Каждому атрибуту с именем A_i соответствует домен D_i, i=1,…,n. Введем обозначение: dom(A_i) = D_i. Количество атрибутов (n) называется степенью отношения.

Пусть D = D₁  D₂  …  D_n – декартово произведение всех доменов схемы отношения.
Отношением r со схемой R называется конечное подмножество в D:

r(R)={t₁,t₂,…,t_p},

где p – количество элементов, входящих в отношение r(R). Каждый элемент отношения (t) называется кортежем. Кортеж состоит из данных (t(A_i)) значений кортежа t на атрибуте A_i. Каждое данное должно принадлежать домену соответствующего ему атрибута, т. е. удовлетворять следующему ограничению: t(A_i)  D_i, i=1,…,n.

Определим схему отношения Студент с атрибутами Фамилия, Год_рождения, Год_поступления, Номер_билета, Курс_обучения, Стипендия:

Студент(Фамилия, Год_рождения, Год_поступления, Номер_билета, Курс_обучения, Стипендия).

В качестве доменов для атрибутов отношения Студент могут выступать следующие множества:

dom(Фамилия) = {строка символов длиной 20};

dom(Год_рождения) = dom(Год_поступления) = {множество четырехзначных натуральных чисел};

dom(Номер_билета) = {множество шестизначных натуральных чисел};

dom(Курс_обучения) = {1, 2, 3, 4, 5, 6};

dom(Стипендия) = {вещественное число с двумя знаками после запятой}.

Кортежами, удовлетворяющими схеме, могут быть:

t₁ = <Петров, 1978, 1994, 123456, 5, 100.50>,

t₂ = <Иванов, 1979, 1995, 122453, 4, 0.00>.

Тогда данными будут:

t₁(Год_рождения) = 1978,

t₂(Стипендия) = 0.00.

Отношение удобно представлять в виде таблицы.

Студент

Фамилия	Год_рож-дения	Год_посту-пления	Номер_би-лета	Курс_обу-чения	Стипендия
Петров	1978	1994	123456	5	100.50
Иванов	1979	1995	122453	4	0.00
Соколов	1975	1995	122454	4	90.00

---