Файл: Лабораторная работа 1 Определение момента инерции маховика Лабораторная работа разработана преподавателями кафедры.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 254
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Саратовский государственный технический университет
имени Гагарина Ю.А.
Энгельсский технологический институт

ЛАБОРАТОРНАЯ РАБОТА № 1
«Определение момента инерции маховика»
Лабораторная работа разработана преподавателями кафедры
«Естественные и математические науки» ЭТИ СГТУ им. Гагарина Ю.А.
Энгельс, 2023
Цель работы: изучение вращательного движения твердых тел, определение момента инерции маховика.
Основные понятия
Вращательное движение твердых тел
Вращательным движением тела называется такое движение, при котором траекториями всех точек тела являются концентрические окружности с центрами на одной прямой, называемой осью вращения.
Быстрота вращения характеризуется угловой скоростью или циклической частотой и обозначается
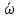 . Она равна изменению угловой координаты
. Она равна изменению угловой координаты 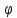 на единицу времени
на единицу времени 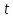 :
: 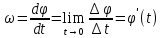 | (1) |
Единицей угловой скорости является 1 рад/с. Быстрота изменения угловой скорости характеризуется угловым ускорением
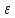 :
: 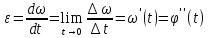 | (2) | |
 Рис. 1 | Скорость и ускорение – векторные величины. Вектор 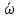 направлен по оси вращения. Его направление определяется правилом правой руки. Согните четыре пальца правой руки по направлению вращения. направлен по оси вращения. Его направление определяется правилом правой руки. Согните четыре пальца правой руки по направлению вращения. | |
| Тогда большой палец будет направлен по оси в направлении, совпадающим с направлением вектора 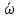 (рис. 1). Вектор углового ускорения (рис. 1). Вектор углового ускорения 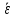 при ускоренном движении совпадает по направлению с вектором при ускоренном движении совпадает по направлению с вектором 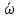 , а при замедленном движении противоположен ему. , а при замедленном движении противоположен ему. | ||
Если к телу с определенной осью вращения приложена сила, то вращающее действие этой силы зависит от ее величины, точнее, приложения и направления ее действия по отношению к оси. Вращающее действие силы характеризуется моментом этой силы М. Момент силы относительно данной оси численно равен произведению проекции силы F на плоскость, перпендикулярную к оси, на кратчайшее расстояние r между осью и точкой приложения силы.
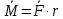 | (3) |
Вектор момента силы направлен по оси так, что, смотря на тело в направлении вектора
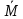 , мы видим вращение, проходящее по часовой стрелке (рис. 1). Момент силы равен нулю, если сила параллельна оси (F=0) или проходит через нее (r=0).
, мы видим вращение, проходящее по часовой стрелке (рис. 1). Момент силы равен нулю, если сила параллельна оси (F=0) или проходит через нее (r=0). Момент инерции
Момент инерции играет туже роль во вращательном движении, что и масса при движении по прямой. Чем больше момент инерции, тем больший требуется момент силы, чтобы изменить угловую скорость.
Момент инерции тела относительно данной оси – это мера инертности тела при вращении вокруг этой оси.
Момент инерции тела – скалярная величина. Нужно иметь ввиду, что эта величина существует безотносительно к вращению. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции относительно любой оси подобно тому, как тело обладает массой независимо от того, движется оно или находится в покое.
Значение момента инерции определяется не только массой тела, но и радиальным распределением массы. Если рассмотреть отдельную материальную точку массой m, вращающуюся вокруг оси на расстоянии r, то ее момент инерции равен:
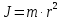 | (4) |
Если любое вращающееся тело разбить на малые элементы с массой
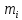 , вращающиеся вокруг оси на расстоянии
, вращающиеся вокруг оси на расстоянии 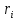 , то полный момент инерции тела относительно данной оси будет равен сумме моментов инерции отдельных малых элементов, из которых составлено тело:
, то полный момент инерции тела относительно данной оси будет равен сумме моментов инерции отдельных малых элементов, из которых составлено тело:
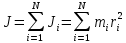
В случае непрерывного распределения масс эта сумма сводится к интегралу:
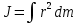 | (5) |
| В качестве примера найдем момент инерции однородного диска высотой h и радиусом 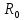 относительно оси, перпендикулярной плоскости диска и проходящей через его центр (рис. 2). Выразим в (5) массу через плотность: относительно оси, перпендикулярной плоскости диска и проходящей через его центр (рис. 2). Выразим в (5) массу через плотность: |  Рис. 2 |
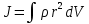 .
.Разобьем диск на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя
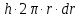 , поскольку диск однороден,
, поскольку диск однороден, 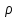 можно вынести за знак интеграла.
можно вынести за знак интеграла. 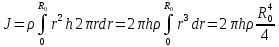
Выведем массу всего диска
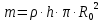 и получим:
и получим: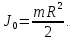
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси вращения равен сумме момента инерции J0 относительно параллельной оси, проходящей через центр масс тела и произведения массы тела m на квадрат расстояния
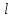 между осями:
между осями: 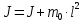 | (6) |
Момент силы, момент инерции относительно той же оси и угловое ускорение тела связаны основным законом динамики для вращательного движения, аналогичным второму закону Ньютона:
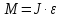 | (7) |
Этот закон можно записать в виде:
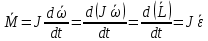 | (8) |
Вектор
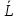 называется моментом импульса тела. Тело, вращающееся вокруг оси, обладает кинетической энергией:
называется моментом импульса тела. Тело, вращающееся вокруг оси, обладает кинетической энергией: 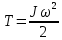 | (9) |
Принцип измерения и вывод рабочей формулы
Вращательное движение тела вокруг неподвижной оси описывается основным уравнением динамики вращательного движения (8).
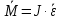 | (10) |
где
 – угловое ускорение;
– угловое ускорение;М – момент сил, действующих на тело;
J – момент инерции тела относительно оси.
Рассмотрим опыт, позволяющий на основании уравнения (10) определять момент инерции вращающегося тела. Схема опыта представлена на рис. 3. Тело вращения – маховик 1 со шкивом 2, укрепленный на горизонтальной оси. Вращающий момент сил создается грузом 3, привязанным к навитой на шкив нити:
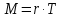 | (11) |
где Т – сила натяжения нити, r – радиус шкива.
На груз действует сила тяжести mg и сила натяжения нити, под действием которых он движется с ускорением a. Согласно второму закону Ньютона:
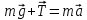 в проекциях на ось y:
в проекциях на ось y: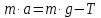
Или, преобразовав,
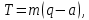 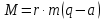 | (12) |
Если шнур разматывается без проскальзывания, то пройденное грузом расстояние
h связано с углом поворота шкива
 соотношением:
соотношением: 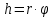 | (13) |
Продифференцировав (13) соответственно один и два раза по времени с учетом постоянства r, получим связь между линейной скоростью
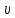 , ускорением груза, угловой скоростью
, ускорением груза, угловой скоростью 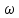 и ускорением маховика:
и ускорением маховика: 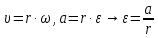 | (14) |
Подставив в (10) выражение для
 из (14) и для М из (4) и (12), получим:
из (14) и для М из (4) и (12), получим: 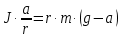 | (15) |
Из этого выражения видно, что для определения момента инерции маховика J необходим радиус вала r, масса груза m и ускорение движения груза a. Первые две величины могут быть измерены прямым путем, а ускорение – косвенным, через путь, проходимый грузом, и его время движения t. Учитывая, что начальная скорость груза равна нулю, запишем уравнение кинематики его поступательного прямолинейного движения:
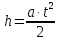 | (16) |
и выразим из этого уравнения ускорение a:
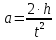 | (17) |
Подставляя (17) в уравнение (15), получим рабочую формулу для экспериментального определения момента инерции маховика через величины, измеряемые прямым путем: радиус вала r, массу груза m, время движения груза t, пройденный грузовой путь h и известную величину – ускорение свободного падения ≈ 10 м/с2.
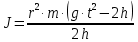 | (18) |
Эта же рабочая формула может быть выведена из энергетических представлений. Груз массой