ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 178
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени
Федеральное Государственное образовательное учреждение
Высшего профессионального образования
Московский Технический Университет Связи и Информатики
Кафедра общей теории связи
Индивидуальное задание
по дисциплине ТиИК
Вариант 23
Выполнил: студент группы ЗРС1901
0000000010110011100000001000100111100000111011110100000000 01001 0001001100100010001
Проверил: профессор Аджемов А.С.
Москва 2022
Индивидуальное задание:
1. Рассчитать оценку математического ожидания и дисперсии согласно варианту по номеру журнала. |+|
2. Рассчитать дифференциальную энтропию непрерывного источника согласно варианту по номеру журнала. |+|
3. Рассчитать среднее количество информации для дискретного источника, вырабатывающего зависимые сообщения согласно варианту по номеру журнала. |+|
4. Построить арифметический код слова согласно варианту по номеру журнала. |+|
5. Зашифровать фамилию и имя с помощью кода Цезаря. |+|
6. Сообщение, зашифрованное кодом Цезаря, зашифровать с помощью «Квадрата Виженера». |+|
7. Фамилию и имя, зашифрованные кодом Цезаря и затем Виженера, закодировать кодом Хаффмана. |+|
8. Провести расчет времени передачи изображения. |+|
9. Рассчитать параметры ИКМ преобразования согласно варианту по номеру журнала. |+|
10. Рассчитать «спектр искажений» при ИКМ преобразовании для заданного способа кодирования уровней (по номеру журнала) для однократных, двукратных и трехкратных ошибок. Рассчитать среднюю величину искажений при одиночных независимых ошибках, возникающих с вероятностью p =
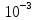. Рассчитать среднюю величину искажений, которую вносит однократная, двукратная и трехкратная ошибки. |Доделать|11. Рассчитать «спектр искажений» для
модели сообщений, соответствующих точкам, размещенных на плоскости, когда погрешность определяется квадратом геометрического расстояния между этими точками. Рассчитать среднюю величину искажений при одиночных независимых ошибках, возникающих с вероятностью p =
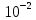. Рассчитать среднюю величину искажений, которую вносит однократная и двукратная ошибки. 1. Рассчитать оценку математического ожидания и дисперсии согласно варианту по номеру журнала.
| P(мВт) | 500 | 525 | 550 | 575 | 600 | 625 | 650 | 675 | 700 | 725 |
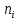 | 67 | 70 | 79 | 83 | 45 | 66 | 78 | 63 | 58 | 54 |
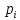 | 0,102 | 0,105 | 0,119 | 0,125 | 0,068 | 0,1 | 0,118 | 0,095 | 0,087 | 0,081 |
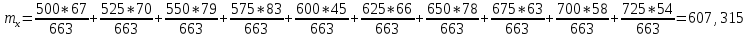
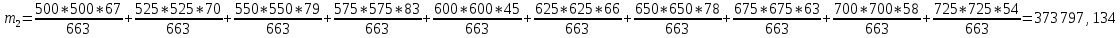
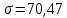
2. Рассчитать дифференциальную энтропию непрерывного источника согласно варианту по номеру журнала.
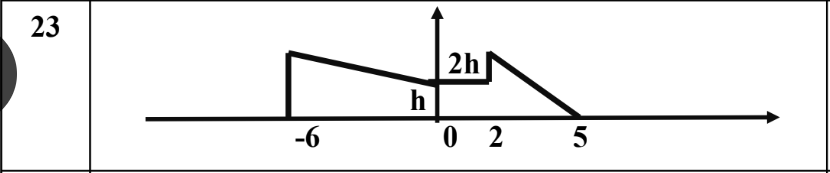
Нахождение площади под графиком:
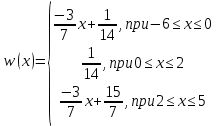
-6k+b=2/14
0+b=1/14
Искомая площадь:
; 
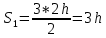= 3h/2*6 = 9hS =
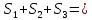3h + 2h + 9h = 14h
Площадь под графиком равна 1, исходя из этого находим h:
Вычислим интегралы:
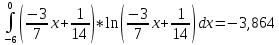
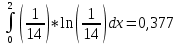
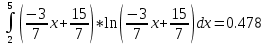
Суммируя проведенные вычисления, находим значение дифференциальной энтропии для непрерывного источника:
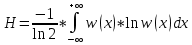
3. Рассчитать среднее количество информации для дискретного источника, вырабатывающего зависимые сообщения согласно варианту по номеру журнала.
Распределение вероятностей р(хk)
| Номер | х1 | х2 | х3 | х4 | |
| 23 | р(хk) | 0,125 | 0,375 | 0,25 | 0,25 |
Матрица условных вероятностей р(yj|xk)
| | y1 | y2 | y3 | y4 | y5 | y6 |
| x1 | 0,25 | 0,25 | 0,125 | 0,125 | 0,125 | 0,125 |
| x2 | 0,25 | 0,125 | 0,25 | 0,125 | 0,125 | 0,125 |
| x3 | 0,125 | 0,25 | 0,125 | 0,25 | 0,125 | 0,125 |
| x4 | 0,125 | 0,125 | 0,25 | 0,125 | 0,25 | 0,125 |
Построим вспомогательную таблицу, а для облегчения расчётов представим данные в виду правильных, а не десятичных дробей.
Таблица вероятностей р(xk, yj)
| | y1 | y2 | y3 | y4 | y5 | y6 |
| x1 |  | |  | | | |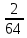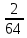
| x2 |  |  | | | | |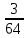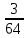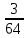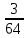
| x3 | |  | | | | |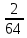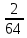
| x4 | | | | | | |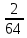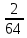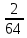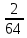
4. Построить арифметический код слова согласно варианту по номеру журнала.
Кодируемое слово: ТЕНТ_
| Слово | Xi | Yi |
| Т | 0,7 | 0,8 |
| ТЕ | 0,74 | 0,75 |
| ТЕН | 0,748 | 0,749 |
| ТЕНТ | 0,7487 | 0,7488 |
| ТЕНТ_ | 0,748700 | 0,748720 |
| n | Число | N=2n | Результат |
| 1 | 1 | 2 | 0,5 |
| 2 | 1*2+1=3 | 4 | 0,75 |
| 3 | 3*2-1=5 | 8 | 0,625 |
| 4 | 5*2+1=11 | 16 | 0,6875 |
| 5 | 11*2+1=23 | 32 | 0,71875 |
| 6 | 23*2+1=47 | 64 | 0,734375 |
| 7 | 47*2+1=95 | 128 | 0,7421875 |
| 8 | 97*2+1=191 | 256 | 0,74609375 |
| 9 | 191*2+1=383 | 512 | 0,748046875 |
| 10 | 383*2+1=767 | 1024 | 0,7490234375 |
| 11 | 767*2-1=1533 | 2048 | 0,74853515625 |
| 12 | 1533*2+1=3067 | 4096 | 0,7487752596875 |
| 13 | 3067*2-1=6133 | 8192 | 0,7486572265625 |
| 14 | 6133*2+1=12267 | 16384 | 0,74871826171875 |
(0,74871826171875(Т) – 0,7):0,1 = 0,4871826171875
(0,4871826171875(Е) – 0,4):0,1 = 0,871826171875