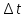Файл: Отчет принят оценка Ст преподаватель кафедры монгп т. А. Утемисов (подпись и дата).docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 29

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



«Уфимский государственный нефтяной технический университет»

Кафедра «Машины и оборудование нефтегазовых промыслов»

ОТЧЕТ ПРИНЯТ

Оценка ___________

Ст. преподаватель кафедры МОНГП

______________ Т.А. Утемисов

(подпись и дата)

Обработка информации о надежности буровых и нефтепромысловых машин

ОТЧЕТ

о практических занятиях

по дисциплине "Основы теории надежности"

Студент группы МП-18-01 Сафаров Д. В.

Уфа 2022


Содержание



Введение 3

Исходные данные. 5

1. Анализ статистического материала. 6

1.1 Построение вариационного ряда. 7

1.2 Построение статистического интервального ряда. 7

2. Расчет параметров статистического распределения. 9

2.1 Расчет математического ожидания. 9

2.2 Расчет дисперсии. 9

2.3 Определение среднеквадратического отклонения. 9

2.4 Расчет коэффициента вариации. 9

3. Оценка резко выделяющихся величин. 10

3.1 Оценка по критерию 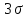. 10

3.2 Оценка по критерию Романовского. 10

3.3 Оценка по критерию Ирвина. 10

3.4 Оценка по критерию Граббса. 10

4. Расчет и построение графиков статистических функций. 13

4.1 Построение гистограммы дифференциальной функции. 13

4.2 Построение гистограммы интегральной функции. 14

4.3 Построение гистограммы функции интенсивности. 14

4.3 Построение гистограммы функции интенсивности. 15

5. Выбор теоретического закона распределения. 16

6. Расчет и построение теоретических функций. 19

6.1 Расчет дифференциальной функции распределения. 19

6.2 Расчет интегральной функции распределения. 20

6.3 Расчет обратной интегральной функции распределения. 21

6.4 Расчет функции интенсивности отказов. 22

7. Проверка гипотезы о соответствии эмпирического и теоретического распределения с помощью критериев согласия. 26

7.1 Критерий согласия К. Пирсона. 26

7.2 Критерий согласия А. Н. Колмогорова. 27

8. Определение границы доверительного интервалова показателя надежности. 28

Заключение 31

Список использованных источников 30

Подп. и дата



Инв. № дубл



Взам. инв. №



Подп. и дата



Инв. № подл.





















Лист



















Изм.
Лист
№ докум.
Подпись
Дата








Введение
Нагрузки, действующие на детали, агрегаты буровых и нефтегазопромысловых машин во время эксплуатации носят случайный характер. Случайными являются также характеристики материалов, конкретное значение которых зависит от множества факторов. Примерами случайной величины являются наработка на отказ, интенсивность отказов, технический ресурс, срок службы машины и т.д.

Совокупность значений случайной величин, расположенных в возрастающем порядке с указаниями вероятностей их появлений, называют распределением случайных величин. Соотношения устанавливающие связь между возможными, значениями случайной величины и соответствующим им вероятностями, называют законом распределения. Законы распределения могут задаваться аналитически, в виде графиков или таблиц.

В теории надежности используются разнообразные законы распределения. Задача теории надежности заключаются в выборе такого закона распределения, который наиболее полно отражает происходящий физический процесс. Подобрав теоретический закон распределения, решают практические задачи по определению показания надежности машин.

Для УЭЦН и нефтегазовых машин очень характерно рассеивание значений показателей надежности. Наряду с особенностями конструкции машин, технологией их изготовления большое влияние на разброс показателей надежности оказывают условия эксплуатации техники.

Под условиями эксплуатации понимаются климатические условия, квалификации обслуживающего персонала, состояние ремонтной базы, режим работы, особенности хранения оборудования, обеспеченность запасными частями, горюче-смазочными материалами и т.д. На глубинное оборудование значительные влияние оказывают угол искривления скважины, в которой эксплуатируется оборудование, ее глубина. Очень специфичны и разнообразны нагрузки, действующие на буровые и нефтегазопромысловые машины. В связи с этим статистическая информация должна отражать особенности режимов работы и условиях эксплуатации машин.

Подп. и дата



Инв. № дубл



Взам. инв. №



Подп. и дата



Инв. № подл.





















Лист



















Изм.
Лист
№ докум.
Подпись
Дата








Требуется обработать результаты пассивных экспериментов методом математической статистики. По обработанным данным выбрать теоретический закон распределения, и по выбранному закону предложит влияющий фактор на надежность, также определить показатели надежности трубобура, т.е. свойства объекта непрерывно сохранять работоспособное состояние до наступления предельного состояния, а также приспособленность к предупреждению и обнаружению отказов путем обслуживания.

Обработка статистической информации о надежности ведется в следующей последовательности:

- Анализ статистического материала и построение статистического ряда информации;

- Расчет параметров статистического распределения;

- Оценка резко выделяющихся величин;

- Построение эмпирического и теоретического показателя надежности;

- Выбор теоретического закона распределения;

- Проверка гипотезы о соответствии эмпирического и теоретического распределения с помощью критериев согласия;

- Определение доверительных границ показателя надежности.

Подп. и дата



Инв. № дубл



Взам. инв. №



Подп. и дата



Инв. № подл.





















Лист



















Изм.
Лист
№ докум.
Подпись
Дата








Исходные данные
№ 34 Наработка до отказа турбобура, ч.:

63, 31, 57, 92, 2, 80, 44, 65, 97, 87, 48, 22, 95, 76, 3, 82, 54, 26, 50, 71, 6, 92, 36, 59, 70, 28, 35, 46, 67, 39, 90, 52, 17, 63, 93, 4, 79, 25, 91, 82, 7, 47, 75, 67, 83, 19, 58, 73, 89, 62, 53,

п=65

№ 31

Наработка до отказа турбобура, ч.:

21, 127, 3, 31, 67, 51, 8, 33, 42, 10, 58, 24, 33, 102, 25, 124, 21, 34, 66, 31, 17, 2, 85, 46, 16, 7, 76, 107, 116, 2, 3, 78, 24, 27, 84, 10, 22, 18, 97, 28, 47, 8, 44, 24, 55, 53, 70, 9, 24, 76, 35, 51, 11, 13, 16, 71, 96, 70, 56, 31, 21, 49, 33, 59, 71, 43 ,

п=66








1. Анализ статистического материала.
Таблица №1 Рабочая таблица (распределение наработки до отказа трубобура по оси времени).


ti
Частота ni
ti
Частота ni
ti
Частота ni
ti
Частота ni

1



35
||
69



103



2
|||
36
|
70
|||
104



3
|||
37



71
|||
105



4
|
38



72



106



5



39
|
73
|
107
|

6
|
40



74



108



7
||
41



75
|
109



8
||
42
|
76
|||
110



9
|
43
|
77
|
111



10
||
44
||||
78
|
112



11
|
45



79
|
113



12



46
||
80
|
114



13
||
47
||
81



115



14



48
|
82
|||
116
|

15



49
|
83
|
117



16
||
50
|
84
|
118



17
||
51
||
85
|
119



18
|
52
|
86



120



19
||
53
||
87
|
121



20



54
||
88



122



21
|||
55
|
89
|
123



22
||
56
|
90
|
124
|

23



57
|
91
|
125



24
|||||
58
||
92
||
126



25
||
59
||
93
||
127
|

26
|
60



94
|






27
|
61



95
|






28
|
62
|
96
|






29



63
||
97
||






30



64



98









31
||||
65
|
99









32



66
|
100









33
|||
67
|||
101









34
|
68



102
|







n = 65
ti - наработка трубобура до отказа;

ni* - частота.



Подп. и дата



Инв. № дубл



Взам. инв. №



Подп. и дата



Инв. № подл.





















Лист



















Изм.
Лист
№ докум.
Подпись
Дата








1.1 Построение вариационного ряда.
Построение вариационного ряда путем ранжирования наработку турбобура до отказа.
Таблица № 2 Вариационный ряд


1
2
4
4
5
6
6
12
12
14
17
17

19
21
21
27
29
30
30
33
35
36
36
39

41
43
44
45
46
46
49
50
52
56
57
57

60
60
62
62
63
64
65
67
72
76
77
78

78
78
78
82
87
93
97
98
99
102
113
117

119
124
124



























n = 63
1.2 Построение статистического интервального ряда.
Вычисляем число интервалов k
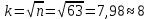
Вычисляем величину интервалов

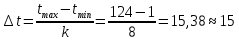
Таблица №3 Статистический интервальный ряд


Интервал, ч
Середина интервала ti , ч
Частота n*i
Опытная вероятность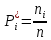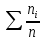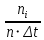





0...15
7,5
10
0,1587
0,1587
0,0105

15...30
22,5
7
0,1111
0,2698
0,0074

30...45
37,5
10
0,1587
0,4285
0,0105

45…60
52,5
9
0,1428
0,5713
0,0095

60...75
67,5
9
0,1428
0,7141
0,0095

75...90
82,5
8
0,1269
0,841
0,0084

90...105
97,5
5
0,0793
0,9203
0,0052

105...120

120
5(3+2)
0,0793
0,9996
0,0052

120...135

n = 63
Поскольку частота в интервалах 105...120; 120...135 меньше 5, то необходимо объединить эти интервалы. И следовательно еще рас построить статистический ряд


3.3 Оценка по критерию Ирвина.
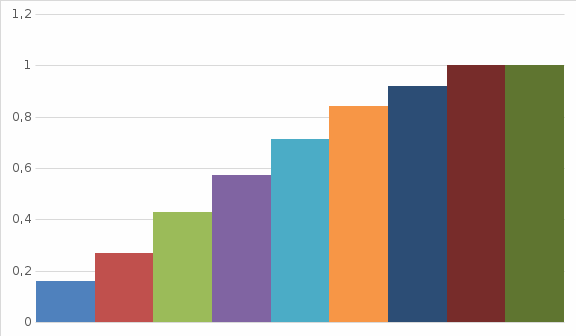
Определяют критерий λ по формуле ,

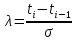где 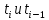смежные точки информации.
Если 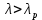при n = 63 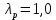, то данный результат можно исключить из дальнейшего рассмотрения, где ti и ti-1 смежные точки информации.

Проверим 124: 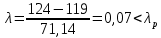, так как 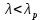, то нет необходимости исключать эту величину.

Проверим 119: 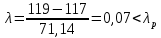, так как 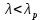, то нет необходимости исключать эту величину.


4.2 Построение гистограммы интегральной функции.
Рисунок № 2 Гистограмма интегральной функции распределения F(t)


F(t)


0,1587

0,2698

0,4285

0,5713

0,7141

0,841

0,9203

0,9996

15

30

45

60

75

90

105

120

135


Смотрите также файлы