Файл: Отчет принят оценка Ст преподаватель кафедры монгп т. А. Утемисов (подпись и дата).docx
Добавлен: 23.11.2023
Просмотров: 30
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
6. Расчет и построение теоретических функций.
6.1 Расчет дифференциальной функции распределения.
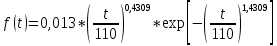
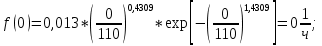
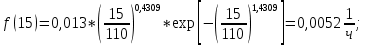
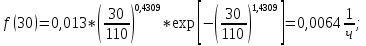
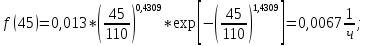
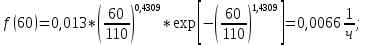
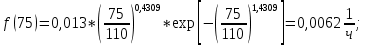
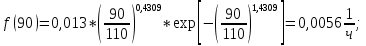
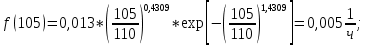
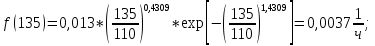
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
| | | Проверка полученного значения критерия согласия по Д.Письменному: Критерий согласия является верным если 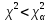 по степени свободы по степени свободы r = k – s. где k– число интервалов s – число обязательных связей Для нормального закона и распределения Вейбулла s=3 , поэтому число интервалов статистического ряда при применении критерии К.Пирсона должно быть k >4. Критерий К.Пирсона применяют при числе наблюдений n>30. В каждом интервале рекомендуется иметь не менее 5-10 значений случайной величины. Допускается объединять интервалы , если ni <5. r = 8 - 3 = 5; при r = 5, 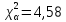 Следовательно 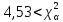 . .Определим вероятность совпадения эмпирического и теоретического распределения: 4,03 - 0,5 2,03 - 100% 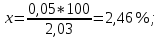 0,05 - x% 6,06 - 0,3 Тогда 0,5 - 0,3 = 0,2 0,2 - 100% x - 2,46% 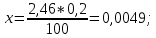 p = 0,5 - 0,0049 = 0,4951 Вероятность совпадения теоретической и эмпирического распределения 49,51% | ||||||
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
| | | 7.2 Критерий согласия А. Н. Колмогорова. |Dmax| = 0,9959; 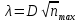 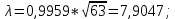 Находим P(λ) методом интерполяции: λ P(λ) 7,9 0,0028 8,0 0,0027 0,1 - 100% 0,9959 - x% 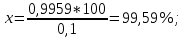 Тогда 0,0028- 0,0027= 0,0001 0,0001 - 100% x - 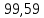 % % 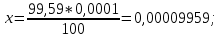 P(λ) = 0,964 – 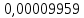 = 0,9639 = 0,9639Таким образом гипотеза не отвергается. 8. Определение доверительного интервала показателя надежности. Доверительные границы указывают , в каких пределах с заданной доверительной вероятностью может изменятся одиночный показатель надежности . Доверительные границы рассеивания среднего значения при распределении Вейбулла равны: 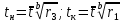 b = 1,4403. b = 1,4403. Значения r3 и r1 определяем по таблицам значения r3 и r1, при γ = 0,95; n = 65. | ||||||
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
| | | Определим tк: n r1 60 1,25 80 1,21 20 - 100% 3 - x% 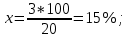 Тогда 1,25 - 1,21 = 0,04 0,04 - 100% x - 15% 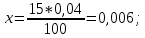 r1 = 1,25 - 0,006 = 1,244; 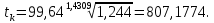 Определим tн: n r3 60 0,82 80 0,84 20 - 100% 3 - x% 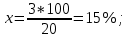 Тогда 0,84 - 0,82 = 0,02 0,02 - 100% x - 15% 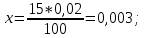 r3 = 0,84 - 0,003 = 0,837; 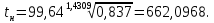 Доверительный интервал показания надежности 662,0968...807,1774 объяснятся значительным объемом информации n = 65. При меньших значениях n доверительный интервал t̄ был бы более широким. | ||||||
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
| | | Заключение Закон распределения наработки до отказа трубобура подчиняется распределению Вейбулла. Параметр формы b = 1,4403; параметр масштаба a = 45. Значение коэффициента вариации V = 0,69, значит пределы изменения коэффициента вариации 0,5 - 0,7. Определяющие факторы вида распределения ресурса машин и сборочных единиц: Доминирующий характер разрушения - усталостное разрушение; Условия эксплуатации - изменяющиеся в широких пределах; Режим нагрузки - средние нагрузки; Условия технического изготовлений - средний. | ||||||
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
| | | Список использованных источников. 1. Бабаев С.Г. Надежность нефтепромыслового оборудования / С.Г. Бабаев. - М.: Недра, 1987.- 264 с.: ил. 2 Решетов Д.Н. Надежность машин: Учебное пособие для машиностроительных специальностей вузов / Д.Н. Решетов, А.С. Иванов, В.З. Фадеев; под ред. Д.Н. Решетова. - М.: Высш. шк., 1988. - 238 с.: ил. 3 Кубарев А.И. Надежность в машиностроении / А.И. Кубарев.- 2-е изд., перераб. и доп.- М.: Изд-во стандартов, 1696. - 224 с.: ил. 4 Острейковский В.А. Теория надежности: Учебник для вузов / В.А. Острейковский. - М.: Высш. шк., 2003. - 463 с.: ил. 5 Гмурман В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман.- М.: Высш. ш.„ 1997. 6 Гмурман В.Е. Руководство к решению задач по теории вероятности и математической статистике / В.Е. Гмурман.- 3-е изд„ перераб. и доп.- М Высш. шк., 1979. - 400 с.: ил. 7 Писменный Д.Т. Конспект лекций по теории вероятностей и математической статистике / Д. Т. Писменный .- М.: Айрис- пресс, 2004.- 256 с.: ил. 8 Венцель Е. С. Теория вероятностей / Е.С. Венцель .- М.: Наука, 1964. 9 Обработка информации о надежности буровых и нефтепромысловых машин: Учеб.-метод. пособие для студентов спец. 130503 и 130602 / УГНТУ: каф. НГПО; сост. И.Е. Ишемгужин, В.В. Шайдвков, Е.И. Ишемгужин.- Уфа: Изд-во УГНТУ, 2007… 39 с. | ||||||
| Подп. и дата | | |||||||
| Инв. № дубл | | |||||||
| Взам. инв. № | | |||||||
| Подп. и дата | | |||||||
| Инв. № подл. | | |||||||
| | | | | | | Лист | ||
| | | | | | | |||
| Изм. | Лист | № докум. | Подпись | Дата | ||||
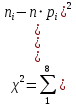
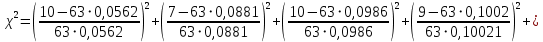
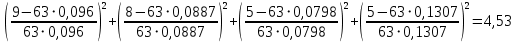
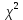 в зависимости от числа эмпирического и теоретического распределений. Если найденная вероятность p> 0,1 , то считают, что статистические данные не противоречат принятому теоретическому распределению. При вероятности совпадения меньше, чем 0,1 считается , что следует подобрать более подходящий закон распределения.
в зависимости от числа эмпирического и теоретического распределений. Если найденная вероятность p> 0,1 , то считают, что статистические данные не противоречат принятому теоретическому распределению. При вероятности совпадения меньше, чем 0,1 считается , что следует подобрать более подходящий закон распределения.