Файл: национальный исследовательский томский политехнический универсистет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 44
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Институт – ИШНКБ
Направление – Электроника и наноэлектроника
Кафедра – ОЭИ
Лабораторная работа 1
Гармонический анализ периодических сигналов
Дисциплина Теория ЦОС
Вариант 7
| Исполнитель: | | ||||
| студент группы | 1А01 | | Левшин М.А. | | |
| | | | | | |
| Руководитель: | | ||||
| преподаватель | | | Кулагин А.Е. | | |
| | | | | | |
Томск 2022
Цель работы
Определить коэффициенты ряда Фурье и построить аппроксимирующую функцию для периодического сигнала, образованного из импульсов заданной формы.
Выполнение работы
-
Были найдены значения коэффициентов a0, an, bn разложения в ряд Фурье периодической последовательности прямоугольных импульсов (рис. 1.1) и рассчитаны значения An, ϕn первых пяти гармоник для произвольных T, τ. Все расчеты производились в программе MathCAD.

Рисунок 1.1 – Последовательность прямоугольных импульсов

Рисунок 1.2 – Заданные постоянные значения

Рисунок 1.3 – Рассчитанные значения коэффициентов a0, an, bn

Рисунок 1.4 – Рассчитанные значения An, ϕn первых пяти гармоник

Рисунок 1.5 – Фазовая спектральная диаграмма

Рисунок 1.6 – Амплитудная спектральная диаграмма
Также был построен график аппроксимирующего сигнала

Рисунок 1.7 – Аппроксимирующий сигнал

Рисунок 1.8 – График аппроксимирующего сигнала
Определенная по графику ошибка аппроксимации, возникающая из-за эффекта Гиббса, составляет 6,7%
2. Далее была сформирована математическая модель периодического сигнала x(t), заданного для каждого варианта. Также был построен график сигнала.

Рисунок 2.1 – Сигнал x(t), заданный вариантом

Рисунок 2.2 – математическая модель сигнала в программе MathCAD

Рисунок 2.3 – Построенный график сигнала x(t)
3. Далее были составлены выражения для расчета коэффициентов a0, an, bn, An, ϕn ряда Фурье для сигнала
x(t). Были рассчитаны значения этих коэффициентов. По полученным данным были построены амплитудная и фазовая спектральные диаграммы.

Рисунок 3.1 – Выражения для расчета коэффициентов a0, an, bn, An, ϕn
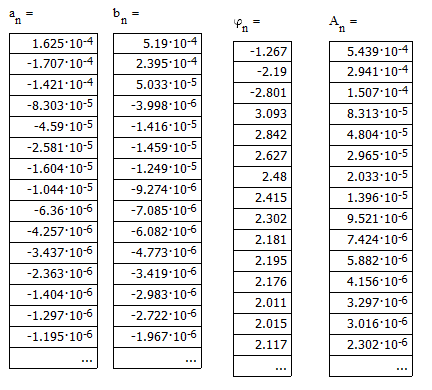
Рисунок 3.2 – Рассчитанные значения коэффициентов

Рисунок 3.3 – Фазовая спектральная диаграмма сигнала x(t)

Рисунок 3.4 – Амплитудная спектральная диаграмма сигнала x(t)
-
Далее был образован аппроксимирующий сигнал L(t). Были построены графики исходного и аппроксимирующего сигналов для N = 5, N = 10, N = 20 первых гармоник.
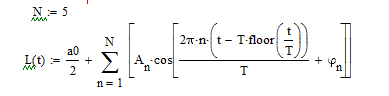
Рисунок 4.1 – Аппроксимирующая функция
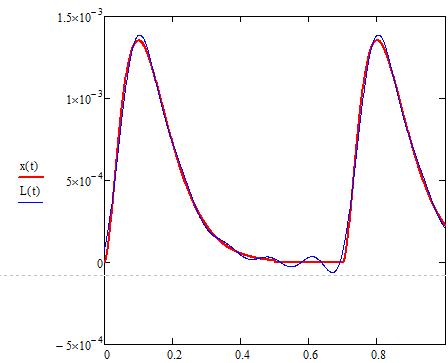
Рисунок 4.2 – Исходный x(t) и аппроксимирующий L(t) сигналы при N=5

Рисунок 4.3 – Исходный x(t) и аппроксимирующий L(t) сигналы при N=10

Рисунок 4.4 – Исходный x(t) и аппроксимирующий L(t) сигналы при N=20
Вывод: на графиках, изображенных на рисунках 3.2, 3.3, 3.4, можно увидеть, что, чем больше гармоник используются в аппроксимированном сигнале, тем меньше ошибка аппроксимации и тем сильнее аппроксимированный сигнал приближается к исходному.
5. Далее были построены графики сигналов ошибки ɛ(t) = x(t) – X(t) для N = 5, N = 10, N = 20.

Рисунок 5.1 – График сигналов ошибки для N = 5

Рисунок 5.2 – График сигналов ошибки для N = 10

Рисунок 5.3 – График сигналов ошибки для N = 20
Полученные результаты подтверждают выводы предыдущего пункта.
6. Далее были рассчитаны значения средней квадратической ошибки для N = 5, N = 10, N = 20.

Рисунок 6.1 – Средняя квадратическая ошибка для N = 5

Рисунок 6.2 – Средняя квадратическая ошибка для N = 10

Рисунок 6.3 – Средняя квадратическая ошибка для N = 20
По полученным результатам можно сделать вывод: увеличение числа используемых гармоник уменьшает величину средней квадратической ошибки.
7. Далее была рассчитана средняя мощность сигнала x(t), а также исследуемая мощность периодического сигнала, описываемого усеченным рядом Фурье, для N = 5, N = 10, N = 20.

Рисунок 7.1 – Средняя мощность сигнала x(t), для N = 5

Рисунок 7.2 – Мощность периодического сигнала x(t), для N = 5

Рисунок 7.3 – Мощность периодического сигнала x(t), для N = 10

Рисунок 7.4 – Мощность периодического сигнала x(t), для N = 20
Судя по полученным результатам, можно сделать вывод, что при увеличении числа гармоник значение средней мощности смоделированного сигнала стремится к значению средней мощности заданного сигнала.
Вывод: в ходе данной работы была построена математическая модель периодического сигнала, а также его разложение в ряд Фурье. Полученные данные говорят о том, что увеличение числа гармоник в аппроксимируемом сигнале приближают его к исходному. При этом уменьшается величина средней квадратической ошибки, которая стремится к нулю с уменьшением числа гармоник. По результатам расчетов можно увидеть
, что значение средней мощности смоделированного сигнала стремится к значению средней мощности заданного сигнала. Также, на графике аппроксимирующего сигнала мы можем пронаблюдать эффект Гиббса – появление пульсаций некоторой амплитуды в окрестности скачкообразного изменения сигнала, то есть точки разрыва первого рода.