Лекция. Основной закон зацепления. Элементы эвольвентного цилиндрического прямозубого колеса. Размеры эвольвентных зубчатых колес. Цилиндрическая передача Новикова.

В практике машиностроения нашли широкое применение зубчатые передачи, предназначенные для передачи энергии из одной точки пространства в другую, расположенную на некотором расстоянии от первой.





При этом зубчатые передачи должны обеспечить при заданном значении скорости вращения входных звеньев должны требуемые величины скоростей вращения выходных валов по величине и направлению. Эти условия могут быть реализованы только при определенной геометрии зубчатых колес.

Так как зубчатая передача относится к передаче зацепление зубьев зубчатых колес, то выполнение указанных условий связано с теорией их зацепления. Рассмотрим основной закон зацепления двух профилей звеньев, образующих высшую кинематическую пару.

Теорема Виллиса, которая носит название основного законазацепления,может быть сформулирована так: общая нормаль, проведенная через точку касания двух профилей, делит межосевое расстояние на части, обратно пропорциональные угловым скоростям.

Доказательство. Пусть имеем два рычага, которые касаются друг друга в точке В.



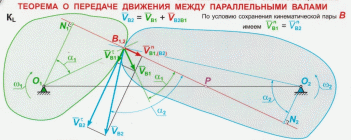
Рычаг 1 поворачивается вокруг центра О₁ по ходу движения часовой стрелки, давит на рычаг 2, который вследствие этого поворачивается вокруг центра О₂ против движения часовой стрелки. Через точку касания В проведем общую нормаль N₁N₂, которая пересечет линию центров О₁О₂ в точке Р. Требуется доказать, что расстояние РО₁ и РО₂ пропорциональны угловым скоростям, т.е.

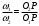. (1)

Для доказательства соединим точку В с центрами вращения О₁ и О₂. Отрезок О₁В будет радиус вращения точки касания первого рычага

---

, а О₂В радиус вращения точки касания второго рычага. Перпендикулярно радиусам вращения отложим скорости V_B1 и V_B2 и разложим их на составляющие по общей нормали N₁N₂ через 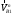и 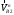, и составляющие по общей касательной – через 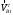и .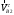

Нормальные составляющие скоросте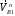й и 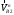должны быть равны друг другу. Это заключение делаем из следующих соображений. Если 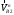больше, чем 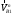, то произойдет отрыв профилей друг от друга, что недопустимо для зубчатого зацепления. Если же 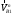будет больше 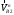, то рычаг 1 должен внедрится в тело рычага 2, т.е. должно произойти разрушение, что тоже недопустимо, следовательно .

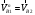Касательные составляющие скоросте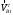й и 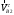могут быть неравными. Разность между ними будет обуславливать величину скольжения профилей друг по другу.

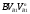
Из центров вращения О₁ и О₂ на общую нормаль N₁N₂ опускаем перпендикуляры О₁N₁ и О₂N₂. Возьмем два треугольника О₁N₁В и 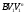, которые подобны, так как стороны их перпендикулярны. Из подобия этих треугольников можно записать пропорцию:

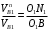. (2)

Откуда имеем:

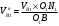. (3)

Аналогично из подобия треугольников О₂N₂В и 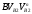можно записать пропорцию: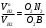

---

. (4)

Откуда имеем:

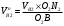. (5)

Но нормальные составляющие скоростей (как выяснено выше) должны быть равны друг другу. Следовательно,
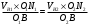. (6)

Выразим скорости через угловые скорости:

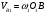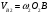и . (7)

Подставляя эти значения в уравнение (6), получим:

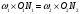. (8)

Перепишем это уравнение в виде пропорции:

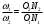. (9)

Из подобия треугольников O₁N₁Pи O₂N₂P следует, что

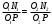, (10)

или

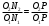. (11)

Подставляя в формулу (9) вместо 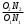отношение 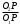, получим:



Что и требовалось доказать.

Отношение угловых скоростей есть передаточное отношение:



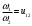
На основании теоремы Виллиса можно сделать заключение, что для постоянства передаточного отношения нужно, чтобы нормали, проведенные через точки касания, пересекли межосевое расстояние в постоянной точке.

Тачка пересечения общей нормали с межосевым расстоянием называется полюсом зацепления (точка Р).

Для зубчатого колеса окружность, проходящей через полюс зацеплением (следовательно, имеющая радиус, равный расстоянию от центра колеса до полюса зацепления) называется начальной.

Основной закон зацепления позволяет выяснить, какие кривые могут служить профилями зубьев со строго постоянным передаточным отношением. В самом деле, ведь в зацеплении, все нормали к кривым, проведенные через точку касания профилей, должны проходить через полюс зацепления, т.е. должны пересекаться в одной точке.

Этим свойством обладают только кривые, относящие к семейству рулет. Рулетами называются кривые, которые описываются точками, скрепленными с кривой, катящейся по другой неподвижной кривой. Самыми простыми кривыми, относящиеся к семейству рулетт, являются циклоидные кривые (эпициклоида и гипоциклоида) и эвольвента.

---

Эти кривые и используются в качестве профилей зубьев. Сначала появилось циклоидное зацепление. В циклоидном зубчатом колесе профиль головки зуба очерчивается по эпициклоиде, а профиль ножки зуба – по гипоциклоиде.

В 1764 г. Эйлер предложил эвольвентное зацепление. В эвольвентных зубчатых колесах профили зубьев очерчиваются по эвольвентам окружности с центром на оси колеса. Если на окружность положить прямую линию, на которой зафиксирована некоторая точка S, и без скольжения обкатывать прямую по окружности в ту или другую сторону, то данная точка на плоскости будет очерчивать кривую, названную эвольвентой.


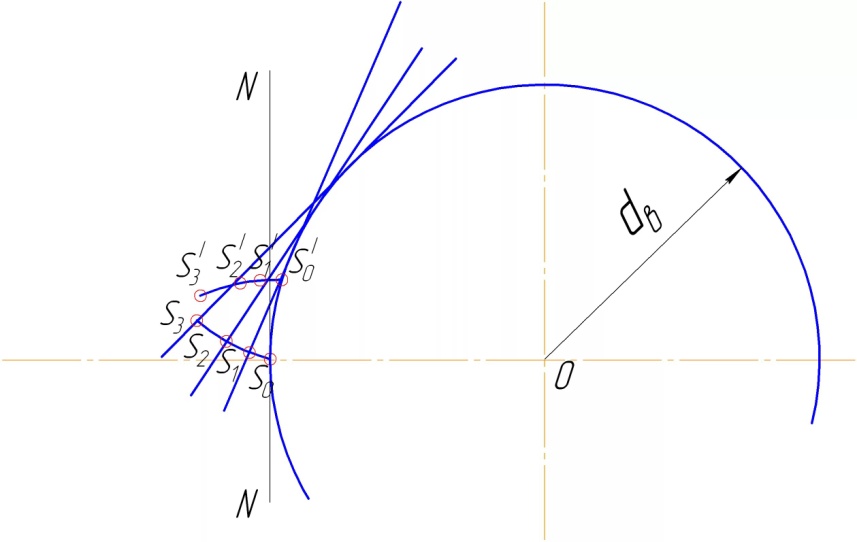
В настоящее время применяется почти исключительно эвольвентное зацепление, поскольку по сравнению с циклоидным зацеплением обладает меньшим контактным напряжением а, следовательно, меньшим износом, т.е. большей долговечностью.

Кроме того, эвельвентное зацепление допускает некоторое изменение межосевое расстояние (радиальный зазор), не нарушая закон зацепления, т.е. не требует большой точности при сборке. Преимуществом эвольвентного зацепления является возможность иметь сменные шестерни. Если необходимо изменить передаточное отношение, то при циклоидном зацеплении надо заменить оба зубчатых колеса, а при эвельвентном зацеплении - только одно.
Прямозубое цилиндрическое эвольвентное зубчатое колесо представляет собой цилиндр, по образующей которого расположены выступы (зубья). Поверхность, отделяющая зубья от тела зубчатого колеса, называется поверхностью впадин зубьев. Поверхность, ограничивающая зубья со стороны, противоположной телу зубчатого колеса, - поверхность вершин зубьев. Пространство между двумя соседними зубьями – впадина. Поверхность, ограничивающая зуб со стороны впадины, называется боковой поверхностью зуба.


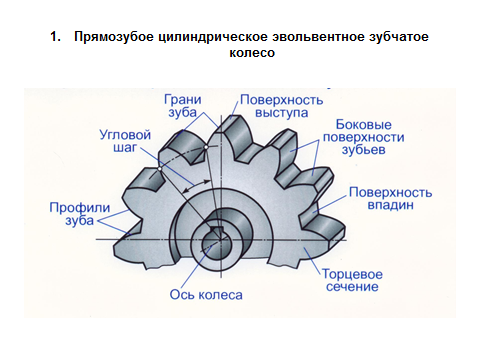
Рис.1


Рис. 2

Окружность, ограничивающая зубья с внешней стороны, называется окружностью вершин зубьев диаметром d_a. Окружность, ограничивающая зубья с внутренней стороны, называется окружность впадин зубьев диаметром d_f. Окружность диаметром d_b, определяющая эвольвентный профиль зуба, называется

---

основной окружностью.

Геометрическое место точек касания двух профилей зубчатых колес (непрерывная линия красного цвета) называется линией зацепления.


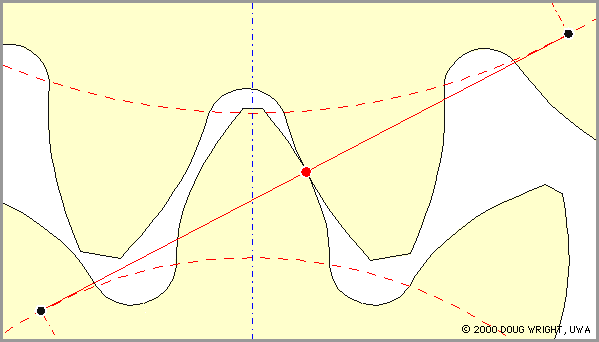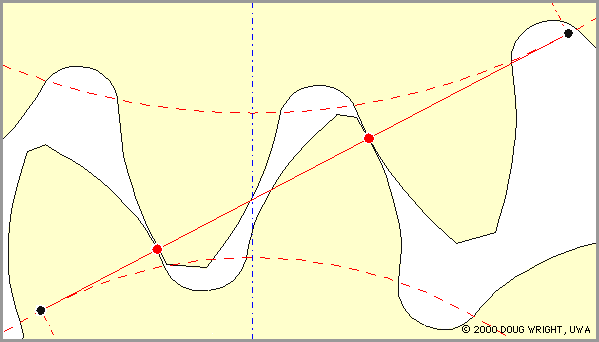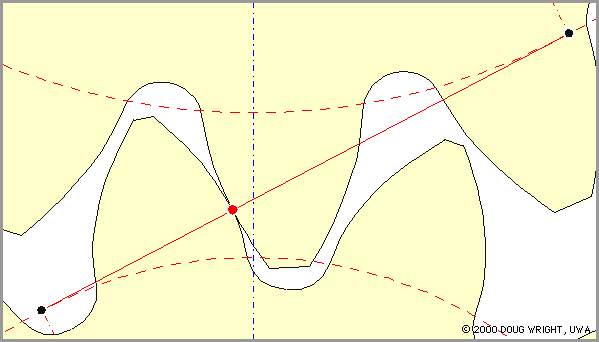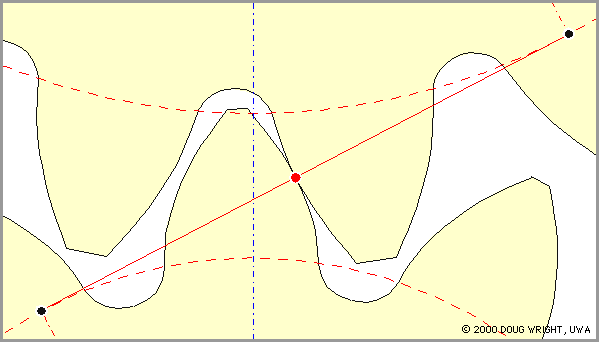
Рис. 3
Выясним, что представляет собой линия зацепления при работе зубьев с эвольвентным профилем.

Если через произвольную точку касания двух профилей проведем общую нормаль, то она, согласно основному закону зацепления, пройдет через полюс зацепления Р и будет наклонена к общей касательной начальных окружностей под углом зацепления 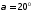, названный углом зацепления.

Отрезок, заключенный между перпендикулярами, опущенные на линию зацепления из центров вращения зубчатых колес, называется теоретической линией зацепления (на рис. Непрерывная линия красногоцвета).
Действительная линия зацепления представляет собой отрезок прямой, заключенный между началом и концом зацепления. Начало и конец зацепления – это точки пересечения окружностей вершин зубьев с линией зацепления.



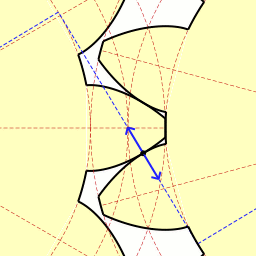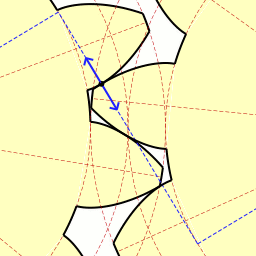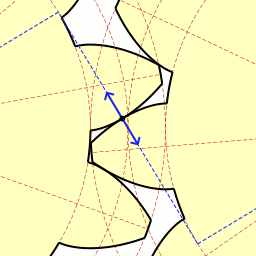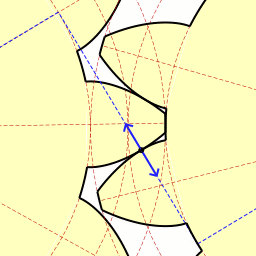
Рис. 4
Примечание. Для наглядности перенесите предложенную картинку в презентацию MicrosoftPowerPoint.
Эвольвента – кривая, у которой непрерывно меняется кривизна, причем центры кривизны ее находятся на основной окружности, а радиусами кривизны являются касательными к основной окружности.

Межосевое расстояние – кратчайшее расстояние между осями зубчатых колес.

Полюс зацепления – точка пересечения линии зацепления с межосевой линией.

Начальная окружность – окружность, центр которой находится в центре зубчатого колеса и касается в полюсе зацепления. Начальные окружности в процессе зацепления двух профилей обкатываются друг по другу без скольжения, т.е. линейные скорости точек, лежащих на обеих начальных окружностях одинаковы.

Шаг зацепления Р – длина дуги окружности между одноименными точками двух соседних зубьев. Шаг может быть измерен по окружности любого радиуса.

Длина дуги окружности, приходящейся на один зуб, называется толщиной зуба. Длина дуги окружности в пределах впадины зуба называется шириной впадины.

---

Смотрите также файлы

• Денсаулыты ныайтуа байланысты жаттыу трлерімен танысады.docx

• Вариант 21 Задание 1 Определение водопритока в вертикальный ствол шахты Условие задачи.docx

• Программа художественной направленности Волшебная радуга.pdf

• А. Г. Решетников марта 2022 г.docx

• Оценка эффективности использования основных фондов строительного предприятия.docx