Шаг равен сумме толщины зуба и ширины впадины.
Из всех размеров зубчатого колеса обычно один принимается за основной (этот размер вводят в расчетные формулы на прочность) и через него выражают все остальные размеры. Сначала за основной размер был принят шаг зацепления. Зубчатые колеса, за основной размер был принят шаг зацепления, назывались шаговыми. Но очень скоро выяснилось, что шаг зацепления неудобен как основной размер, так как шаговые колеса не могут иметь диаметров, выраженных круглыми числами. В самом деле, если шаг зацепления, измеренный по начальной окружности, умножить на число зубьев, то получим длину начальной окружности:

,

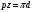Откуда диаметр начальной окружности:

.

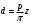Если шаг и число зубьев целые числа, то диаметр d – число иррациональное (в формуле присутствует иррациональное число 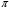). От шага как основного размера отказались, и сейчас шаговые колеса не производятся ни в одной стране. В настоящее время почти во всех странах (кроме Англии и США) за основной размер принята величина в «пи» раз меньше шага зацепления, которая называется модулем зацепления, и обозначается через m:

.

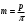Зубья зубчатых колес нарезаются зубонарезными инструментами с определенным модулем. Для уменьшения количества нарезаемого инструмента числовые значения модуля ограничили и стандартизовали (ГОСТ 9563-60):

. . . ,1; 1,25; 1,5; . . . и т.д.

Делительной окружностью (d) называется окружность, диаметр которой равен произведению модуля на число зубьев:

.
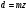Размеры зубчатого колеса приведены в таблице.

Диаметр делительной окружности: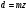
Высота головки зуба:	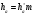где 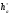- коэффициент высоты зуба.
Высота ножки зуба:	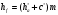где 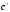- коэффициент радиального зазора.
Высота зуба: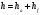
Шаг зацепления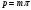
Диаметр окружности вершин зубьев: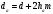
Диаметр окружности впадин зубьев: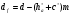
Толщина зуба по делительной окружности: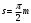
Ширина впадины по делительной окружности: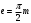
Межосевое расстояние: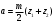

---

Принятые в машиностроении величины

	Нормальный зуб	Укороченный зуб
	1	0.8
	0.25	0.3

В Англии и США за основной размер зубчатых колес принята величина, обратная модулю, т.е. отношение числа зубьев к диаметру делительной окружности. Эта величина называется питчем.

Внешнее эвольвентное зацепление, несмотря на ряд достоинств (простота изготовления, нечувствительность к изменению межосевого расстояния и т.д.), имеет существенный для тяжело нагруженных передач недостаток. Заключающийся в том, что зубья касаются выпуклыми поверхностями. Для уменьшения контактных напряжений надо, чтобы выпуклая поверхность одного зуба касалась вогнутой поверхности другого зуба. Такое касание имеют эвольвентные зубья при внутреннем зацеплении и зубья, профили которых очерчены по гипоциклоиде и эпициклоиде (циклоидное зацепление). Еще более благоприятный контакт получается у зубьев, профили которых по предложению М.Л. Новикова в торцевой плоскости очерчены по дугам окружностей с почти равными радиусами.

Вопросы для самоконтроля.
1. Какая окружность называется начальной?

2. Что понимается под модулем зацепления?

2. Какая окружность называется делительной?

4. По какой окружности толщина зуба равна ширине впадины?

5. Какое зацепление относится к зацеплению Новикова?

---

Смотрите также файлы

• Денсаулыты ныайтуа байланысты жаттыу трлерімен танысады.docx

• Вариант 21 Задание 1 Определение водопритока в вертикальный ствол шахты Условие задачи.docx

• Программа художественной направленности Волшебная радуга.pdf

• А. Г. Решетников марта 2022 г.docx

• Оценка эффективности использования основных фондов строительного предприятия.docx