ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ
ЛАБОРАТОРНАЯ РАБОТА
ПО ФИЗИКЕ
ОТЧЕТ
Тема:
ИЗМЕРЕНИЕ ПАРАМЕТРОВ ЁМКОСТЕЙ
Цель работы: Определение импеданса, сдвига фаз и измерение емкости на разных частотах в резистивно-емкостной цепи.
Переменный ток – это электрический ток, изменяющийся во времени. В общем понимании к переменному току относят различные виды импульсных, пульсирующих, периодических и квазипериодических токов. В технике под переменным током обычно подразумевают периодические или почти периодические токи переменного направления. Наиболее употребителен переменный ток, сила которого меняется во времени по гармоническому закону.
Если к активному сопротивлению R приложено переменное напряжение U = Umcos(t), то текущий ток через это сопротивление по закону Ома будет равен
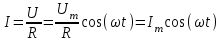
Если переменное напряжение, изменяющееся по гармоническому закону, подано на конденсатор C, то в этой элементарной цепи конденсатор непрерывно перезаряжается (в цепи будет течь переменный ток), и при отсутствии падения напряжения в проводах напряжение на конденсаторе равно внешнему напряжению:
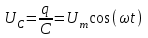
Так как I = dq/dt, то
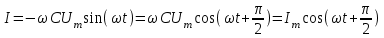,Величина XC называется ёмкостным сопротивлением. Следовательно, через конденсатор может течь переменный ток тем больший, чем больше частота тока и емкость С. Для постоянного тока, т.е. у которого = 0, ёмкостное сопротивление становится бесконечно большим: постоянный ток не может течь через конденсатор.
Поскольку рассматриваемые резистор и конденсатор соединены последовательно, эти токи равны между собой и равны общему току I, потребляемому схемой. Из данной диаграммы видно, что угол сдвига фаз
теор можно найти так:
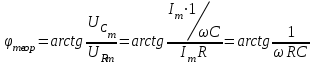,Таким образом, измеряя амплитуды входного напряжения и напряжения на резисторе с учетом формул и учитывая, что действующие и амплитудные напряжения отличаются в одно и то же число (в
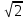раз), можно получить выражение для величины измеряемой ёмкости: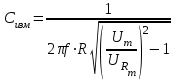
Схема установки:
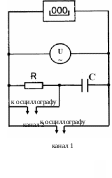
Результаты измерений
Таблица 1 – измерение напряжений и ёмкости в RC - цепи.
| f, кГц | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| Um, B | 3 | |||||||||
| URm, B | 1,1 | 1,7 | 2,2 | 2,4 | 2,6 | 2,7 | 2,7 | 2,7 | 2,8 | 2,8 |
| Cизм, мкФ | 4,2 | 3,6 | 3,8 | 3,5 | 3,7 | 3,7 | 3,1 | 2,7 | 3,1 | 2,8 |
| Z, Ом | 409,1 | 264,7 | 204,5 | 187,5 | 173,1 | 166,7 | 166,7 | 166,7 | 160,7 | 160,7 |
Таблица 2 – Измерение фазового сдвига в RC - цепи.
| f, кГц | 0,05 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1 |
| t, мс | 4 | 1,9 | 0,6 | 0,3 | 0,2 | 0,15 | 0,1 | 0,09 | 0,06 | 0,05 | 0.03 |
| T, мс | 20 | 10 | 5 | 3,33 | 2,5 | 2 | 1,67 | 1,4 | 1,25 | 1,1 | 1 |
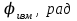 | 1,257 | 1,194 | 0,754 | 0,566 | 0,503 | 0,471 | 0,376 | 0,404 | 0,302 | 0,286 | 0,251 |
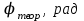 | | 1,195 | 0,968 | 0,748 | 0,644 | 0,522 | 0,451 | 0,451 | 0,451 | 0,367 | 0,367 |
Формулы погрешностей прямых и косвенных измерений, примеры
расчётов:
; 
; 
; 
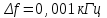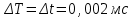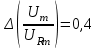
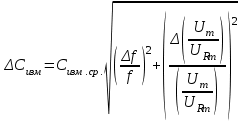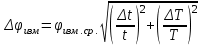
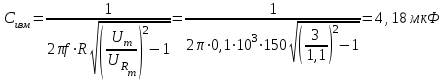
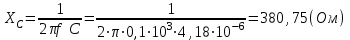
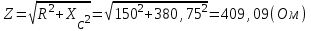
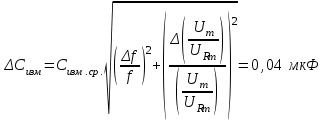
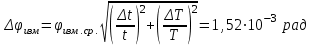
Графики зависимостей:
1) График зависимости импеданса цепи от частоты Z=Z(f):
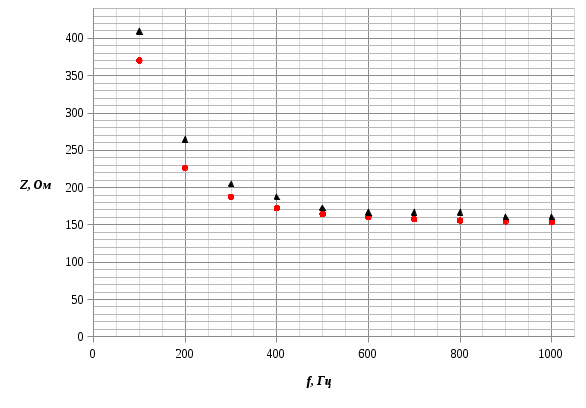
2) Графики фазочастотных характеристик:
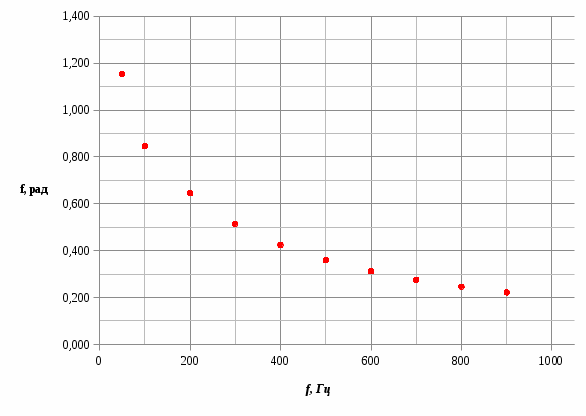
3) График амперочастотной характеристики, Im= Im(f):
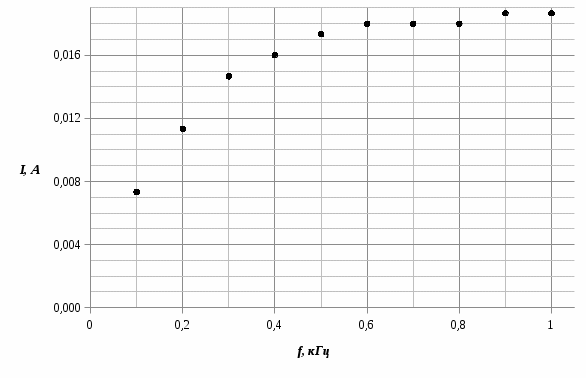
Итоговый результат:
; 
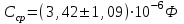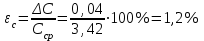.Вывод: В ходе выполнения лабораторной работы была вычислена емкость конденсатора
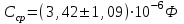. По полученным значениям были построены графики зависимости полного сопротивления цепи, фазового сдвига, силы тока в цепи от частоты и построены графики, иллюстрирующие данную зависимость.