Файл: санктпетербургский горный университе т.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 30

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Кафедра общей и технической физики
Лаборатория механики

Отчет по лабораторной работе №7



По дисциплине:
                                       Физика







Тема:
Определение момента инерции твёрдых тел с помощью маятника Максвелла



Автор:

студент гр.
ГГ-22-1









Агафонов Р. Ю.












(подпись)



(Ф.И.О.)

Оценка: ____________

Дата: ________

Проверил:


















(должность)



(подпись)



(Ф.И.О.)

Санкт-Петербург

2023

Цель работы – изучить устройство маятника Максвелла и определить с его помощью момент инерции твёрдых тел.

Краткое теоретическое содержание

Явление, изучаемое в работе: инертность тела при вращательном движении
Вращательное движение — это движение объекта вокруг оси или центра вращения. При вращательном движении материальная точка описывает окружность.


Поступательное движение — механическое движение системы точек (абсолютно твёрдого тела), при котором отрезок, связывающий любые две точки этого тела, форма и размеры которого во время движения не меняются, остаётся параллельным своему положению в любой предыдущий момент времени.

Момент инерции тела – мера инертности тела при вращательном движении, которая зависит от размеров и формы тел и от распределения массы тела относительно оси вращения.

Законы и соотношения, использованные при выводе расчетных формул



Момент инерции дискретного тела на основе свойства аддитивности момента инерции:



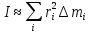
Момент инерции сплошного твёрдого тела (непрерывное распределение масс):



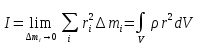
В нижнем положении маятника при 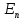= 0 полная механическая энергия равна сумме кинетических энергий поступательного 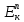и вращательного 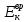движений: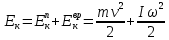



Связь угловой и линейной скоростей:



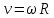
Уравнение для расстояния в равномерном движении:


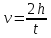
Схема установки



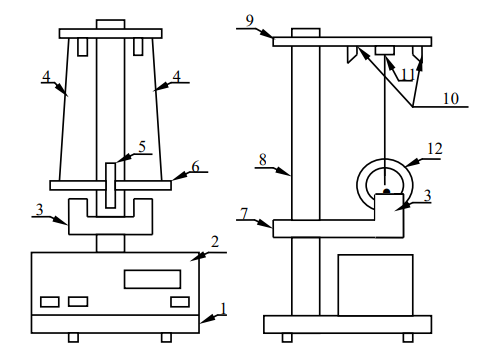
Где 1 – основание; 2 – секундомер; 3 – фотоэлектрический диэлектрик; 4 – нити (бифилярный подвес); 5 – диск; 6 – ось; 7 – подвижный кронштейн; 8 – колонка; 9 неподвижный кронштейн; 10 – электромагнит; 11 – фотоэлектрический датчик; 12 – сменное кольцо.

Основные расчетные формулы





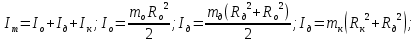
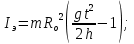
Где 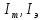– теоретическое и экспериментальное значения момента инерции маятника соответственно [кг*м2];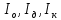
– моменты инерции оси маятника, диска и кольца, одетого на диск, соответственно [кг*м2]; 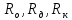– радиусы оси маятника, диска и кольца, одетого на диск, соответственно [м]; 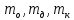– массы оси маятника, диска и кольца, одетого на диск, соответственно [кг]; 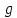– ускорение свободного падения [м/с2]; t – время [с]; h – высотка фиксации маятника [м];

Исходные данные





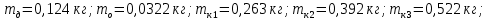
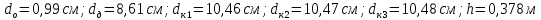
Относительная погрешность прямых измерений



Таблицы

Таблица измерений №1
Кольцо №1
Кольцо №2
Кольцо №3

Физическая величина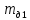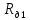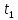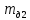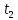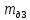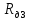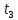


















Един. измерения
Номер опыта
кг
м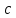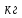




м
с
кг
м
с

1
0,263
0,0523
1,924
0,392
0,05235
1,986
0,522
0,0524
2,044

2






1,923






1,989






2,019

3






2,010






1,999






2,015

4






1,928






2,001






2,012

5






1,962






1,957






2,045

6






1,967






1,999






2,037

7






1,963






1,997






2,004

8






1,932






2,003






2,062

9






1,893






1,992






2,023

10






1,925






1,999






2,033

Формулы для расчета погрешности измерений



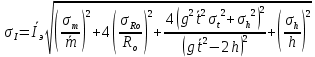
Где



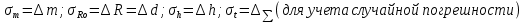
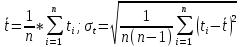
Квадратичная погрешность будет высчитываться отдельно для каждого диска, т.е. 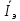– полученное экспериментальное значения для каждого диска, а 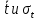– среднее время и квадратичная погрешность времени для каждого диска соответственно.

Квадратичная погрешность













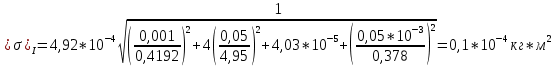
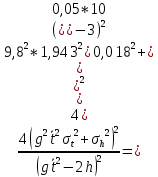
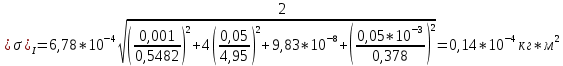
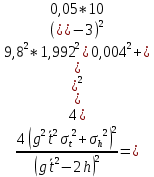
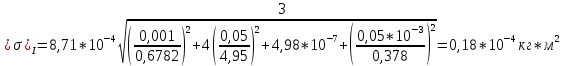
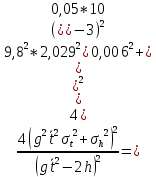
Относительная погрешность







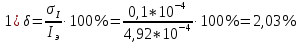
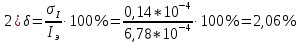
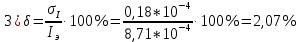
Примеры вычислений

(Для кольца №1)













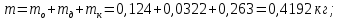
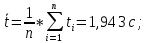
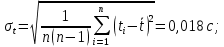
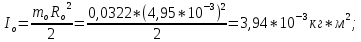
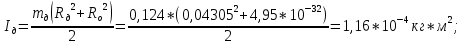
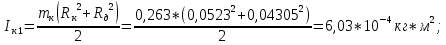
Моменты инерции системы тел:

Кольцо №1





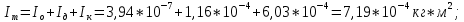
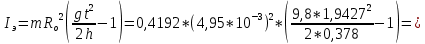
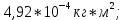
Кольцо №2





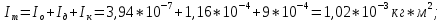
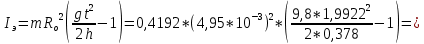
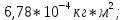
Кольцо №3












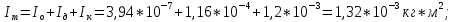
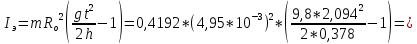
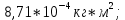
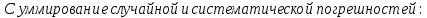
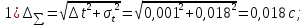
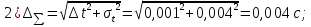
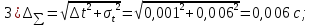
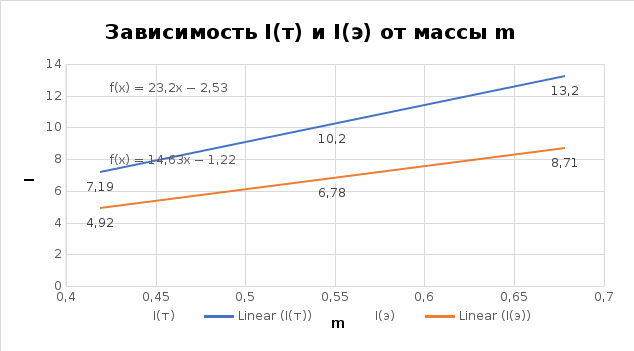
Графический материал

кг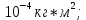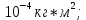




m
I(т)
I(э)

0.4192
7.19
4.92

0.5482
10.2
6.78

0.6782
13.2
8.71



Окончательный результат






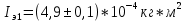
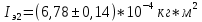
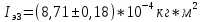
Вывод

В ходе этой лабораторной работы я изучил устройство маятника Максвелла и определил с его помощью момент инерции твёрдых тел, полученные экспериментальные значения моментов инерции для системы тел в трёх различных опытах равны 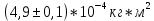; 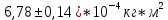и 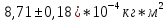соответственно.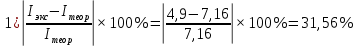






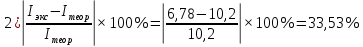
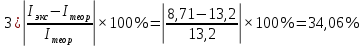
Показатели экспериментального значения момента инерции меньше теоретического приблизительно на 31-34%.

Смотрите также файлы