Файл: Задача а задача в задача с задача 2а задача 2б задача А.docx
Добавлен: 23.11.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)»
(МАИ)
Кафедра «Технология испытаний и эксплуатации»
Отчёт по курсовой работе
по дисциплине «Прикладная механика» (4 семестр)
(Вариант 68)
Студент А. Е. Елисеенко
Группа Т12О – 201С – 19
Дата сдачи
Подпись
Проверил Б. И. Болотников
Дата
Подпись
МОСКВА 2021
Содержание
-
Задача А -
Задача В -
Задача С -
Задача 2А -
Задача 2Б
-
Задача А
Построение эпюр продольных усилий и изгибающих
моментов для плоских систем.
Задание: Для плоской системы, заданной вариантом задания, построить эпюры продольных усилий и изгибающих моментов.
Вариант №68
Дано:
Р₁=14 кН;
q₁=2
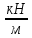 ;
; а=0,5 м;
Схема №9.
Задача А
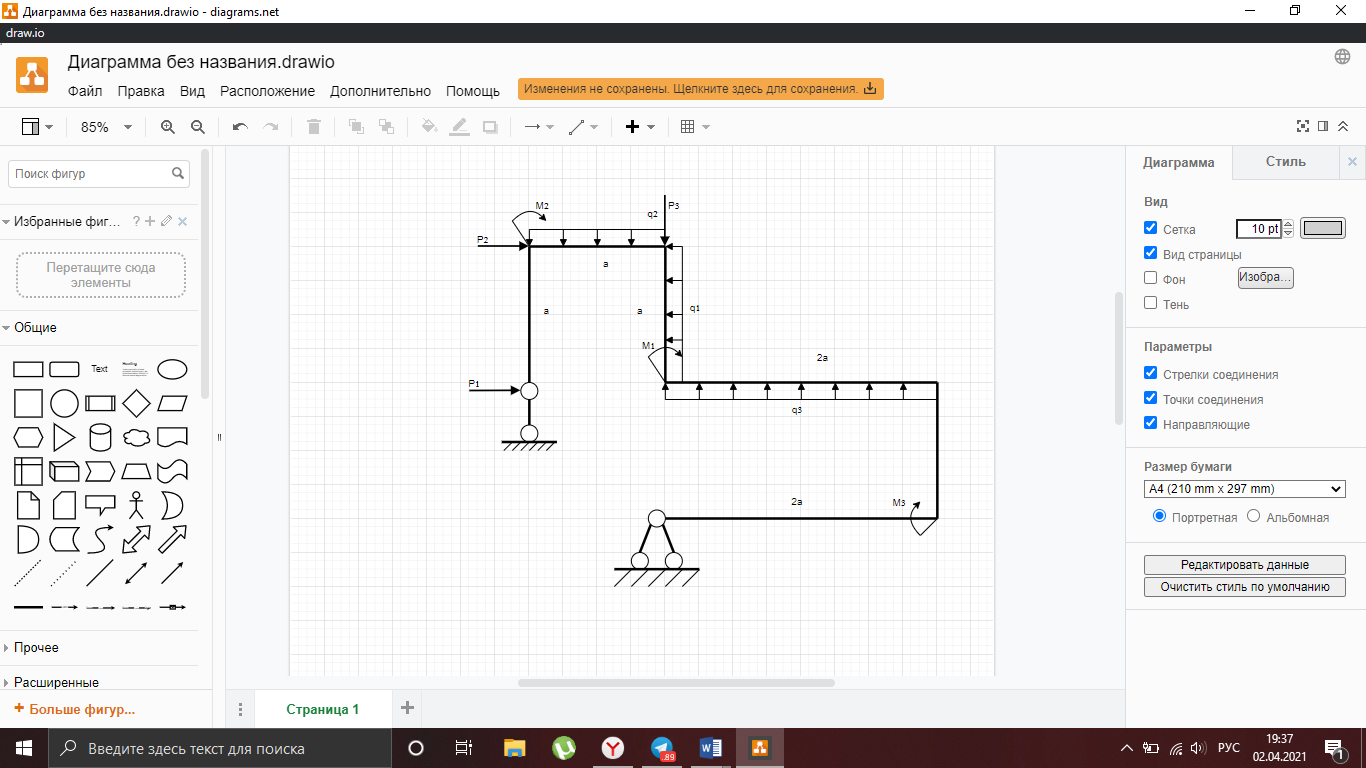
Рисунок 1 – Исходная схема
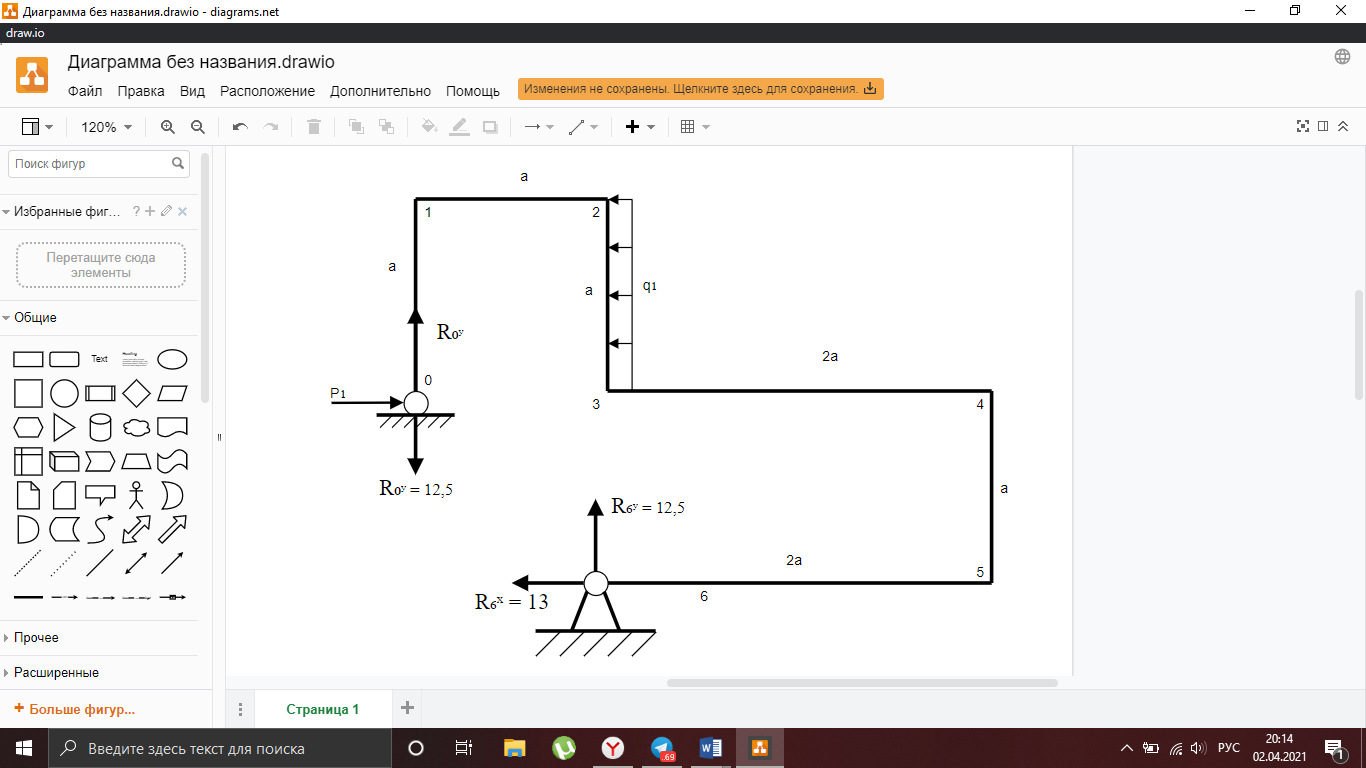
Рисунок 2 – Используемая схема
Расчёт
∑х=0
Р₁ - R₆ˣ - q₁ × a = 0
R₆ˣ = Р₁ - q₁ × a ⇒ 14 – 0,5 × 2 = 13
∑m₆ = 0
R₀ʸ×a + Р₁ × a -
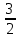 × q₁ × a²
× q₁ × a²R₀ʸ =
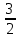
q₁ × a - P₁ ⇒
 × 2 × 0,5 – 14 = -12,5 кН
× 2 × 0,5 – 14 = -12,5 кН∑y = 0 ⇒ R₆ʸ = 12,5 кН
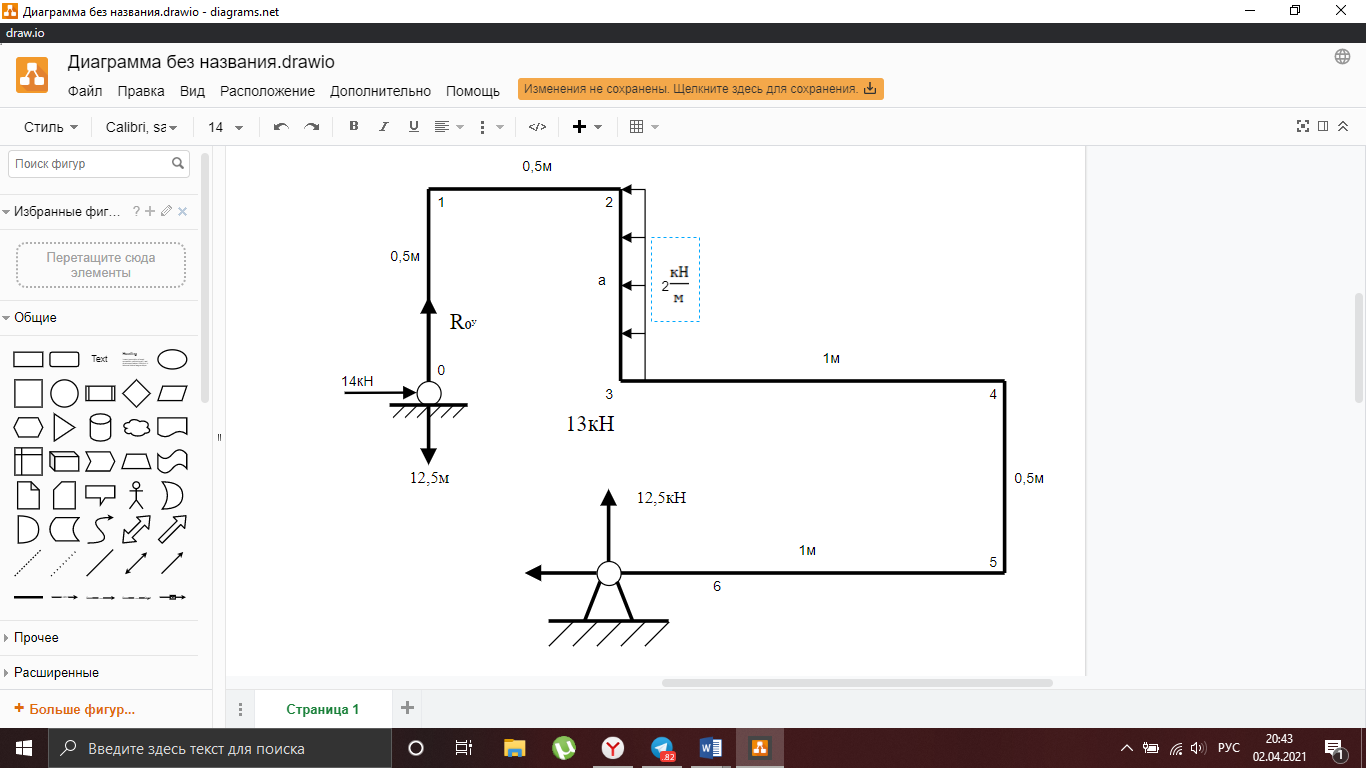
Рисунок 3
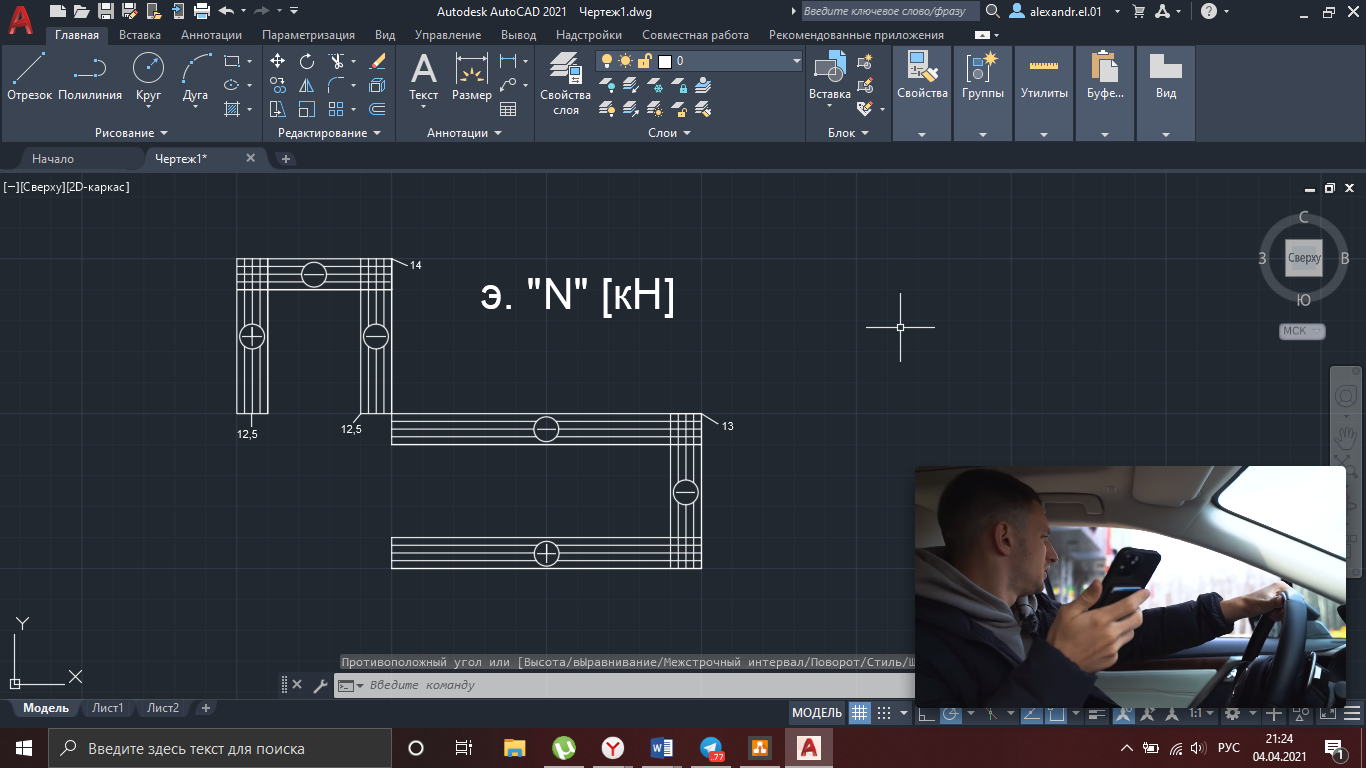
Рисунок 4
Рисунок 5
Мz₀₁ = -14x
Мz₁₂ = -7 – 12,5x
Мz₂₃ = -6,25 -
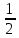 × 2x2 + 14(x – 0,5)
× 2x2 + 14(x – 0,5)Мz₃₄ = -12,5 (0,5 + x) – 0,25
Мz₄₅ = 14x – 18,75 - 1×(0,25 + x) + 14x
Мz₅₆ = - Мz₆₅
Мz₆₅ = 12,5x
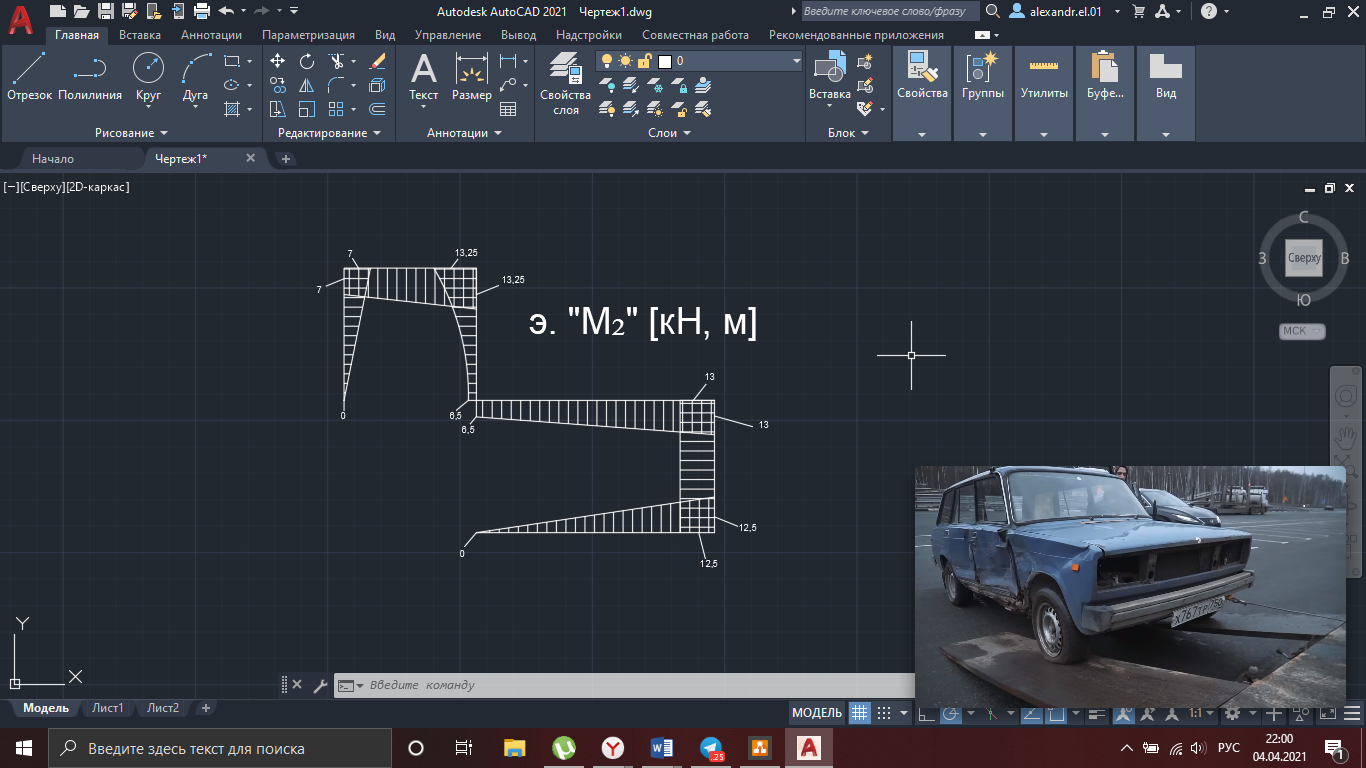
Рисунок 6
-
Задача В
Построение опор продольных усилий, крутящих
моментов и изгибающих моментов для пространственных систем.
Задание: Для пространственной системы, заданной вариантом задания, построить эпюры продольных, поперечных усилий, а также крутящих и изгибающих моментов.
Вариант №68
Дано:
Р₁=14 кН;
q₁=2
 ;
; а=0,5 м;
Схема №39.
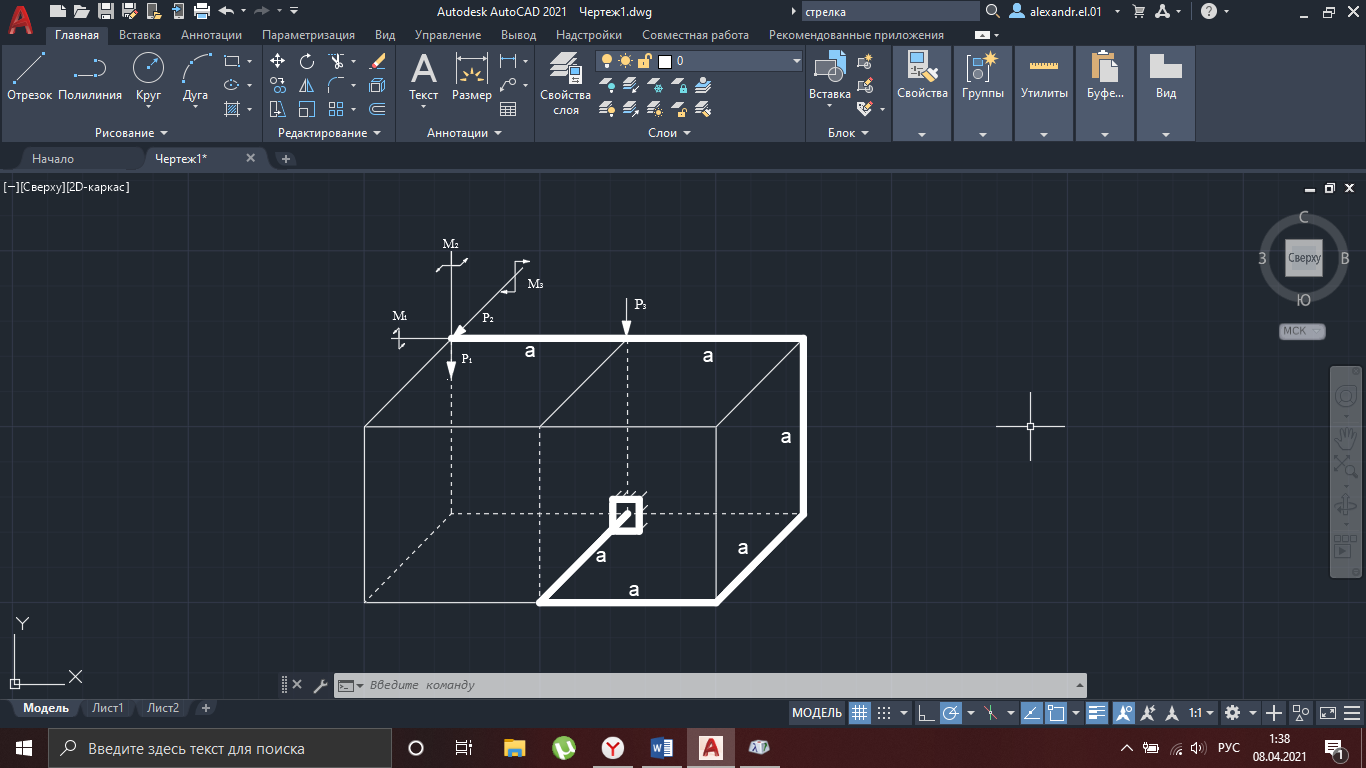
Рисунок 7 – Исходная схема
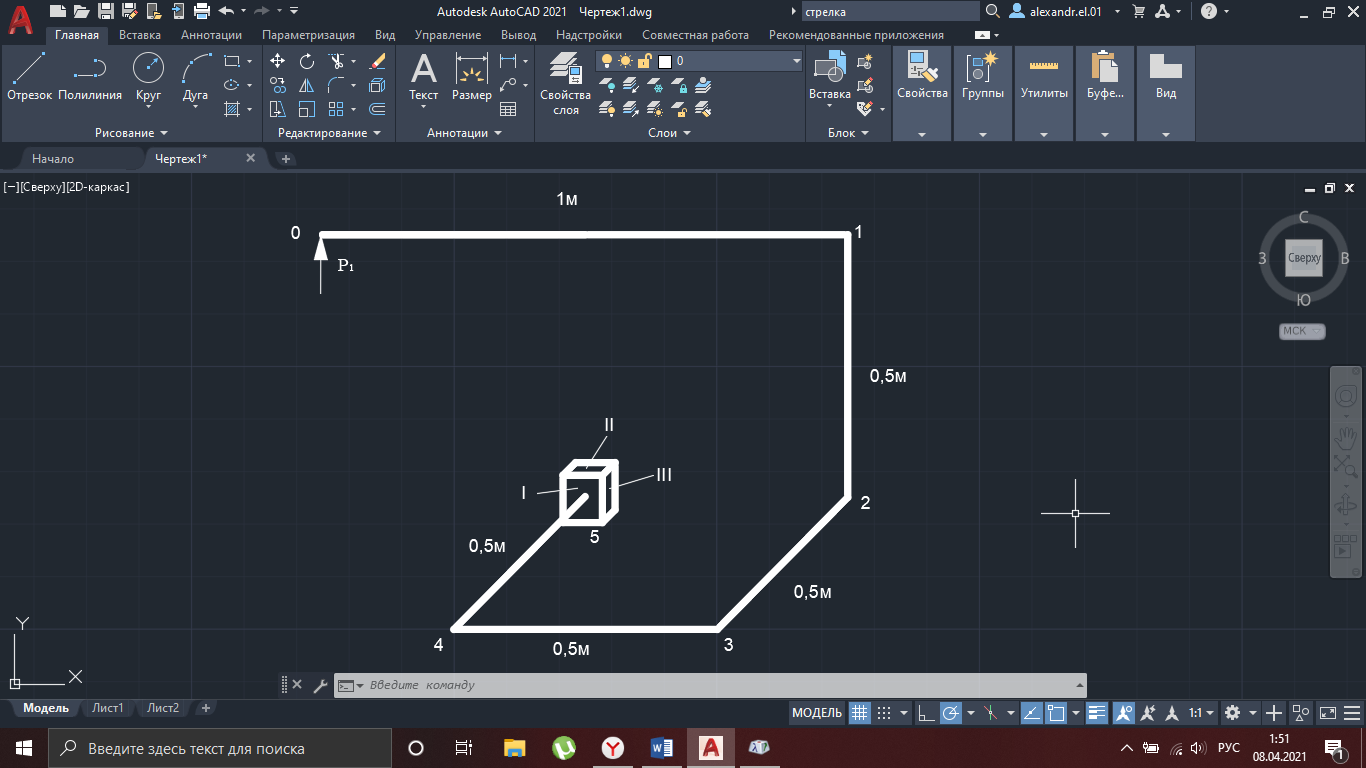
Рисунок 8 – Используемая схема
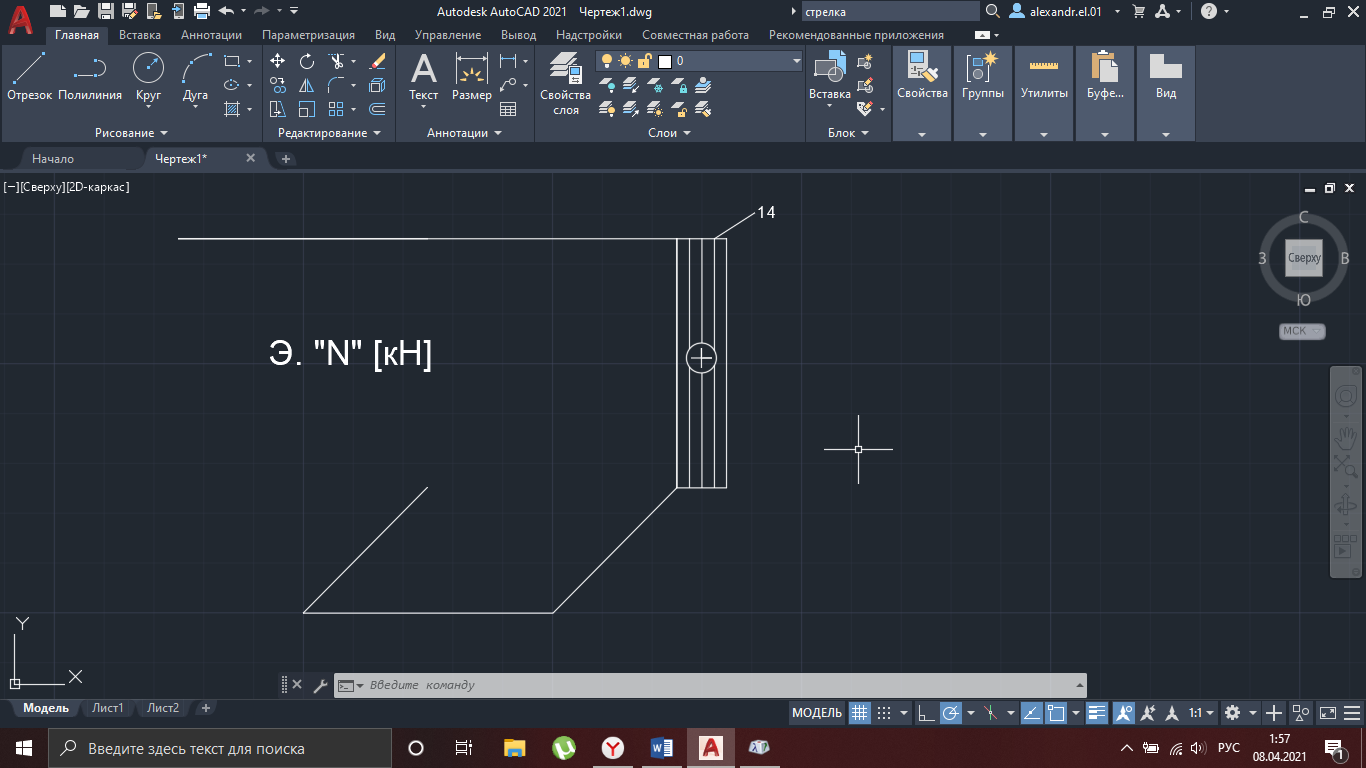
Рисунок 9
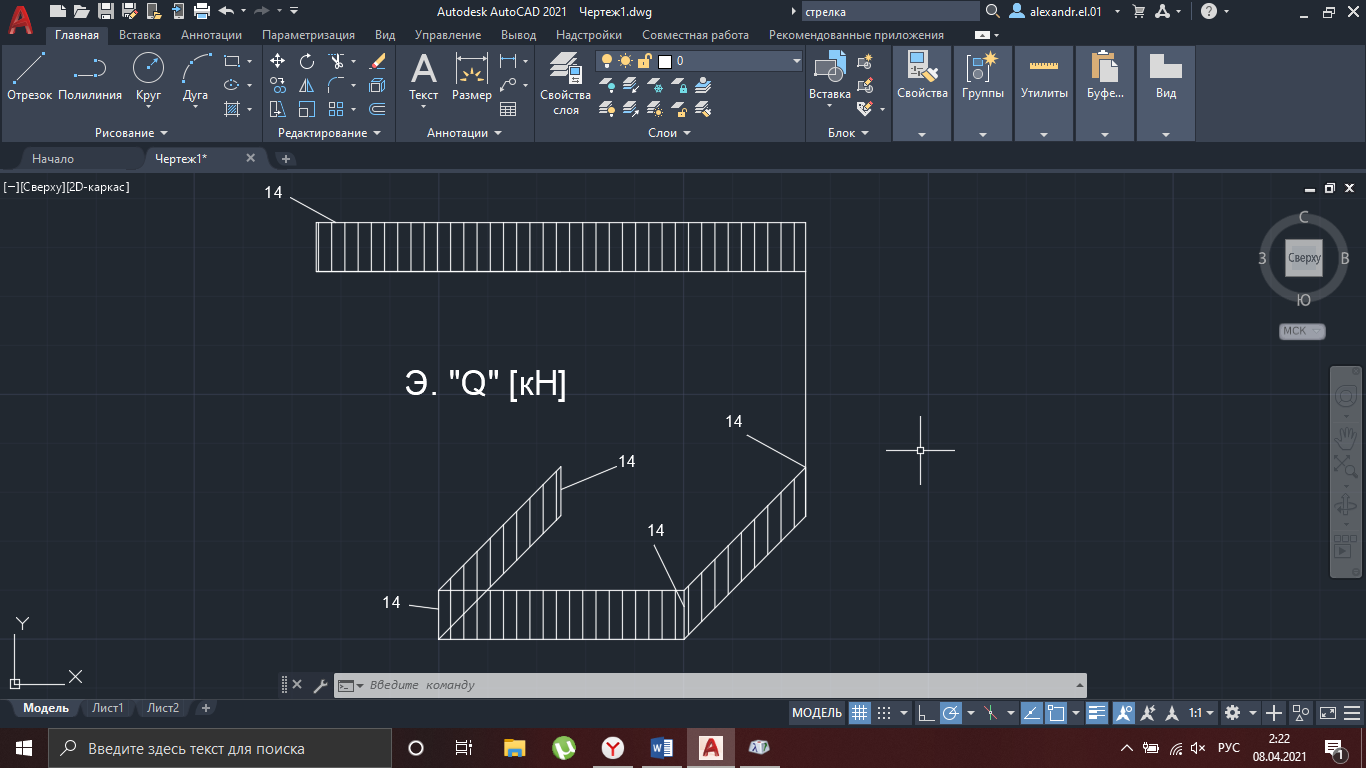
Рисунок 10
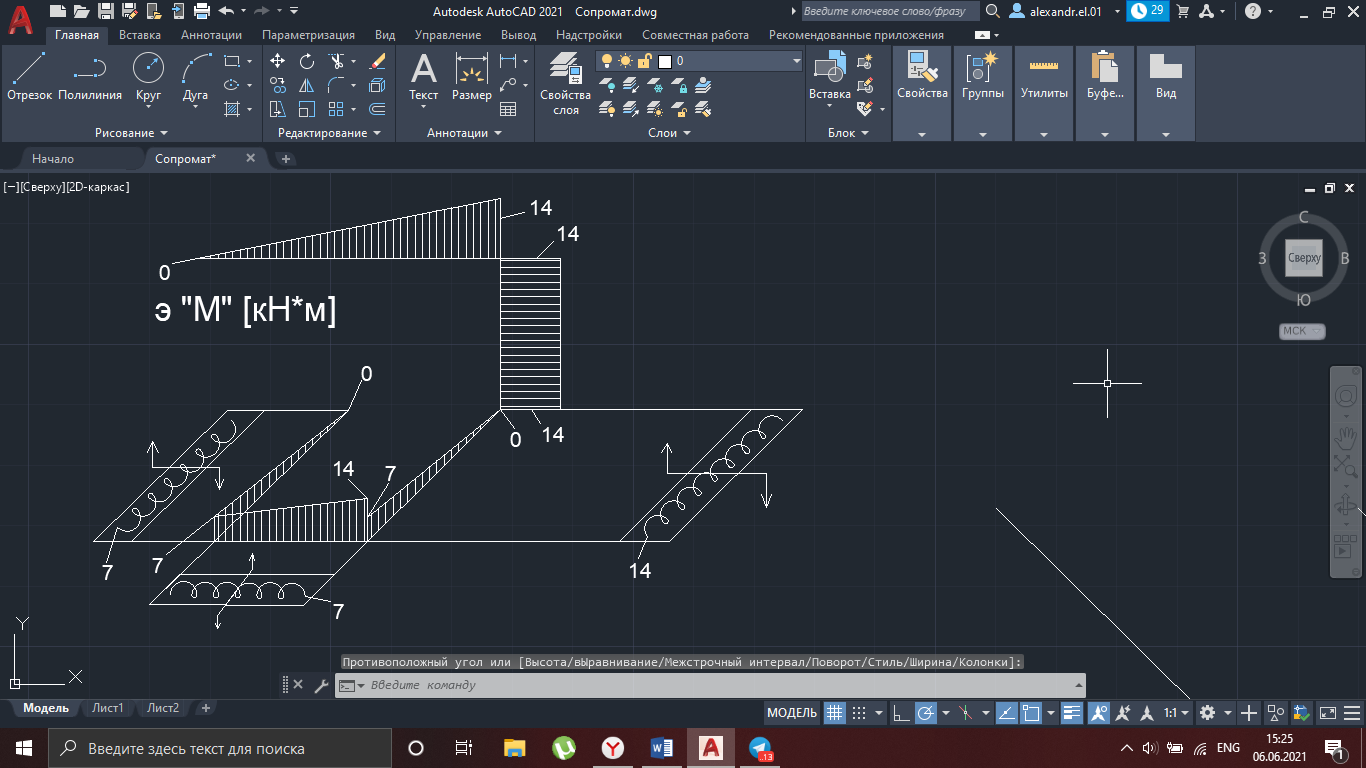
Рисунок 11
Расчёты:
у₂ 01
МzI = 14*x
у₂ 12
МzII = 14 кН*м
у₂ 23
МzIII = 14*x
МkI = 14 кН*м
у₂ 34
МzI = 14*(1-x)
МkII = 7 кН*м
у₂ 45
МzIII = 14*(0.5-x)
МkI = 7 кН*м
-
Задача С
Расчеты на прочность и жесткость при сложном
сопротивлении.
Задание: Для заданного ломаного бруса, имеющего круглые сечения в пределах элементов ????1 и ????2, прямоугольное сечение в пределах элемента длиной ????3, требуется выполнить расчеты.
Вариант №68
Дано:
l₁=25 см; b=3,5 см; [σ]=160МПа
l₂=23 см;
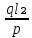 =1,1=>ql₂=1,1p
=1,1=>ql₂=1,1pl₃=30 см; h=2,5b
Схема №9.
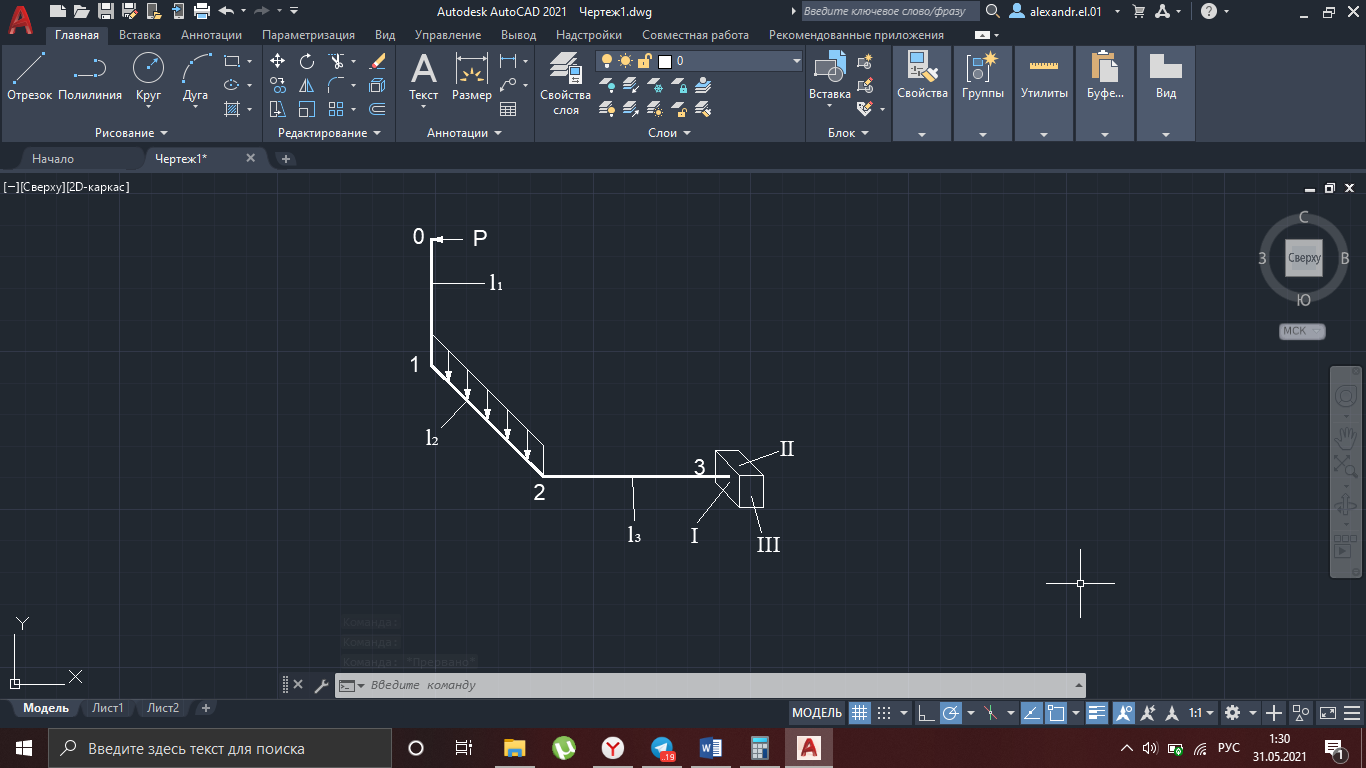
Рисунок 12 – Исходная схема
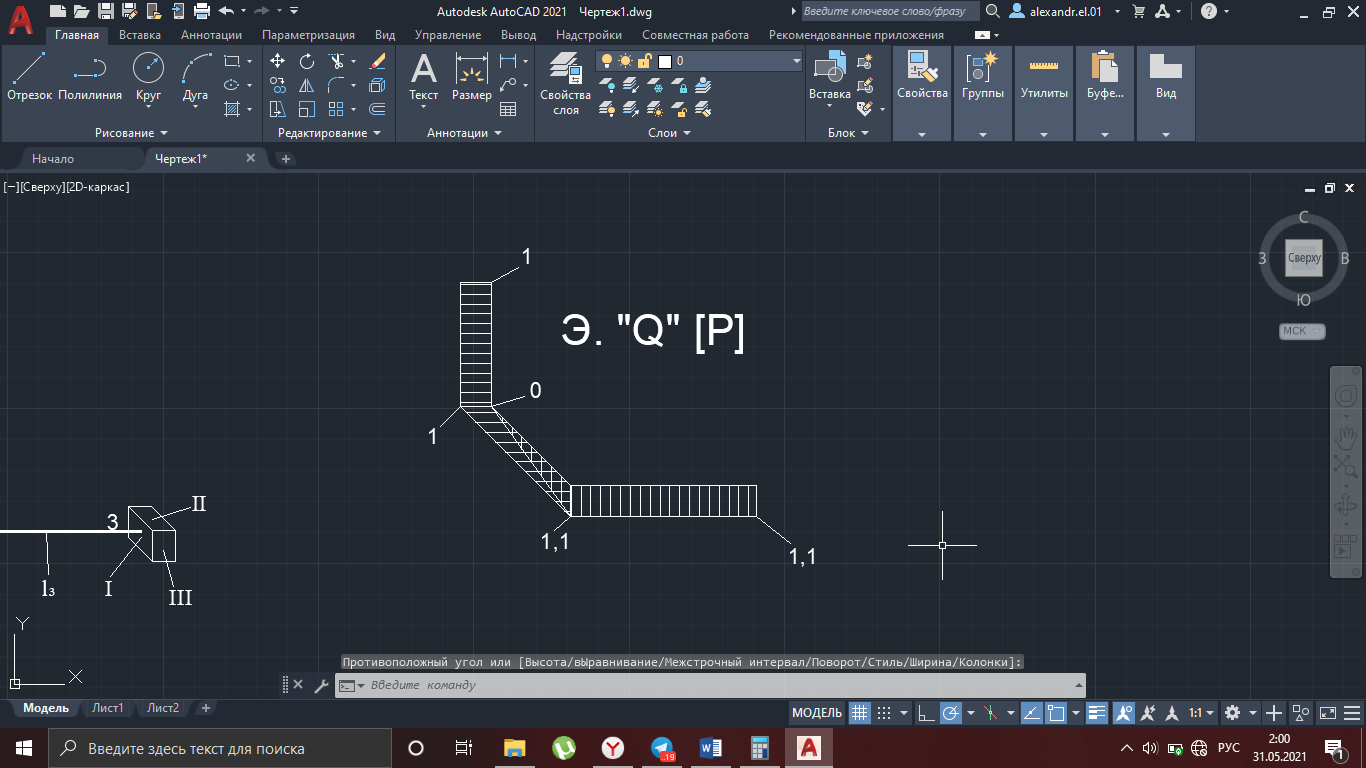
Рисунок 13 – эпюра «Q»
Расчёты:
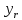 0’
0’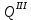 =P
=P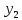 12
12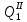 =P
=P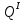 =qx
=qx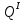 (0)=0;
(0)=0; 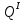 (l₂)=1,1P
(l₂)=1,1P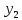 23
23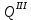 =1,1P
=1,1P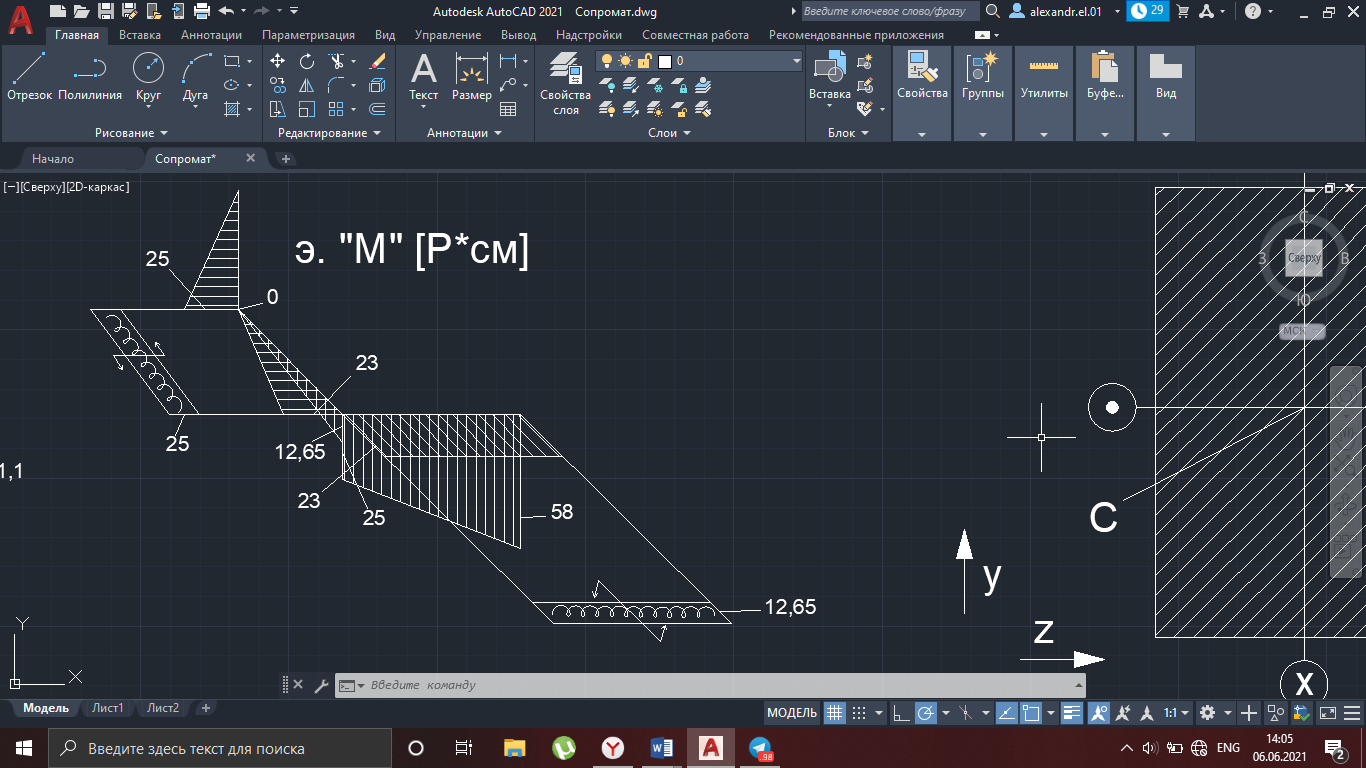
Рисунок 14 – эпюра «М»
Расчёты:
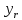 01 (l₁)
01 (l₁)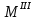 =
=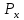
 12 (l₂)
12 (l₂)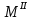 =
= ;
; 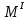 =
= q
q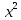
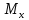 =25P
=25P 23 (l₃)
23 (l₃) =25P+1,1P*x
=25P+1,1P*x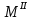 =23P
=23P2.
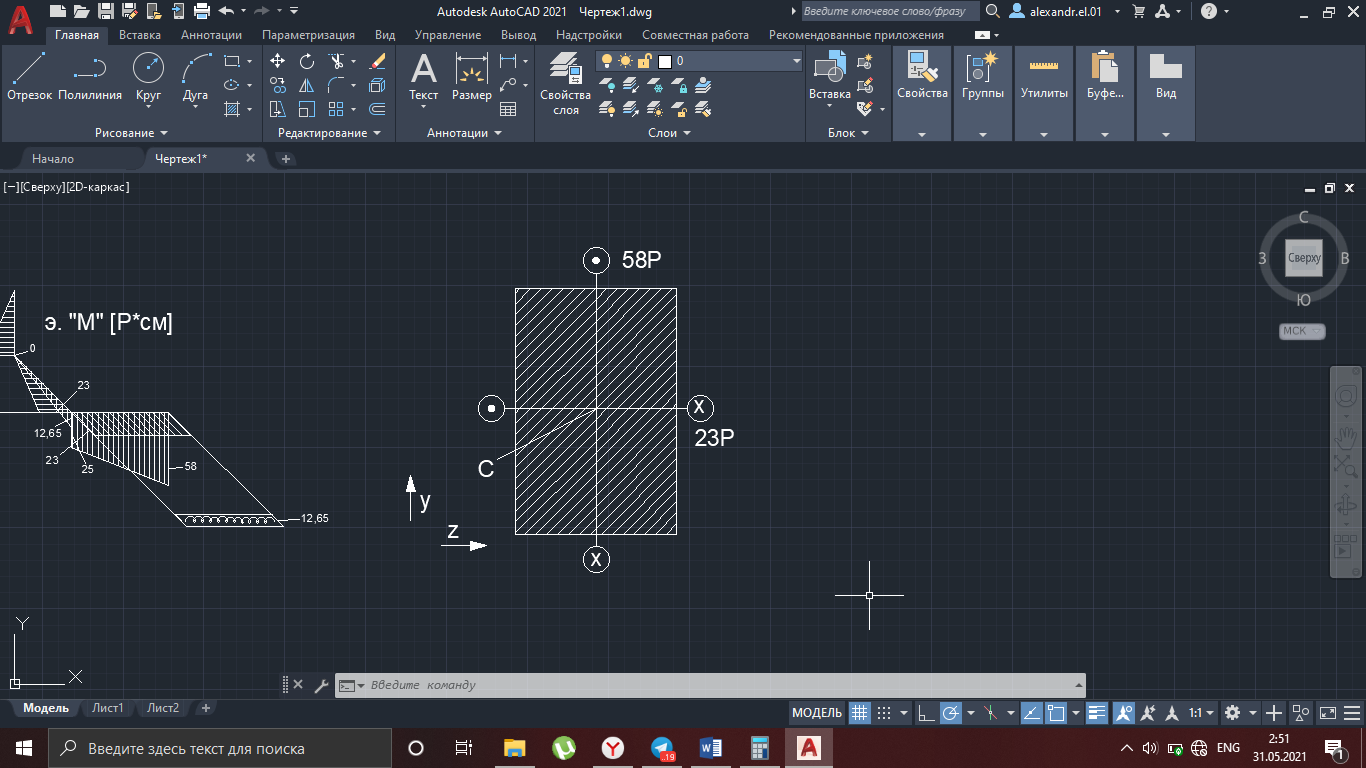
Рисунок 15
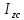 =
=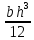
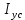 =
=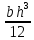
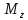 =58P
=58P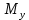 =23P
=23Pσ (y, z)=
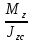 y +
y + 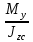 z
zс учетом знаков
σ (y, z)=
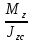 y -
y - 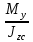 z
z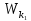 = αh2b;
= αh2b; 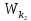 = αh
= αh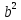
α=0,258 (
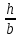 = 2,5)
= 2,5)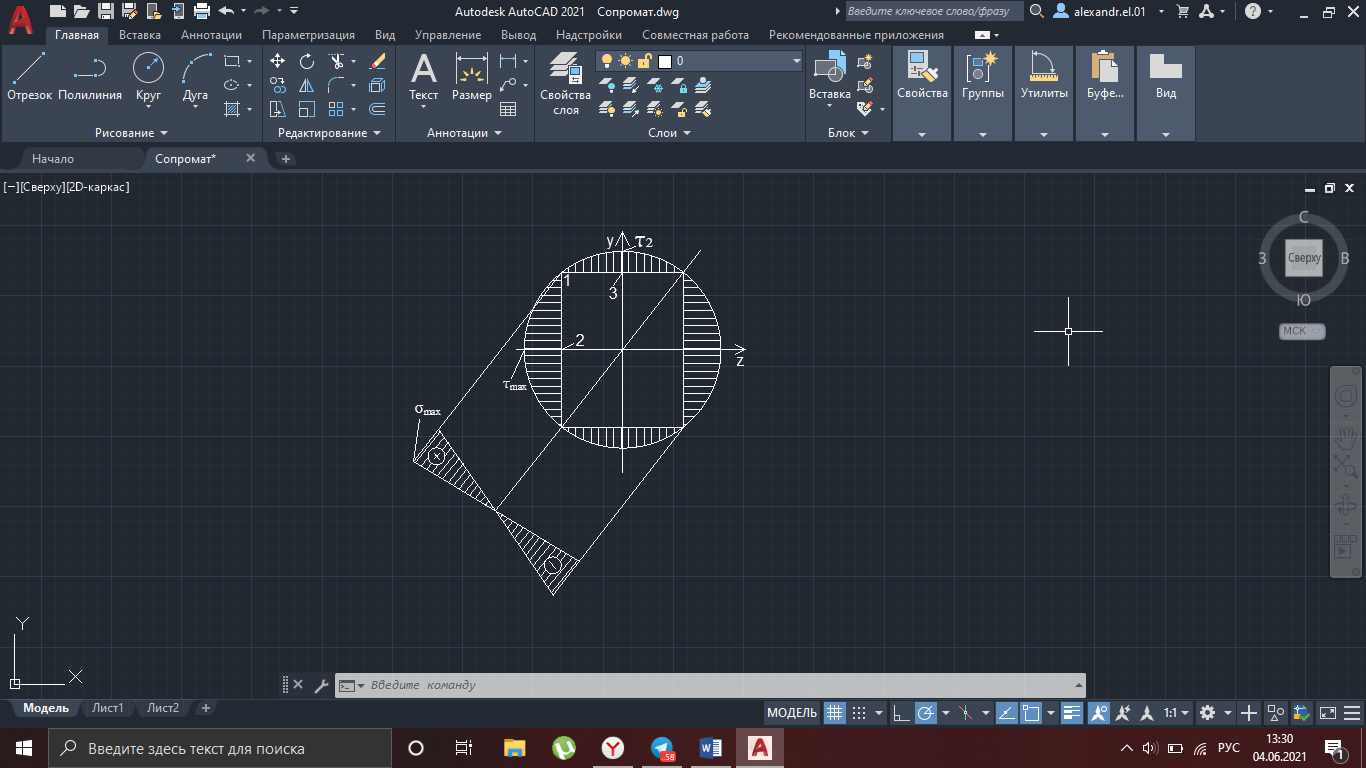
Рисунок 16
Определим нормальные напряжения в предполагаемых опасных точках.
1. (-
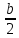 ;
; 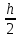 )
)
σ₁=
 *
*  +
+ 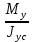 *
* 
σ₁=
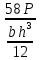 *
*  +
+ 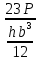 *
* 
σ₁= 2.169P + 4.416P = 6.585P.
2. (-
 ; 0)
; 0)σ₂= 4.416P
3. (0;
 )
)σ₃= 2.169P
Рассчитаем касательное напряжение в крит.точках:
τ₁= 0;
τ₂=
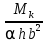 =
= 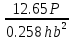 = 0.951P
= 0.951Pτ₃ =
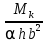 = 0.288P
= 0.288PТ.3 не является критической, т.к. σ₂> σ₃; τ₂>τ₃.
 Выберем из точек 1 и 2 самую опасную
Выберем из точек 1 и 2 самую опасную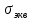 =
= 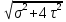 ≤ [σ] – условие прочности
≤ [σ] – условие прочности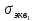 =
= 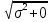 = σ = 6.585Р
= σ = 6.585Р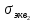 =
= 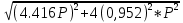 = 4.81Р =>
= 4.81Р =>=>т.1 – наиболее опасная, т.о.
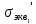 ≤ [σ]
≤ [σ]6.585P ≤ [σ