Файл: Задача а задача в задача с задача 2а задача 2б задача А.docx
Добавлен: 23.11.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
] => P ≤ 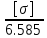 =
= 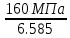 = 2429.7H
= 2429.7H
ql₂ = 1.1P
q =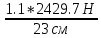 = 116.2
= 116.2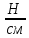
3.
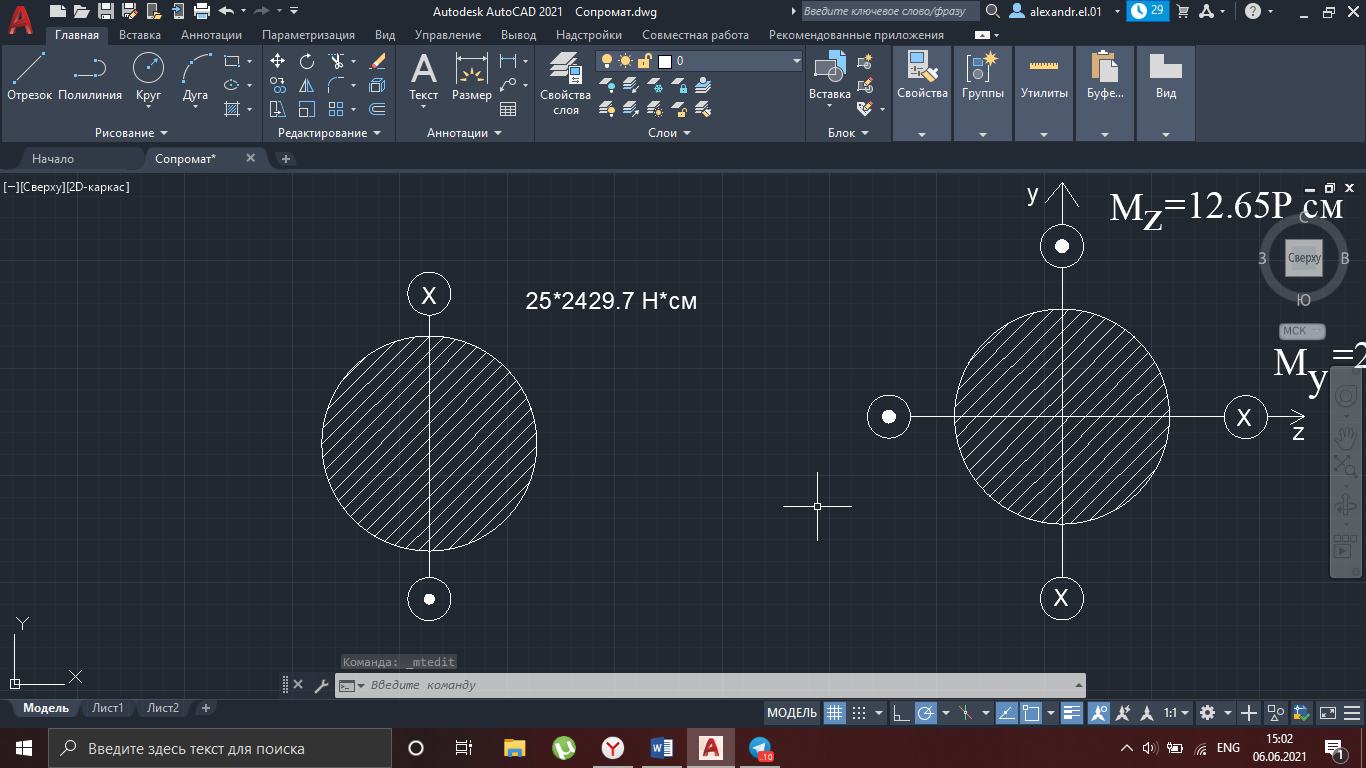
Рисунок 17
Уч. 01
Условие прочности
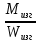 ≤ [σ]
≤ [σ]
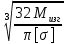 ≤ d
≤ d
d ≥ 5.317 см
Уч. 12
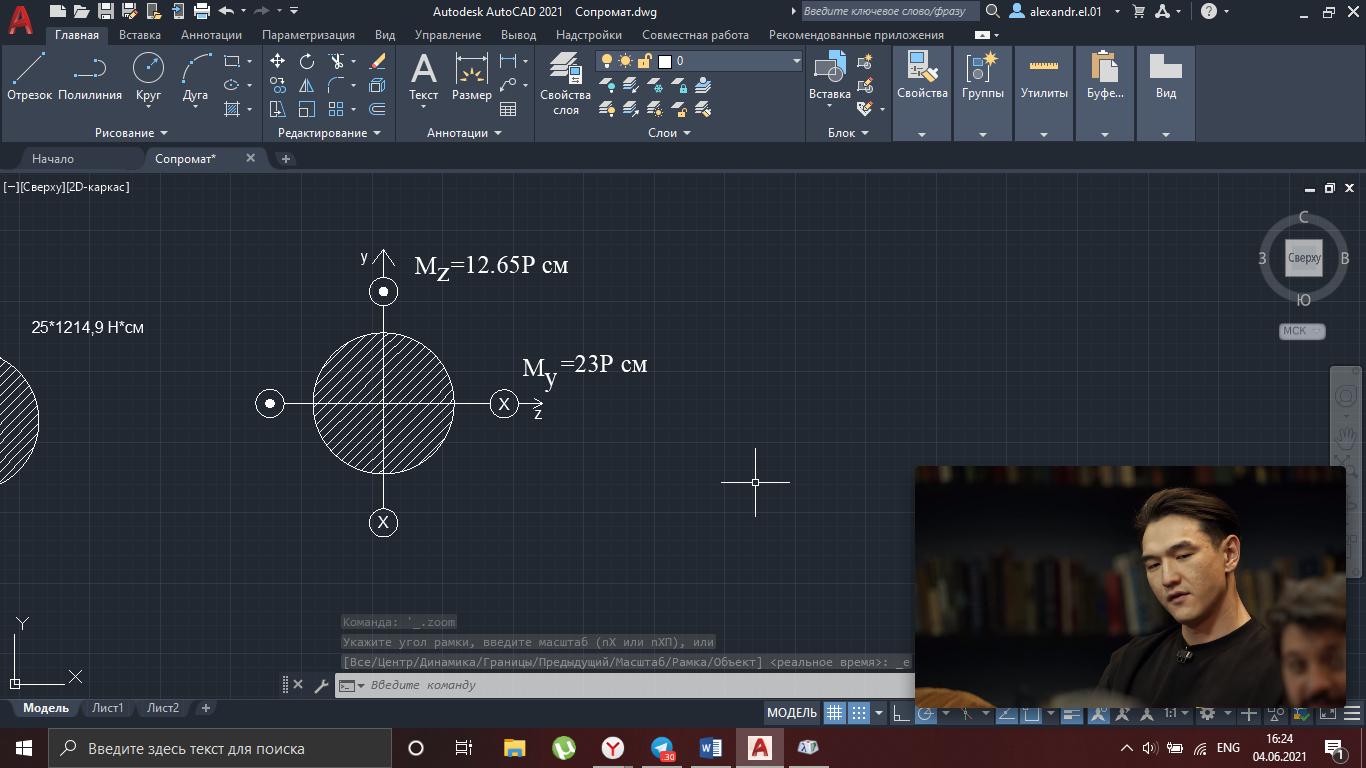
Рисунок 18
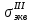 =
=  ≤ [σ]
≤ [σ]
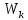 ≈ 0.2d3
≈ 0.2d3
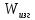 ≈ 0,1d3
≈ 0,1d3
σ =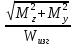
τ =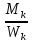
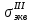 =
= 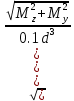 ≤ [σ]
≤ [σ]
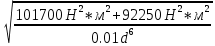 ≤ [σ]
≤ [σ]
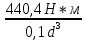 ≤ [σ] => d ≥
≤ [σ] => d ≥ 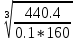 = 6 см
= 6 см
Расчет статически неопределимых систем при изгибе.
Вариант №68
Дано:
q2 = 16
Р1 = 18кН
а = 1,1м
Схема №11
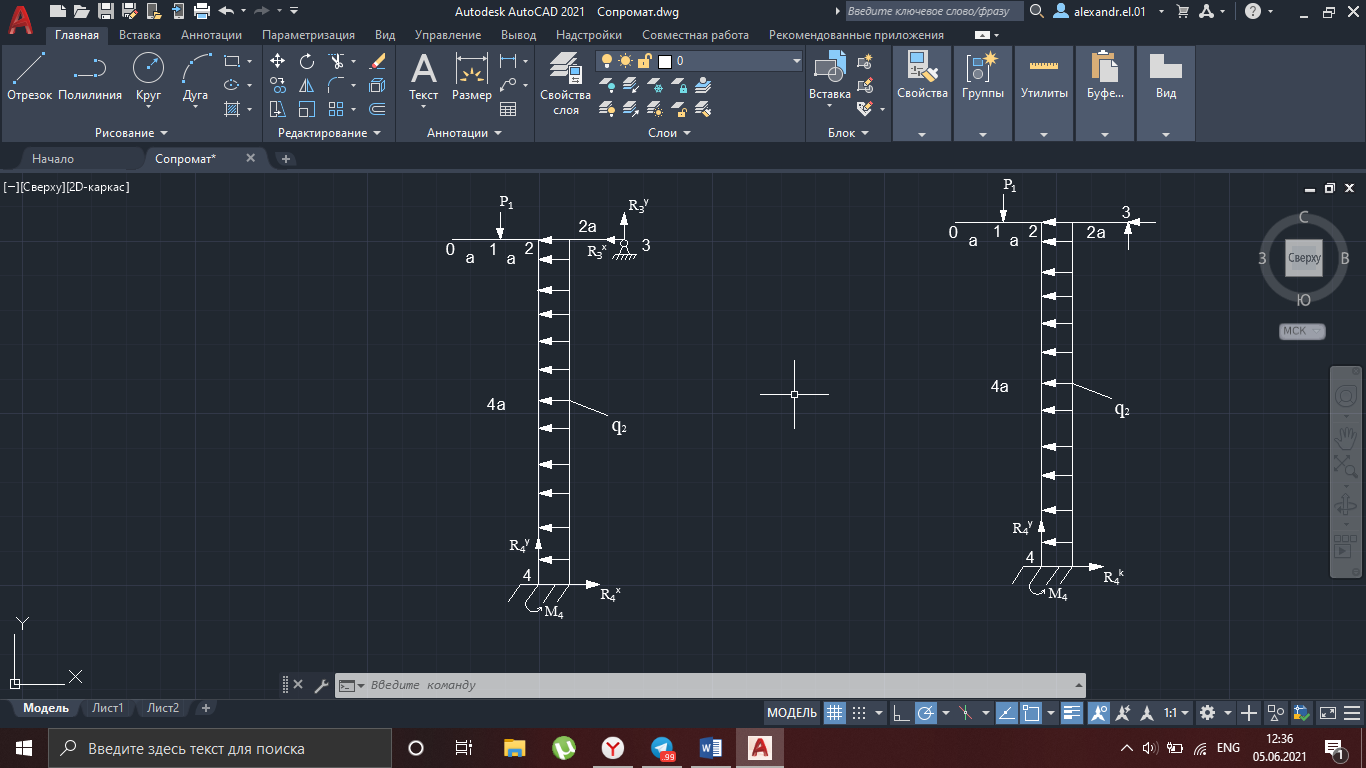
Рисунок 19 – Исходная схема
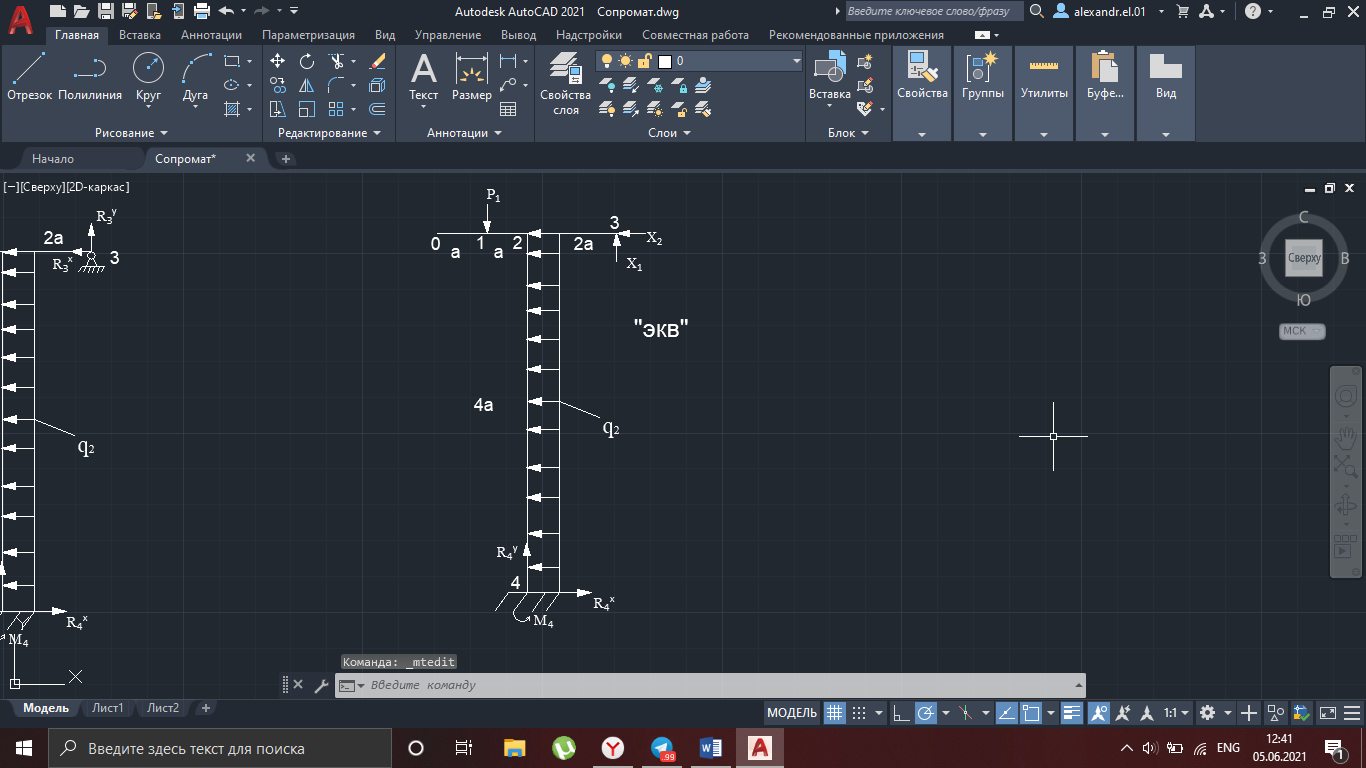
Рисунок 20
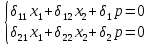
Построим грузовую эпюру:
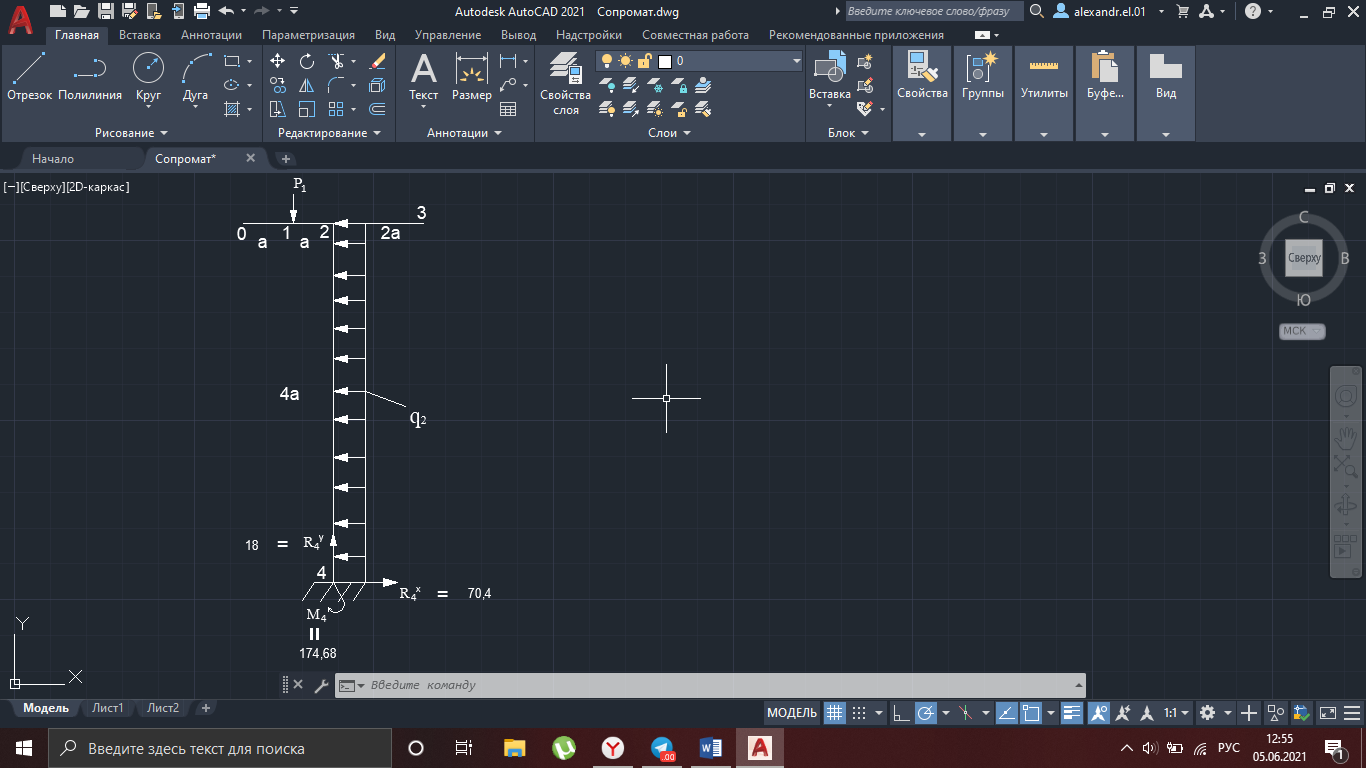
Рисунок 21
Расчёты:
∑x = 0:
R4x = 4*q2*a = 70.4кН
∑y = 0:
R4y = R1 = 18кН
∑М4 = 0:
М4 + 4*q2*a * 2a + P1*a = 0
M4 = -8*16*1.12 – 18*1.1 = -174.68 кН*м
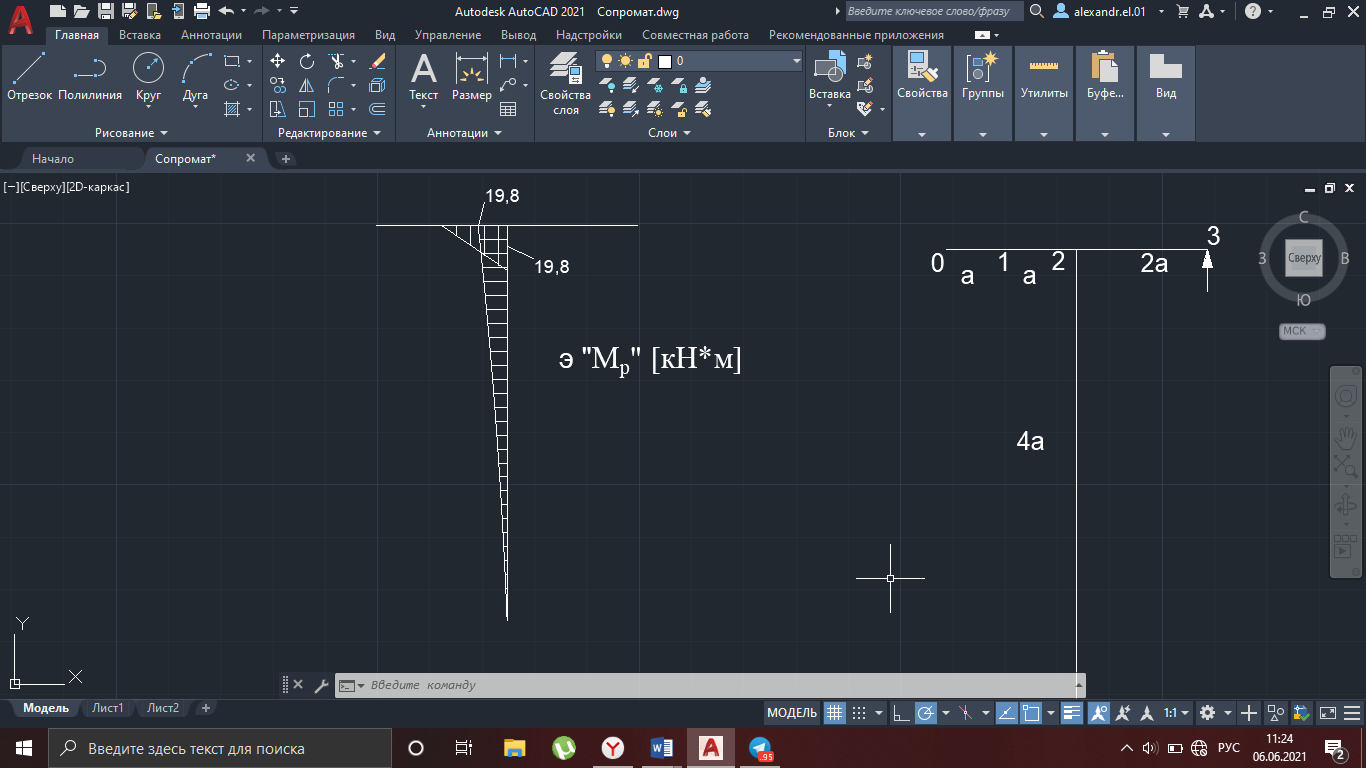
Рисунок 22
2.
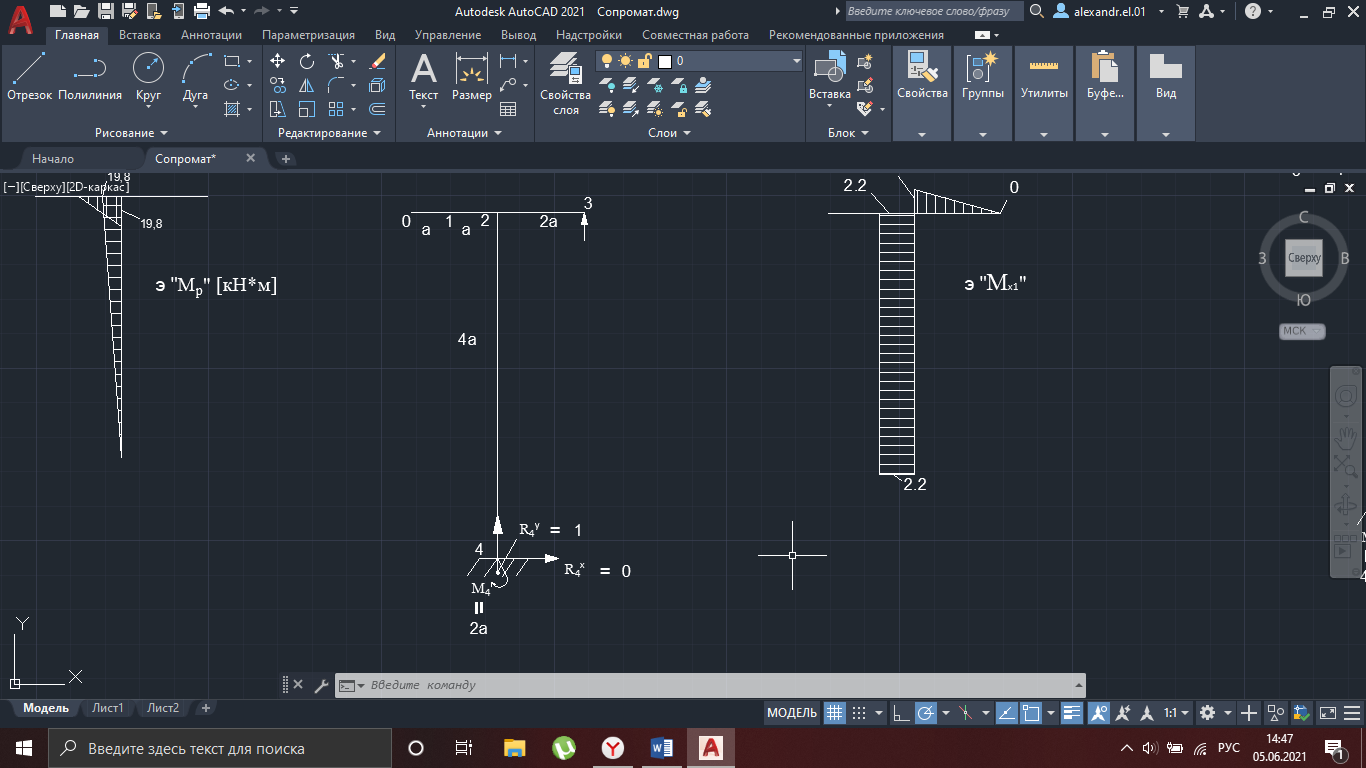
Рисунок 23
∑х = 0:
R4x = 0
∑y = 0:
R4y = -1
∑M4 = 0:
M4 + 2a = 0:
M4 = -2a
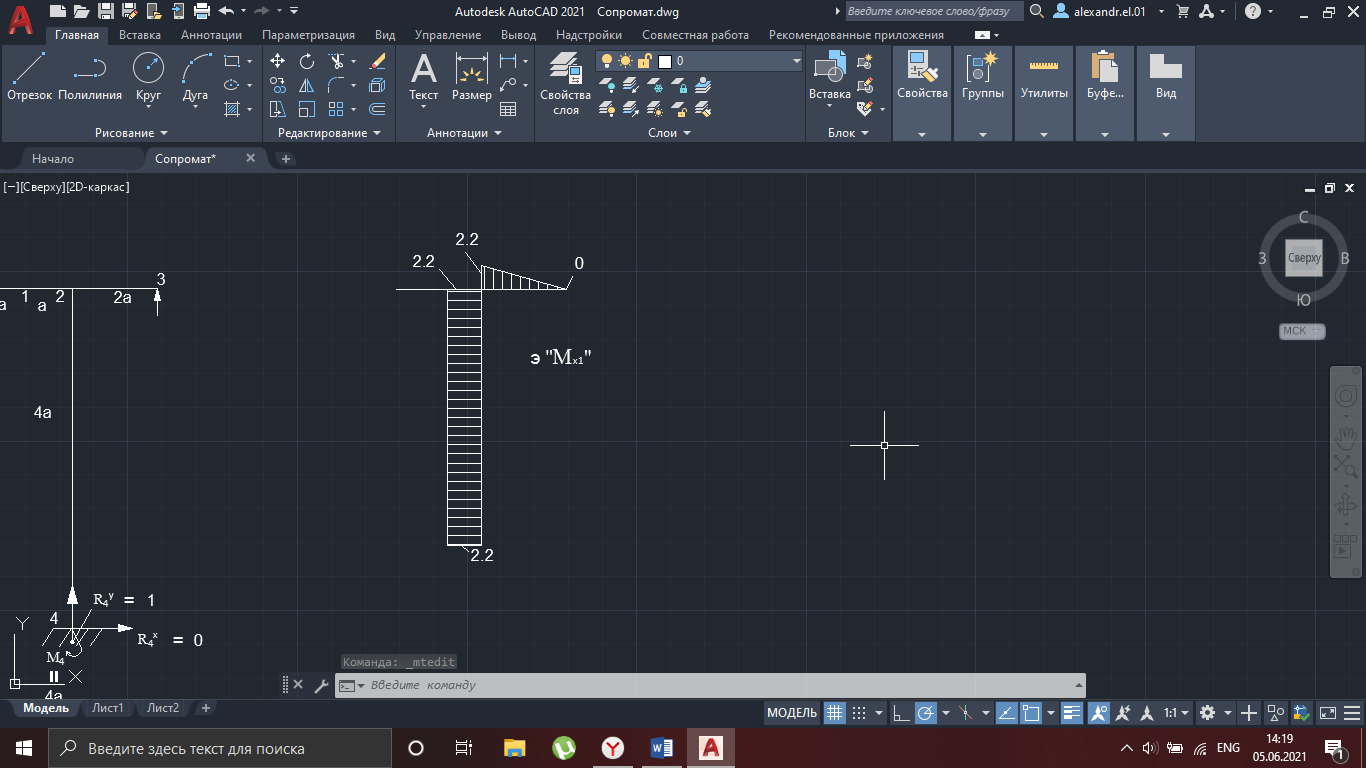
Рисунок 24
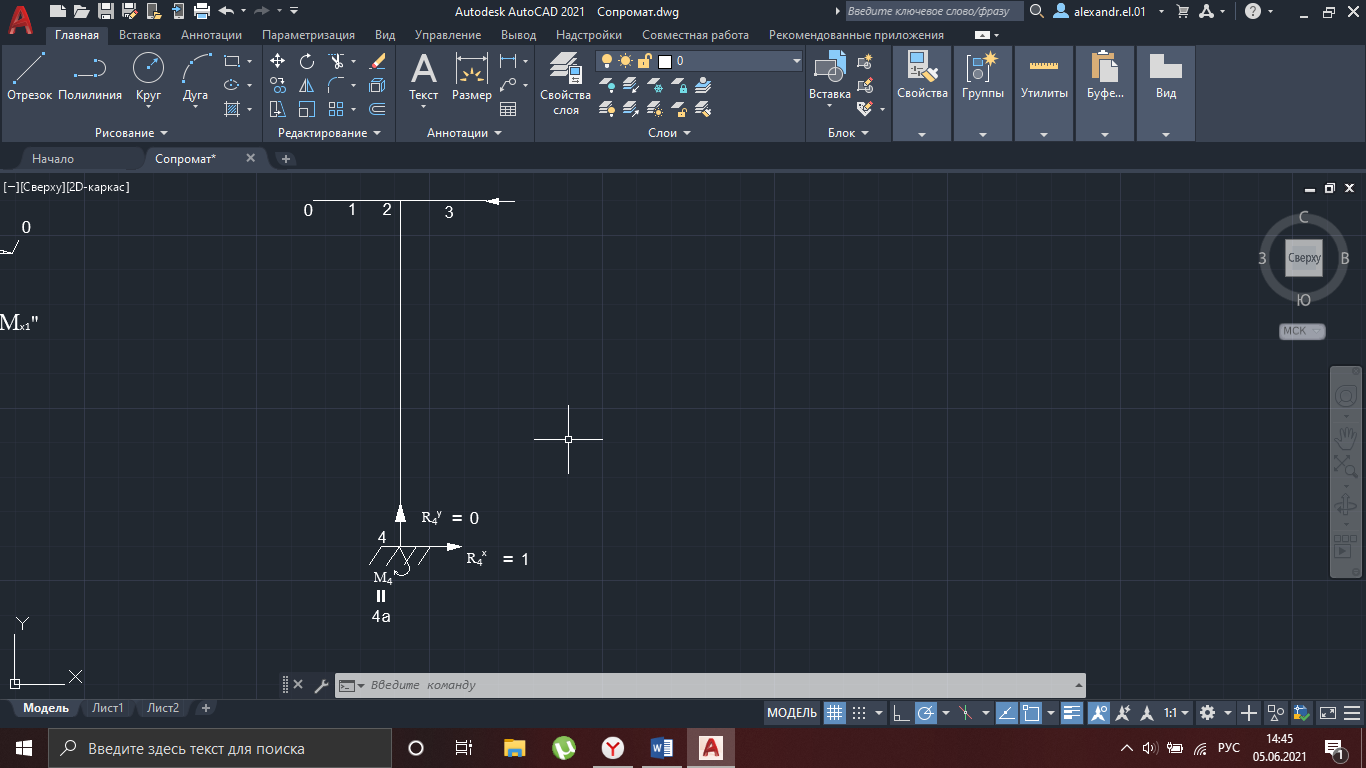
Рисунок 25
∑х = 0:
R4x = 1
∑y = 0:
R4y = 0
∑M4 = 0:
M4 + 4a = 0:
M4 = -4a
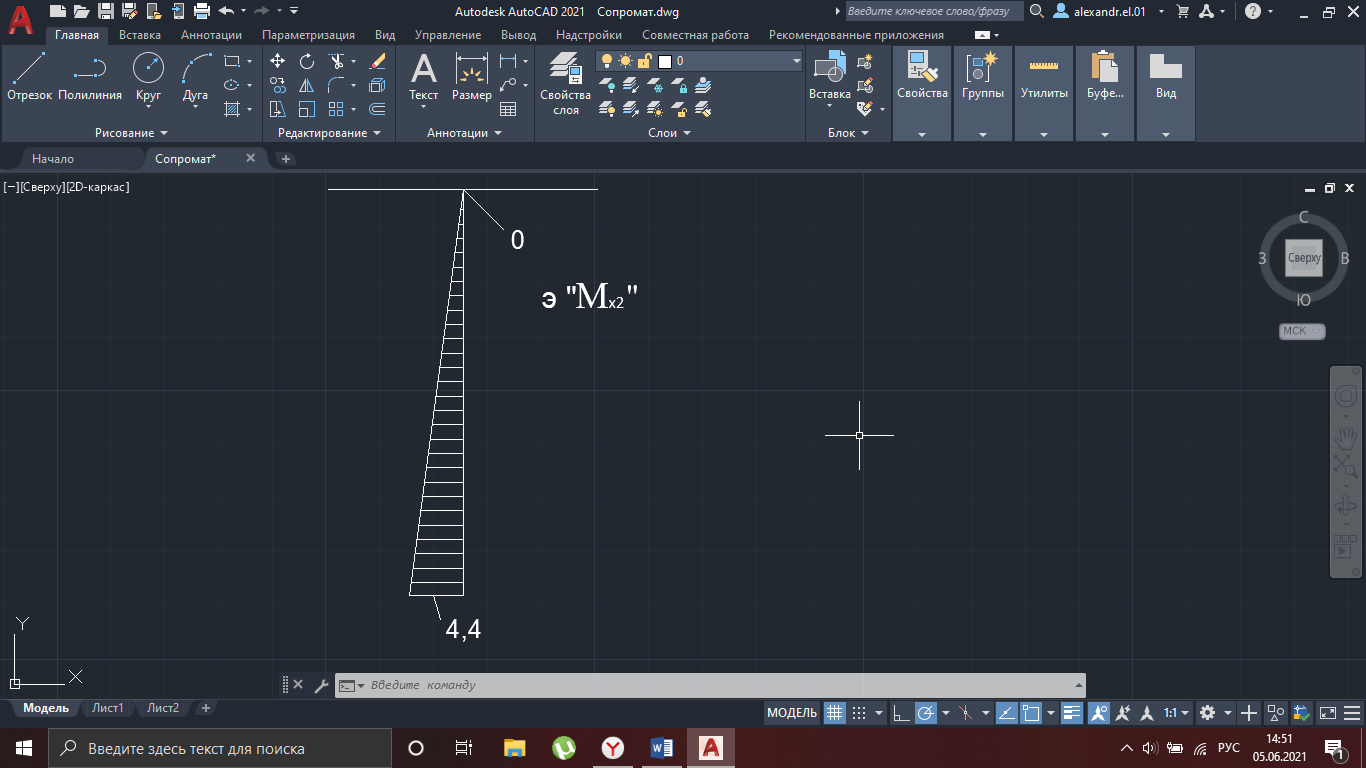
Рисунок 26
3.
δ11 =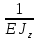 * [2.2*4*1.1*2.2 +
* [2.2*4*1.1*2.2 +  *2.2*2*1.1*
*2.2*2*1.1*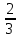 *2.2] =
*2.2] = 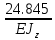 м
м
3
δ22 = *4,4*4*1,1*
*4,4*4*1,1* *4,4 =
*4,4 = 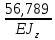 м3
м3
δ12 = δ21
δ12 = *2,2*4*1,1*
*2,2*4*1,1* *4,4 =
*4,4 = 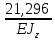 м3
м3
δ1p = *
*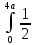 *
*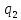 *
* *2a
*2a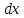 =
=  *
*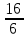 *2*1.1*
*2*1.1*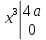 =
= 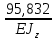 кН*м3
кН*м3
δ2p = *
*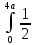 *
*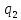 *
* *(4a-x)
*(4a-x)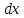 =
=  (
(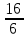 *4*1.1*
*4*1.1*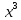 -
-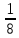 *16*
*16*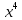 )
)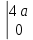 =
= 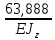 кН*м3
кН*м3
Тогда:
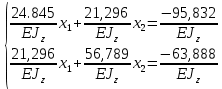 далее умножаем на
далее умножаем на 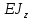
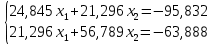
Решим полученную систему методом Гаусса:
Х1 = -4,269 кН
Х2 = 0,48 кН
4.
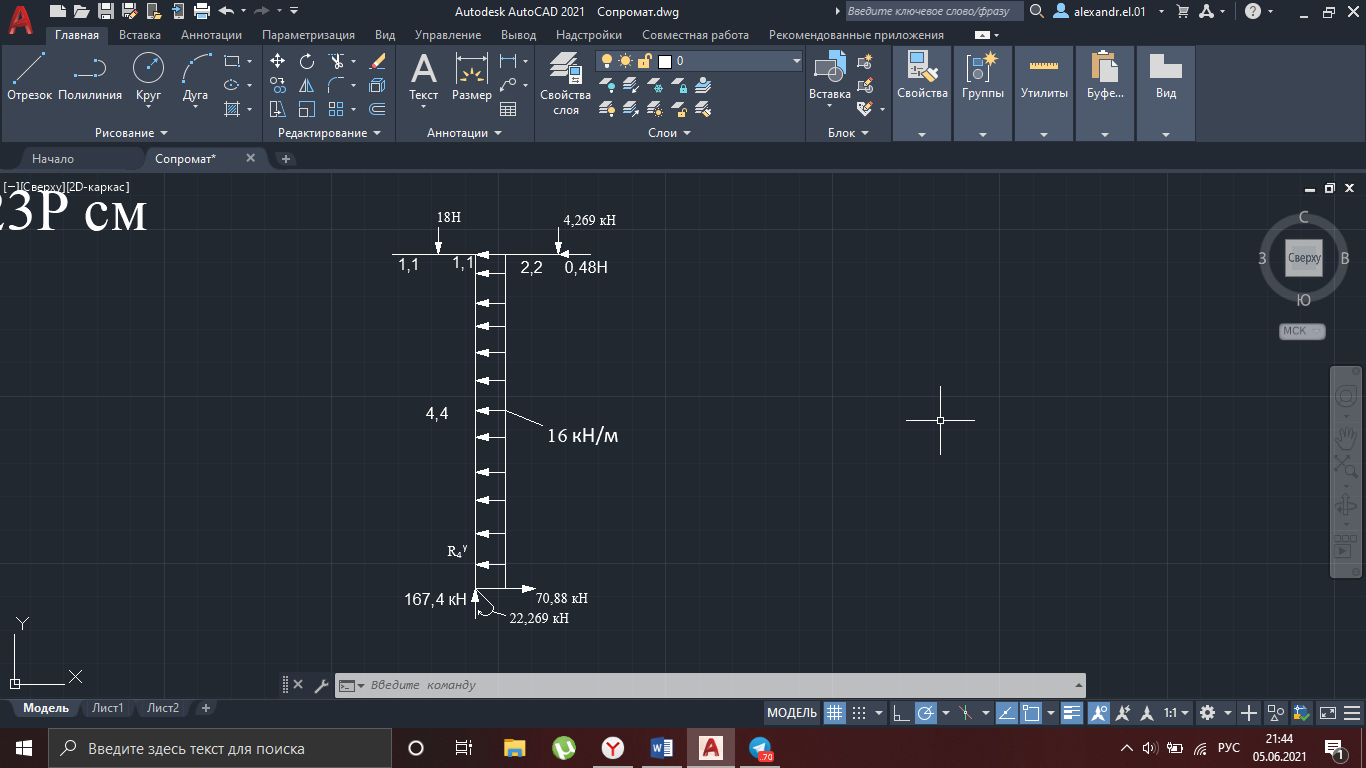
Рисунок 27
R4x = 70,4 + 0,48 = 70,88 кН
R4y = 18 + 4,269 = 22,269 кН
M4 = 174,68 – 2,2*4,269 + 4,4*0,48 = 1674 кН*м
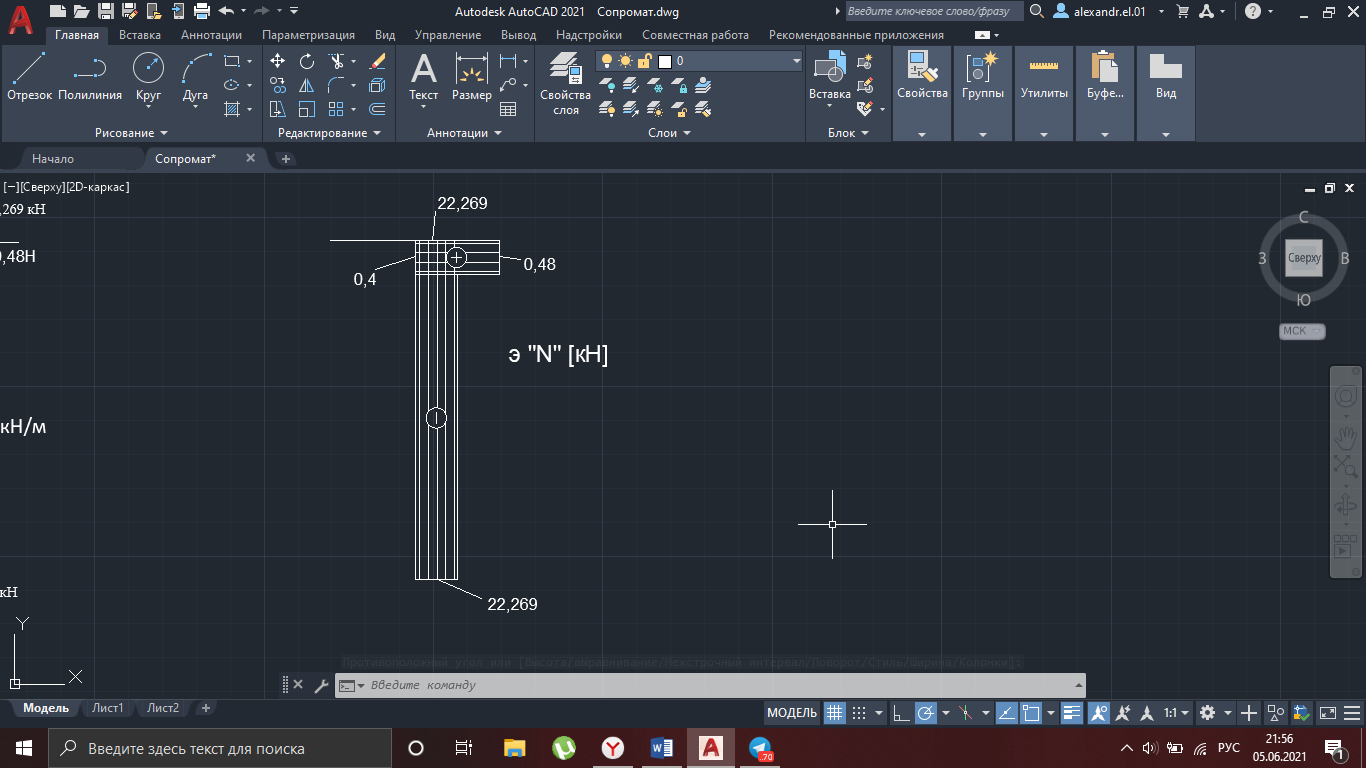
Рисунок 28
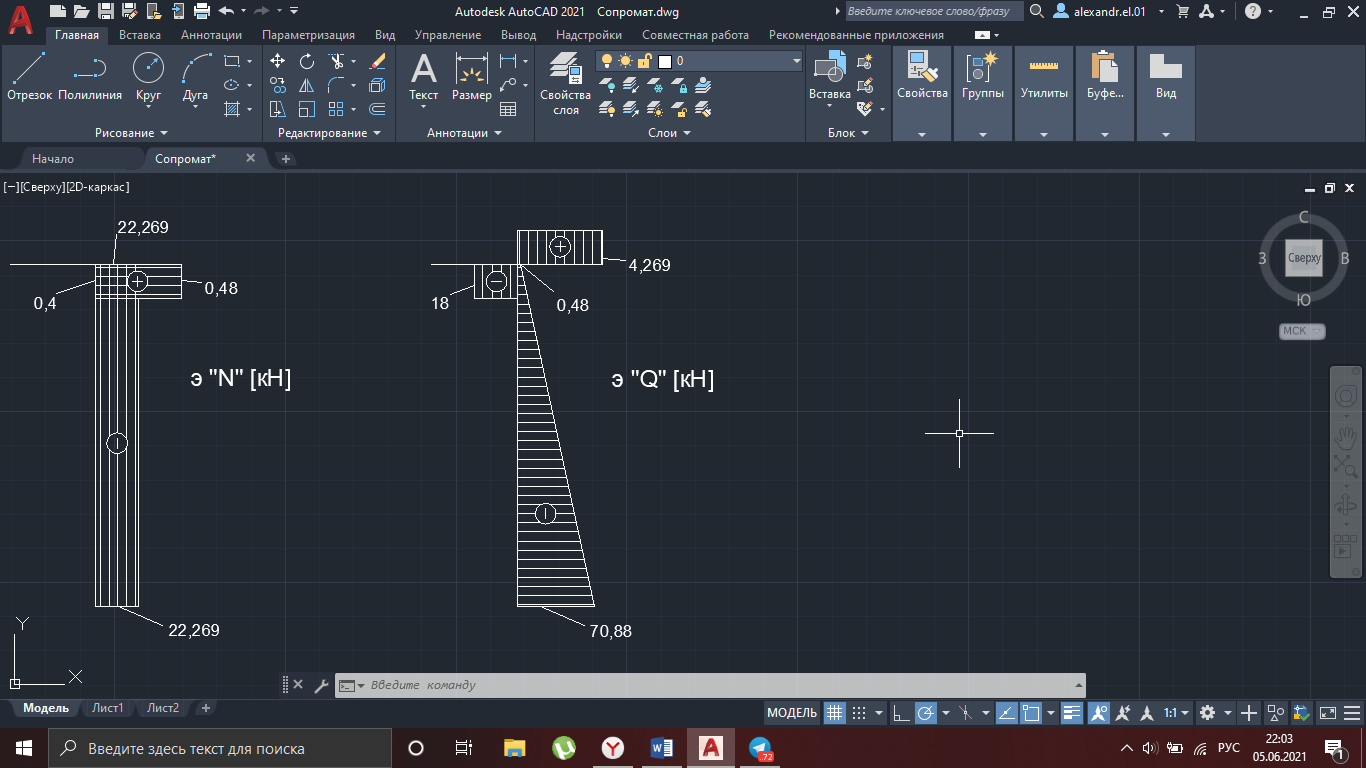
Рисунок 29
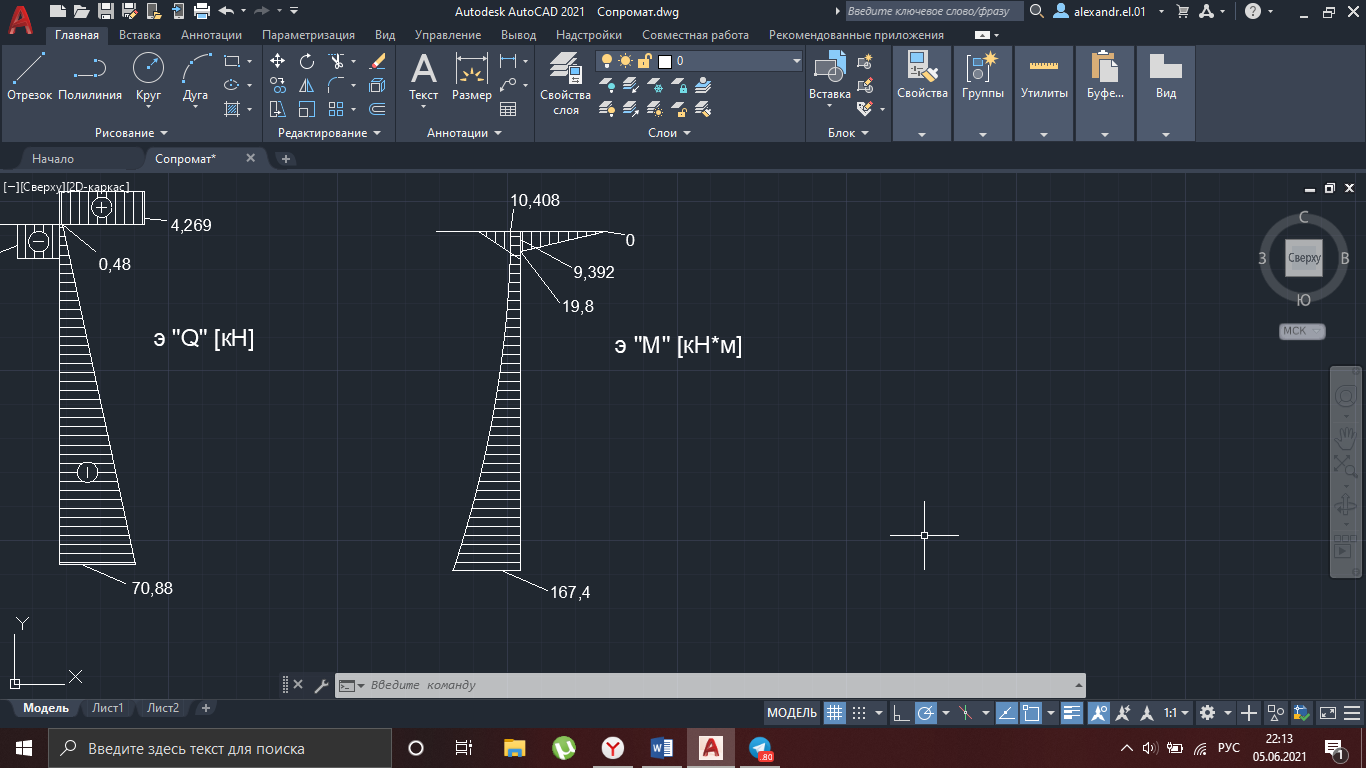
Рисунок 30
Определим угол поворота
∑m4 = 0:
M4 = 1
∑x = 0:
R4x = 0;
∑y = 0:
R4y = 0;
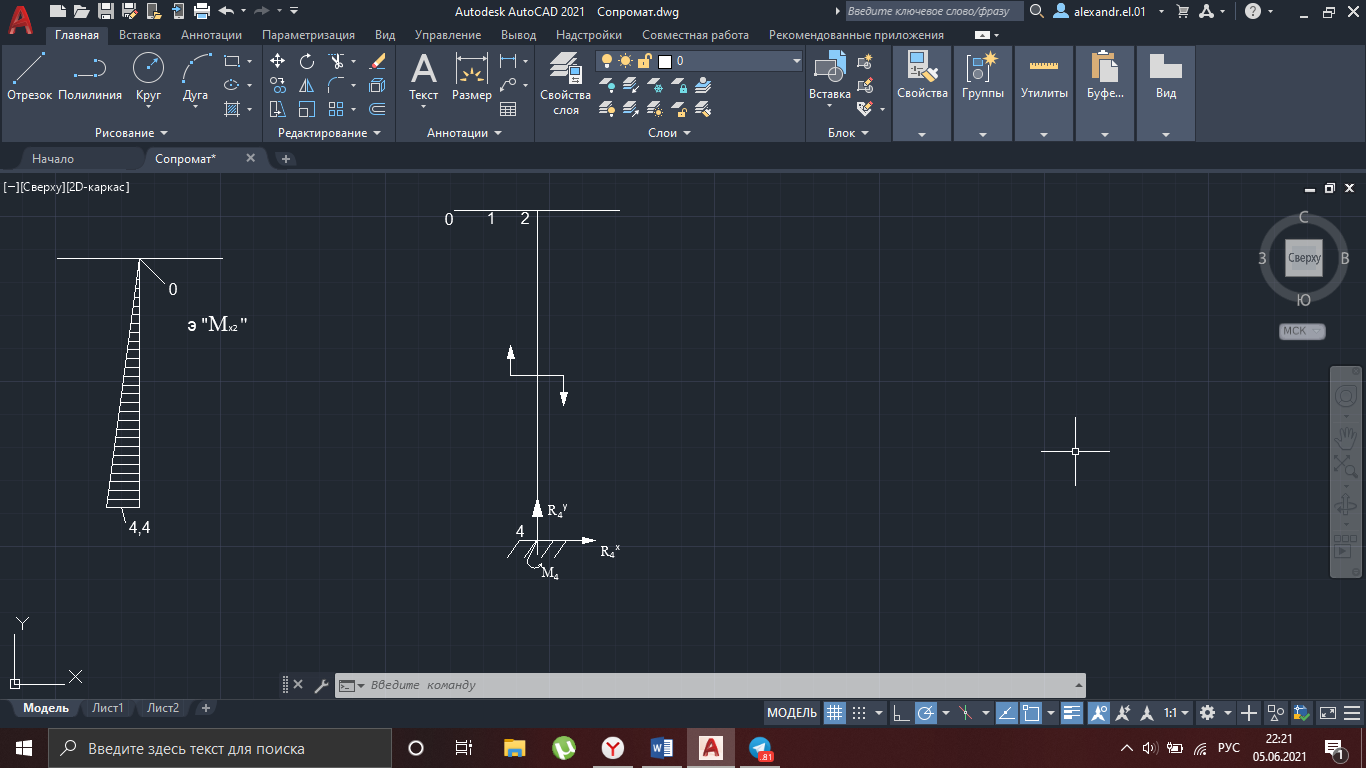
Рисунок 31
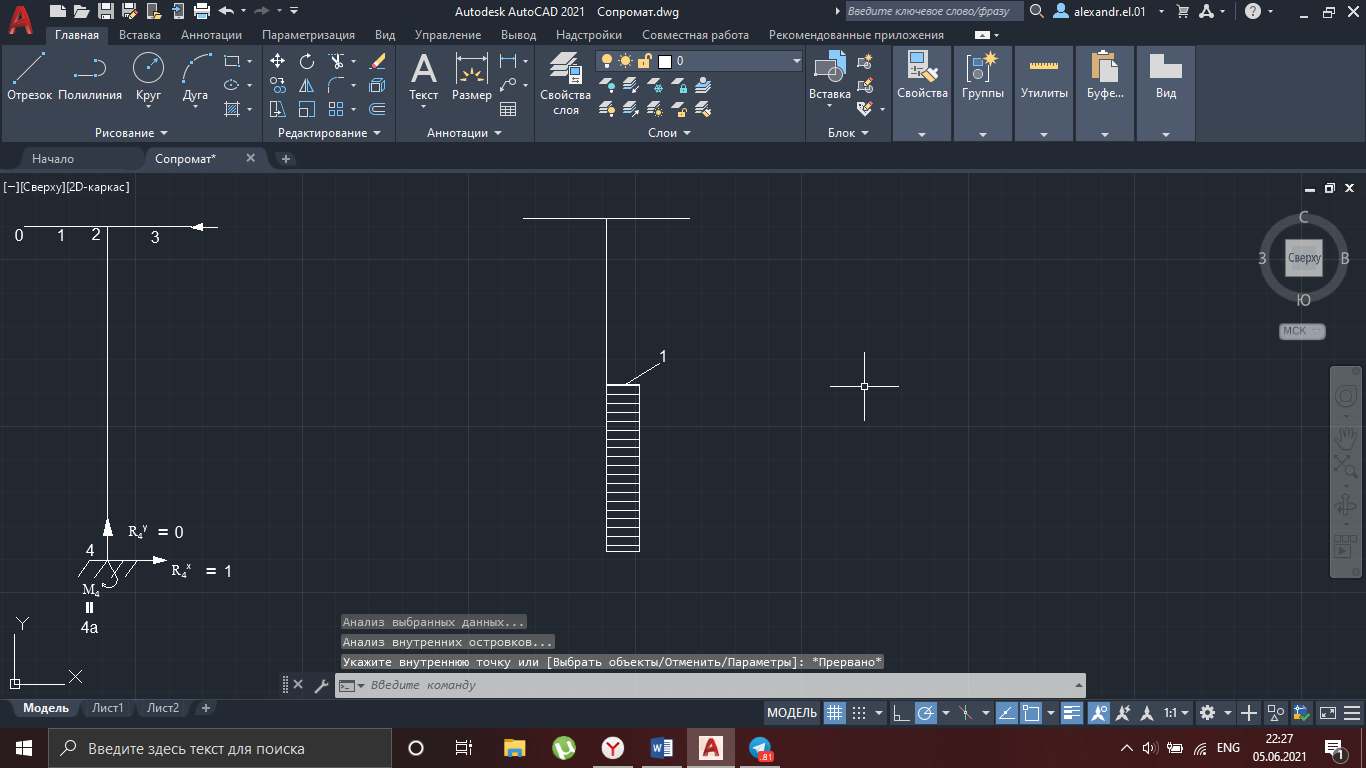
Рисунок 32
Ɵ =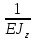 * [1*2a*(
* [1*2a*(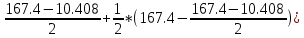 ] = =
] = =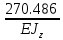
Подберём двутавровое сечение:
δmax =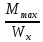 ≤ [δ] =>
≤ [δ] => 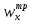 ≥
≥ 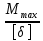 =
= 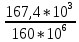 = 1046.25*
= 1046.25*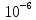 м3 = 1046.25 см3
м3 = 1046.25 см3
По ГОСТу 8239-89 подбираем двутавр №45:
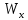 = 1231см3 >
= 1231см3 > 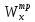
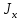 = 27696 см4
= 27696 см4
Расчет подмоторных балок на прочность при колебании.
Вариант №68
Дано:
Q1 = 900H ω = 530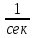 [σ] = 30 МПа
[σ] = 30 МПа
r = 0.25 мм Q = 2900 Н Схема №3б
l = 0.88 м βрез = 35
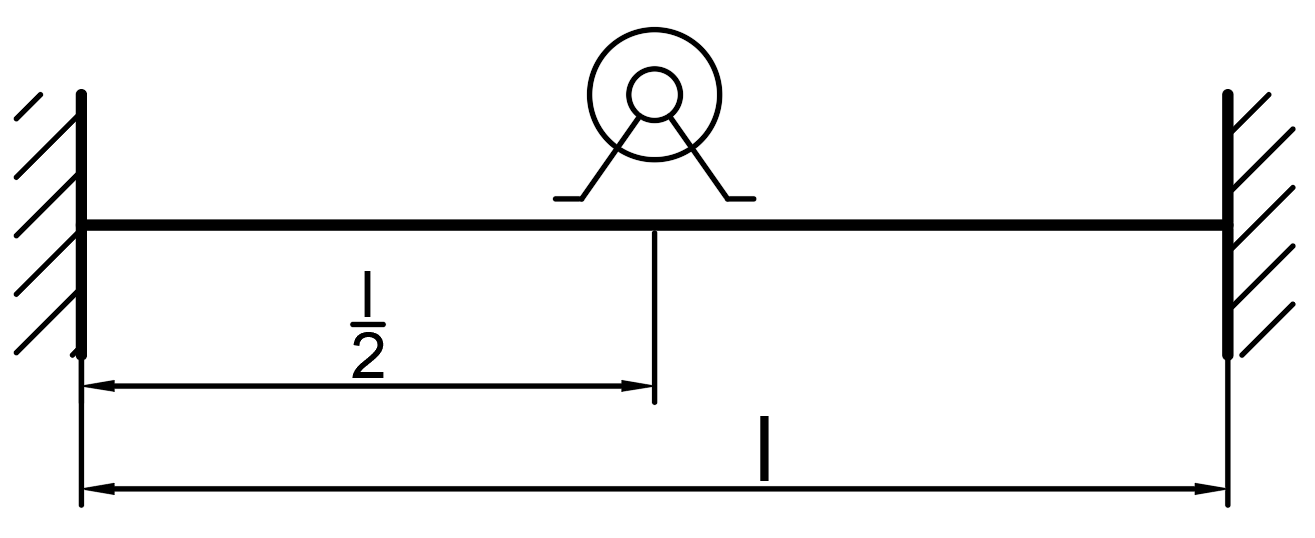
Рисунок 33 – Исходная схема
Начертим эпюру Мр от действия веса двигателя. Так как система один раз статически неопределима, то построим М1, приложив единичную силу вместо заменённой опоры.

Рисунок 34 – Эпюры
Составлю систему канонических уравнений. Так как неизвестная сила Х1 всего одна, то уравнение будет одно.
δ11Х1+Δ1р=0
Найду известные коэффициенты:
δ11=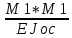 =
=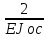 (
(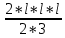 )=
)=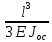
Δ1=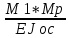 =
=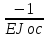 (
(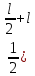 )
)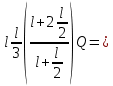 -
- 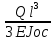
Подставлю их в исходное уравнение:
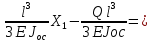 Х1=Q
Х1=Q
Подставлю Х1 в эквивалентную систему и построю эпюру М∑. Также построю эпюру М1к, заменив Q на единичную силу. Для нахождения δст необходимо перемножить М∑ и М1к.
δст=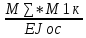 =
=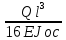
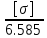 =
= 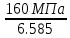 = 2429.7H
= 2429.7Hql₂ = 1.1P
q =
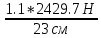 = 116.2
= 116.2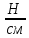
3.

Рисунок 17
Уч. 01
Условие прочности
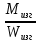 ≤ [σ]
≤ [σ]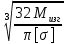 ≤ d
≤ dd ≥ 5.317 см
Уч. 12

Рисунок 18
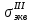 =
=  ≤ [σ]
≤ [σ]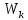 ≈ 0.2d3
≈ 0.2d3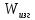 ≈ 0,1d3
≈ 0,1d3σ =
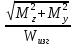
τ =
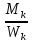
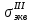 =
= 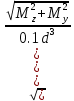 ≤ [σ]
≤ [σ]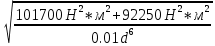 ≤ [σ]
≤ [σ]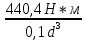 ≤ [σ] => d ≥
≤ [σ] => d ≥ 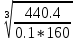 = 6 см
= 6 см-
Задача 2А
Расчет статически неопределимых систем при изгибе.
Вариант №68
Дано:
q2 = 16

Р1 = 18кН
а = 1,1м
Схема №11

Рисунок 19 – Исходная схема

Рисунок 20
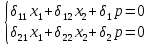
Построим грузовую эпюру:

Рисунок 21
Расчёты:
∑x = 0:
R4x = 4*q2*a = 70.4кН
∑y = 0:
R4y = R1 = 18кН
∑М4 = 0:
М4 + 4*q2*a * 2a + P1*a = 0
M4 = -8*16*1.12 – 18*1.1 = -174.68 кН*м

Рисунок 22
2.

Рисунок 23
∑х = 0:
R4x = 0
∑y = 0:
R4y = -1
∑M4 = 0:
M4 + 2a = 0:
M4 = -2a

Рисунок 24

Рисунок 25
∑х = 0:
R4x = 1
∑y = 0:
R4y = 0
∑M4 = 0:
M4 + 4a = 0:
M4 = -4a

Рисунок 26
3.
δ11 =
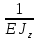 * [2.2*4*1.1*2.2 +
* [2.2*4*1.1*2.2 +  *2.2*2*1.1*
*2.2*2*1.1*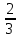 *2.2] =
*2.2] = 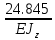 м
м
3
δ22 =
 *4,4*4*1,1*
*4,4*4*1,1* *4,4 =
*4,4 = 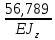 м3
м3δ12 = δ21
δ12 =
 *2,2*4*1,1*
*2,2*4*1,1* *4,4 =
*4,4 = 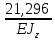 м3
м3δ1p =
 *
*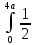 *
*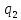 *
* *2a
*2a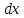 =
=  *
*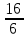 *2*1.1*
*2*1.1*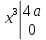 =
= 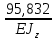 кН*м3
кН*м3δ2p =
 *
*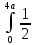 *
*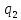 *
* *(4a-x)
*(4a-x)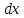 =
=  (
(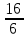 *4*1.1*
*4*1.1*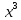 -
-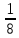 *16*
*16*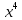 )
)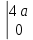 =
= 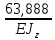 кН*м3
кН*м3Тогда:
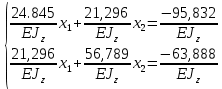 далее умножаем на
далее умножаем на 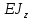
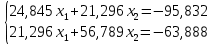
Решим полученную систему методом Гаусса:
Х1 = -4,269 кН
Х2 = 0,48 кН
4.

Рисунок 27
R4x = 70,4 + 0,48 = 70,88 кН
R4y = 18 + 4,269 = 22,269 кН
M4 = 174,68 – 2,2*4,269 + 4,4*0,48 = 1674 кН*м

Рисунок 28

Рисунок 29

Рисунок 30
Определим угол поворота
∑m4 = 0:
M4 = 1
∑x = 0:
R4x = 0;
∑y = 0:
R4y = 0;

Рисунок 31

Рисунок 32
Ɵ =
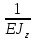 * [1*2a*(
* [1*2a*(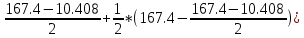 ] = =
] = =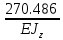
Подберём двутавровое сечение:
δmax =
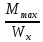 ≤ [δ] =>
≤ [δ] => 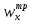 ≥
≥ 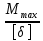 =
= 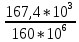 = 1046.25*
= 1046.25*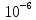 м3 = 1046.25 см3
м3 = 1046.25 см3По ГОСТу 8239-89 подбираем двутавр №45:
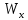 = 1231см3 >
= 1231см3 > 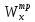
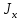 = 27696 см4
= 27696 см4-
Задание 2Б
Расчет подмоторных балок на прочность при колебании.
Вариант №68
Дано:
Q1 = 900H ω = 530
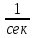 [σ] = 30 МПа
[σ] = 30 МПаr = 0.25 мм Q = 2900 Н Схема №3б
l = 0.88 м βрез = 35

Рисунок 33 – Исходная схема
Начертим эпюру Мр от действия веса двигателя. Так как система один раз статически неопределима, то построим М1, приложив единичную силу вместо заменённой опоры.

Рисунок 34 – Эпюры
Составлю систему канонических уравнений. Так как неизвестная сила Х1 всего одна, то уравнение будет одно.
δ11Х1+Δ1р=0
Найду известные коэффициенты:
δ11=
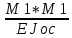 =
=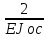 (
(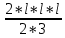 )=
)=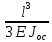
Δ1=
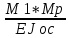 =
=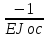 (
(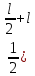 )
)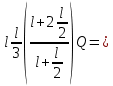 -
- 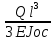
Подставлю их в исходное уравнение:
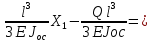 Х1=Q
Х1=QПодставлю Х1 в эквивалентную систему и построю эпюру М∑. Также построю эпюру М1к, заменив Q на единичную силу. Для нахождения δст необходимо перемножить М∑ и М1к.
δст=
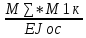 =
=