Файл: 1. Описание установки и методики измерений.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 116

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
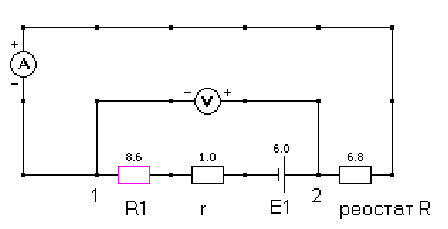
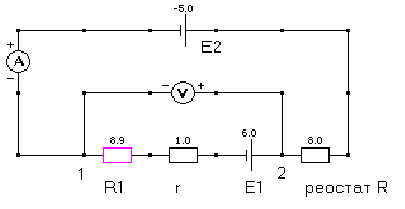
ВведениеЦелью работы является:- знакомство с компьютерным моделированием цепей постоянного тока;- экспериментальная проверка закона Ома для неоднородного участка цепи.1. Описание установки и методики измеренийРис. 1.1 – электрическая цепь (один источник тока)Рис. 1.2 – электрическая цепь (два источника тока)1.1. На рабочем столе монитора найдите ярлык программы «Открытая физика 1.1».Щелкните по ярлыку и запустите программу.1.2. Выберите: «Электричество и магнетизм», «Цепи постоянного тока».1.3. Внимательно ознакомьтесь с окном эксперимента. В левом нижнемуглы находятся кнопки «Элементы» - соединительный проводник, -источник тока, - резистор, - вольтметр, - амперметр, - кнопкадля установки значений резисторов и источников Э.Д.С.Внизу в средней части расположены кнопки «Счет» - для измерения силы тока иразности потенциалов в элементах цепи, «Очистить» - для очистки окна эксперимента.1.4. При собранной электрической цепи в окне эксперимента (Рис. 1.1, Рис. 1.2) можновыделить элемент цепи – источник тока или резистор. Для этого нужно нажать кнопку, подвести курсор в виде руки к элементу и щелкнуть по нему. При этом изменяетсяцвет элемента и в нижней части окна появляется окно с регулятором для установки значенийпараметра элемента. Регулятор можно перемещать, если подвести к нему курсор мыши иперемещать, удерживая нажатой левую кнопку мыши или, щелкая по соответствующейстрелке в окне регулятора.2. Основные расчётные формулыЗакон Ома для неоднородного участка 1-2 имеет видI∙(

+ r) = ( ) + (2.1)

Обозначим V = ( ) показания вольтметра. Выражение (2.1) принимает следующий вид:

I∙( + r) =V+ (2.2)

Запишем

V= I∙( + r) - (2.3)

= + r (2.4)

V= I∙ - (2.5)

График зависимости V = f(I) должен представлять прямую линию, причем угловой

коэффициент прямой равен сопротивлению участка цепи 1-2.

Координата точки пересечения продолжения прямой графика с осью ординат равна

значению Э.Д.С. на этом же участке

= (2.6)

I= 0, V= (2.7)

С учетом полярности вольтметра на схемах Рис. 2.2, Рис. 2.3 следует записать

V = ( ­ - ) (2.8)

(

) = -V (2.9)

При этом выражения (2.5) – (2.7) принимают вид

V= -I∙ + (2.10)

= - (2.11)

I= 0, V= (2.12)

( )эксп = - (2.13)

Относительная погрешность сопротивления

ε( )эксп = (2.14)

Выберите на графике произвольную точку, например, М. Определите ее координаты , . Подставьте значения , в формулу (2.10). Вычислите значение ()эксп и относительную погрешность ε()эксп по формулам

()эксп = + ∙( )эксп (2.15)

ε()эксп = (2.16)

3. Результаты работы и их анализ

Таблица 3.1


Номер измерения
R, Ом
V, В
I, А
Примечание

1
1
0.60
0.60
= 8 В

r = 2.4 Ом

= 10 Ом

2
2
1.11
0.56

3
3
1.56
0.52

4
4
1.95
0.49

5
5
2.30
0.46

6
6
2.61
0.43

7
7
2.89
0.41

8
8
3.14
0.39

9
9
3.36
0.37

10
10
3.57
0.36

( )эксп = 12.5 Ом
ε( )эксп= 0.008

()эксп =7.95 В
ε()эксп = 0.006
= + r = 10 + 2.4 = 12.4 Ом( )эксп = - ∆V = 3.4 – 0.9 = 2.5 B∆I = 0.37 – 0.57 = - 0.2 A( )эксп = - = 12.5 Омε( )эксп = = = = 0.008()эксп = + ∙( )эксп=1.2 В = 0.54 А()эксп = 1.2 + 0.54 ∙ 12.5 = 7.95 Вε()эксп = = = = 0.006Таблица 3.2

Номер измерения
R, Ом
V, В
I, А
Примечание

1
1
-4.49
1.01
= 8 В

= -5.5 B

r = 2.4 Ом

= 10 Ом

2
2
-3.62
0.94

3
3
-2.87
0.88

4
4
-2.21
0.82

5
5
-1.62
0.78

6
6
-1.10
0.73

7
7
-0.63
0.70

8
8
-0.21
0.66

9
9
0.18
0.63

10
10
0.53
0.6

( )эксп = 12 Ом
ε( )эксп= 0.03

()эксп = 7.6 В
ε()эксп = 0.05
( )эксп = - ∆V = - 4.4 – (- 2.6) = - 1.8 В∆I = 1 – 0.85 = 0.15 А( )эксп = - = 12 Омε( )эксп = = = = 0.03()эксп = + ∙( )эксп = -2 В = 0.8 А()эксп = - 2 + 0.8∙12 = - 2 + 9.6 = 7.6 Вε()эксп = = = = 0.054.ЗаключениеВ результате проделанной работы мы убедились в справедливости закона Ома для неоднородного участка цепи I∙( + r) = ( ) + , так как убедились, что графики являются прямыми линиями.

Смотрите также файлы