ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 27
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОР №2- «Тригонометрия» 9 класс алгебра 3 четверть
| Тема | Формулы привидения. Формулы синуса, косинуса, тангенса и котангенса суммы и разности двух углов. Формулы тригонометрических функций двойного и половинного углов. |
| Цель обучения | 9.2.4.4 Выводить и применять формулы приведения 9.2.4.3 Выводить и применять тригонометрические формулы суммы и разности углов, формулы двойного и половинного углов. |
| Критерий оценивания | Обучающийся
|
| Уровень мыслительных навыков | Применение |
| Время выполнения | 25 минут |
| Критерий оценивания | № задания | Дескриптор | Балл |
| Обучающийся | |||
| Применяет формулы приведения для упрощения и нахождения значения выражения | 1а | Представляют в виде формул приведения | 1 |
| Применяют формулы приведения | 1 | ||
| Находят значение выражения | 1 | ||
| 1b | Применяют формулы приведения | 1 | |
| Упрощают выражение | 1 | ||
| Находят значение | 1 | ||
| Применяет тригонометрические формулы суммы и разности углов | 2 | применяет формулу косинуса суммы двух углов/применяет формулу cинуса суммы двух углов | 1 |
| применяет формулу косинуса разности двух углов/применяет формулу cинуса разности двух углов | 1 | ||
| приводит подобные слагаемые | 1 | ||
| Применяет тригонометрические формулы двойного и половинного угла | 3а | находит значение синуса угла, учитывая четверть; | 1 |
| применяет формулу синуса двойного угла и находит его значение; | 1 | ||
| применяет формулу косинуса двойного угла и находит его значение. | 1 | ||
| 3b | находит значение косинуса угла, учитывая четверть; | 1 | |
| применяет формулу синуса половинного угла и находит его значение; | 1 | ||
| применяет формулу косинуса половинного угла и находит его значение. | 1 | ||
| Итого: | 15 | ||
Задания 1 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1350·cos2100·tg4050·ctg3900= b)
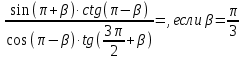
2. Докажите тождество: cos(α+β) + cos(α-β)=2cosαcosβ [3]
3. Найдите:
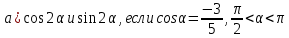 [6]
[6]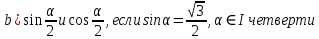
2 вариант
1.Упростите и найдите значение выражения: [6]
а) sin2100·cos1350·tg3900·ctg3000= b)
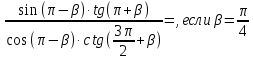
2. Докажите тождество: sin(α+β) + sin(α-β)=2sinαcosβ [3]
3. Найдите:
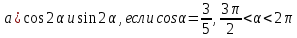 [6]
[6]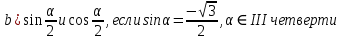
3 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1500·cos3150·tg2100·ctg4050= b)
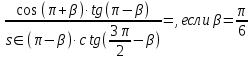
2. Докажите тождество: cos(α+β) - cos(α-β)=-2sinαsinβ [3]
3. Найдите:
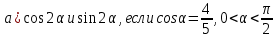 [6]
[6]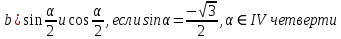
4 вариант
1.Упростите и найдите значение выражения: [6]
а) sin3150·cos1500·tg2100·ctg3000= b)
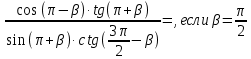
2. Докажите тождество: sin(α+β) - sin(α-β)=2cosαsinβ [3]
3. Найдите:
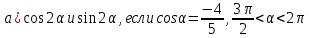 [6]
[6]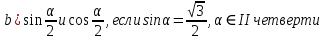
Задания 1 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1350·cos2100·tg4050·ctg3900= b)
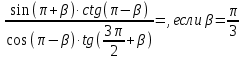
2. Докажите тождество: cos(α+β) + cos(α-β)=2cosαcosβ [3]
3. Найдите:
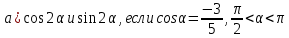 [6]
[6]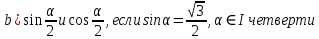
2 вариант
1.Упростите и найдите значение выражения: [6]
а) sin2100·cos1350·tg3900·ctg3000= b)
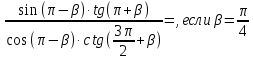
2. Докажите тождество: sin(α+β) + sin(α-β)=2sinαcosβ [3]
3. Найдите:
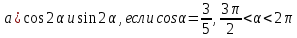 [6]
[6]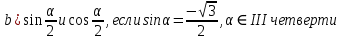
3 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1500·cos3150·tg2100·ctg4050= b)

2. Докажите тождество: cos(α+β) - cos(α-β)=-2sinαsinβ [3]
3. Найдите:
 [6]
[6]
4 вариант
1.Упростите и найдите значение выражения: [6]
а) sin3150·cos1500·tg2100·ctg3000= b)

2. Докажите тождество: sin(α+β) - sin(α-β)=2cosαsinβ [3]
3. Найдите:
 [6]
[6]
Задания 1 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1350·cos2100·tg4050·ctg3900= b)

2. Докажите тождество: cos(α+β) + cos(α-β)=2cosαcosβ [3]
3. Найдите:
 [6]
[6]
2 вариант
1.Упростите и найдите значение выражения: [6]
а) sin2100·cos1350·tg3900·ctg3000= b)

2. Докажите тождество: sin(α+β) + sin(α-β)=2sinαcosβ [3]
3. Найдите:
 [6]
[6]
3 вариант
1.Упростите и найдите значение выражения: [6]
а) sin1500·cos3150·tg2100·ctg4050= b)

2. Докажите тождество: cos(α+β) - cos(α-β)=-2sinαsinβ [3]
3. Найдите:
 [6]
[6]
4 вариант
1.Упростите и найдите значение выражения: [6]
а) sin3150·cos1500·tg2100·ctg3000= b)

2. Докажите тождество: sin(α+β) - sin(α-β)=2cosαsinβ [3]
3. Найдите:
 [6]
[6]