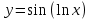Файл: 1. Выполнить деление комплексных чисел Деление комплексных чисел определяется как действие, обратное умножению.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 62
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
Математика
Группа Пг18М661
Студент
Савинов А.А.
МОСКВА 2021
1. Выполнить деление комплексных чисел:
Деление комплексных чисел определяется как действие, обратное умножению.
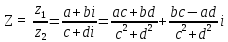
а)
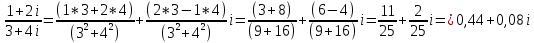
б)
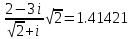
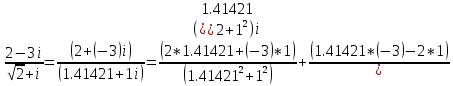
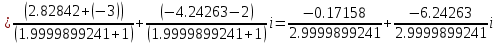
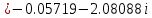
в)
+
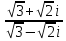
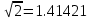
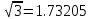
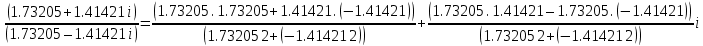
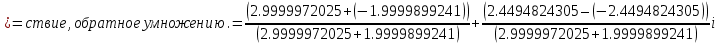
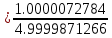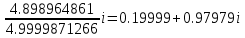
г)
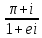
π = 3.14159
℮= 2.71828
+
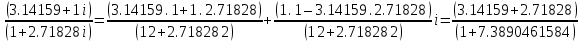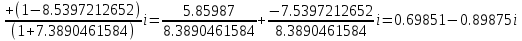
д)
=
=
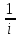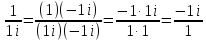-1i
е)
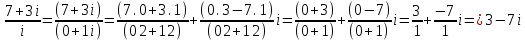
2. Вычислить пределы последовательностей:а)
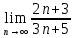
Разделим числитель и знаменатель на n:
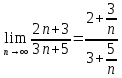При n→
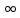значение каждой из дробей стремится к 0. Получается выражение: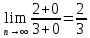 
б)
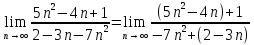
Разделим числитель и знаменатель на
: 
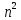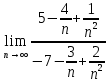
При n→
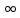значение каждой из дробей стремится к 0. Получается выражение: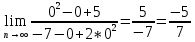 
в)
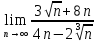
Вычислим с помощью метода Лопиталя.
У нас есть неопределенность типа
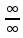, т.к. предел для числителя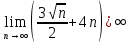 
и для знаменателя предел
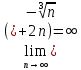
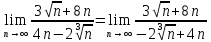
Преобразуем немного функцию под знаком предела
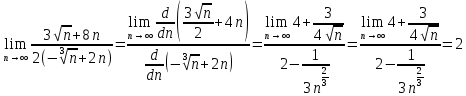
г)
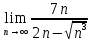
Вычислим с помощью метода Лопиталя.
У нас есть неопределенность типа
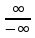, т.к. предел для числителя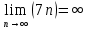 
и для знаменателя предел
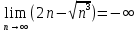
Преобразуем функцию под знаком предела:
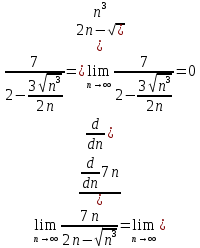
д)
-
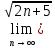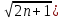
При n
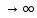
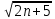
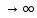
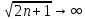, имеем предопределенность вида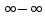 
Применим формулу
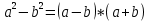
a=
)*(
)=
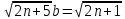
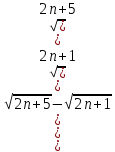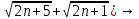
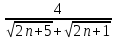
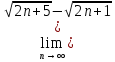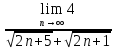= 0е)
-
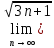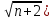
При n
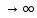
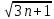
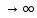
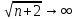, имеем предопределенность вида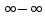 Применим формулу
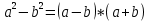
a=
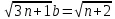
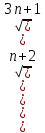3n+1-n-2=2n-1=
)*(
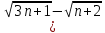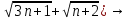
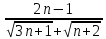
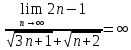
ж)
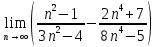по св-ву вычисления пределов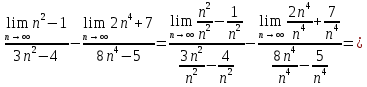
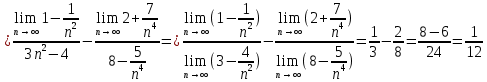
з)
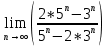
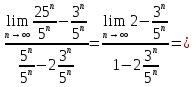
т.к. функция показательная
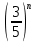0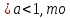
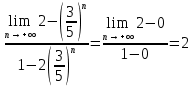
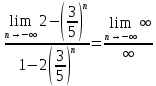
3. Используя признаки Даламбера и Коши исследовать сходимость рядов:
а)
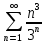
Признак Даламбера.
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).
= = =
Поскольку q < 1, то ряд сходится.
б)
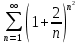
Применим радикальный признак Коши:
=
Поскольку полученное значение больше или равно 1, то ряд расходится.
в)
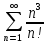
Признак Даламбера.
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).
= = =
Поскольку q < 1, то ряд сходится.
г)
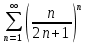
Применим радикальный признак Коши:
=
Поскольку полученное значение больше или равно 1, то ряд расходится.
д)
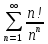
Признак Даламбера.
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).
= = =
Поскольку q < 1, то ряд сходится.
е)
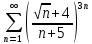
Применим радикальный признак Коши:
=
Поскольку полученное значение меньше 1, то ряд сходится.
4. Найти производные сложных функций.
1.
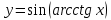
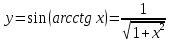следовательно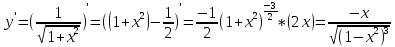
2.
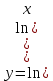
Производная сложной функции
=
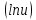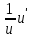
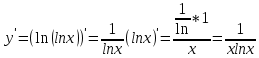
3.
= 
=
=
=
=
=
=
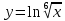
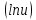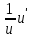
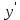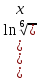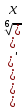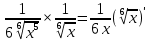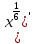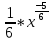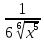
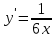
4.
(
=
=
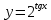
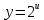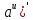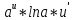
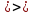
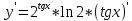
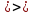
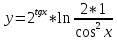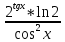
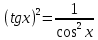
5.
= 
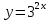
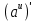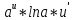
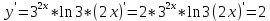
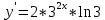
6.
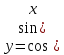
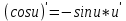
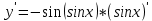
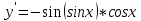
7.
