ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 97
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
2-11 Определите температуру абсолютно черного тела, при которой его энергетическая светимость равна 10 кВт/м2.
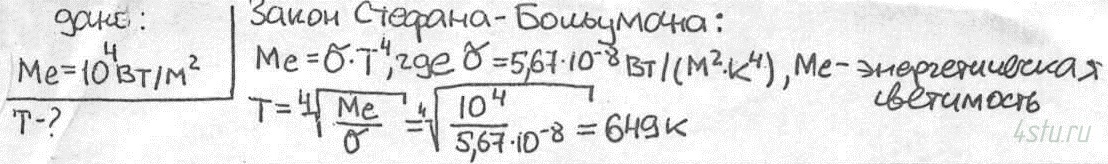
2-50 Определите максимальную скорость фотоэлектронов, вылетающих из металла с работой выхода 4,5 эВ под действием гамма-излучения с энергией квантов 1,53 МэВ.
ДОБАВИТЬ РАБОТУ ВЫХОДА

2-71 Определить границы спектральной области, в которой лежат линии серии Бальмера.
CПРОСИТЬ ЭТО ДЛИНА ВОЛНЫ ИЛИ НЕТ

Длины волн линий, принадлежащих серии Бальмера, определяются по формуле Бальмера:
где n=3,4,... Тогда границы серии найдем при n1=3 и n2=4.
1/l1=R(1/22-1/32)=5R/36; l1=36/5R.
1/l2=R(1/22-1/42)=R/4; l2=R/4
l1=36/(5*1,09*107)=6,6*10-7(м); l2=4/1,09*107=3,67*10-7(м).
Ответ: l1=6,6*10-7м; l2=3,67*10-7м.
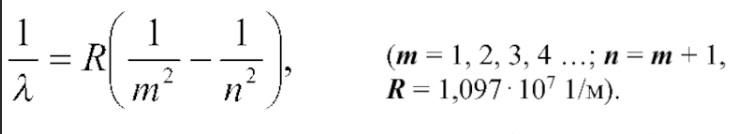
Серия Бальмера - это спектральная серия водорода, которая содержит видимые спектральные линии. Границы спектральной области, в которой лежат линии серии Бальмера, можно определить с помощью формулы Ридберга:
1/λ = R (1/2^2 - 1/n^2),
где λ - длина волны спектральной линии, R - постоянная Ридберга (R = 1,097 × 10^7 м^-1), n - целое число, которое определяет энергетический уровень электрона (n = 3, 4, 5, ...).
Для серии Бальмера мы рассматриваем электрон, переходящий с более высокого энергетического уровня (n > 2) на второй энергетический уровень (n = 2). Таким образом, мы ищем значения длины волны для n = 3, 4, 5, ...
Для n = 3, получаем:
1/λ = R (1/2^2 - 1/3^2) = 1,097 × 10^7 м^-1 × (1/4 - 1/9) = 1,097 × 10^7 м^-1 × 5/36 = 1,524 × 10^6 м^-1
λ = 1/1,524 × 10^6 м^-1 = 656,3 нм
Для n = 4, получаем:
1/λ = R (1/2^2 - 1/4^2) = 1,097 × 10^7 м^-1 × (1/4 - 1/16) = 1,097 × 10^7 м^-1 × 3/16 = 1,909 × 10^6 м^-1
λ = 1/1,909 × 10^6 м^-1 = 486,1 нм
Для n = 5, получаем:
1/λ = R (1/2^2 - 1/5^2) = 1,097 × 10^7 м^-1 × (1/4 - 1/25) = 1,097 × 10^7 м^-1 × 21/100 = 3,282 × 10^6 м^-1
λ = 1/3,282 × 10^6 м^-1 = 434,0 нм
Для n = 6, получаем:
1/λ = R (1/2^2 - 1/6^2) = 1,097 × 10^7 м^-1 × (1/4 - 1/36) = 1,097 × 10^7 м^-1 × 35/144 = 4,862 × 10^6 м^-1
λ = 1/4,862 × 10^6 м^-1 = 410,2 нм
Таким образом, линии серии Бальмера лежат в спектральной области от 410,2 нм до 656,3 нм, что соответствует фиолетовому, синему, зеленому и красному цветам.
2-110 Вычислить длину волны де Бройля для α- частицы, нейтрона и молекулы азота, движущихся с тепловой скоростью при температуре 30 С.
ВМЕСТО ЭЛЕКТРОНА ПОДСТАВИТЬ АЛЬФА ЧАСАТИЦУ

Длина волны де Бройля связана с импульсом частицы следующим соотношением:
λ = h / p,
где λ - длина волны, h - постоянная Планка, p - импульс частицы.
Для альфа-частицы имеем:
m = 6,64 × 10^-27 кг - масса альфа-частицы
v = √(3kT/m) - тепловая скорость альфа-частицы при температуре T
k = 1,38 × 10^-23 Дж/К - постоянная Больцмана
T = 30 + 273 = 303 К - температура в Кельвинах
Импульс альфа-частицы равен:
p = mv
p = 6,64 × 10^-27 кг × √(3 × 1,38 × 10^-23 Дж/К × 303 К / 6,64 × 10^-27 кг)
p = 1,28 × 10^-22 кг м/с
Длина волны де Бройля для альфа-частицы:
λ = h / p
λ = 6,63 × 10^-34 Дж с / 1,28 × 10^-22 кг м/с
λ = 5,17 × 10^-12 м
Для нейтрона имеем:
m = 1,67 × 10^-27 кг - масса нейтрона
v = √(3kT/m) - тепловая скорость нейтрона при температуре T
k = 1,38 × 10^-23 Дж/К - постоянная Больцмана
T = 30 + 273 = 303 К - температура в Кельвинах
Импульс нейтрона равен:
p = mv
p = 1,67 × 10^-27 кг × √(3 × 1,38 × 10^-23 Дж/К × 303 К / 1,67 × 10^-27 кг)
p = 3,30 × 10^-21 кг м/с
Длина волны де Бройля для нейтрона:
λ = h / p
λ = 6,63 × 10^-34 Дж с / 3,30 × 10^-21 кг м/с
λ = 2,00 × 10^-10 м
Для молекулы азота имеем:
m = 2 × 14,01 × 1,67 × 10^-27 кг - масса молекулы азота
v = √(3kT/m) - тепловая скорость молекулы азота при температуре T
k = 1,38 × 10^-23 Дж/К - постоянная Больцмана
T = 30 + 273 = 303 К - температура в Кельвинах
Импульс молекулы азота равен:
p = mv
p = 2 × 14,01 × 1,67 × 10^-27 кг × √(3 × 1,38 × 10^-23 Дж/К × 303 К / (2 × 14,01 × 1,67 × 10^-27 кг))
p = 1,37 × 10^-23 кг м/с
Длина волны де Бройля для молекулы азота:
λ = h / p
λ = 6,63 × 10^-34 Дж с / 1,37 × 10^-23 кг м/с
λ = 4,83 × 10^-11 м
2-131 Определите, сколько процентов начального количества радиоактивных ядер распадается за время, равное двум периодам полураспада.
За каждый период полураспада количество радиоактивных ядер уменьшается в два раза. Значит, после первого периода полураспада останется 50% от начального количества ядер, а после второго периода полураспада - 25%.
Таким образом, за время, равное двум периодам полураспада, распадется 50% + 25% = 75% начального количества радиоактивных ядер. Остается 25% от начального количества.
N=N0*2(-t/T) закон радиоактивного распада
N количество оставшихся ядер
N0 начальное количество ядер
T период полураспада
t время
N/N0=2^(-2T/T)=2^(-2)=1/4=0.25 это доля оставшихся атомов ( или 25%)
тогда 1-0,25=0,75 доля распавшихся (или 75%)
2-87 Во сколько раз длина волны линии Кα меньше длины волны линии Lα в
характеристическом рентгеновском спектре молибдена (Z = 42)? Постоянная экранирования для L-серии σL=7,5, для К-серии σK = 1
| Дано: Z 42 σL=7,5 σK = 1 | Решение: Применим формулу закона Мозли для Кα и Lα – линий 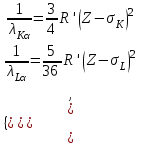 где R’ – штрихованная постоянная Ридберга, Z – атомный номер элемента, σ – постоянная экранирования. Разделим верхнее уравнение системы на нижнее: 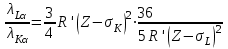 После упрощения: 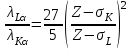 Подставим числовые значения: 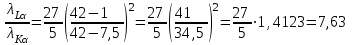 Ответ: 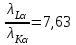 |
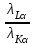 - ? - ? |