Файл: С. С. Поддубный должность, уч степень, звание подпись, дата инициалы, фамилия контрольная работа обнаружение радиосигналов по дисциплине Статистическая радиотехника.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 56
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
| КАФЕДРА 22 |
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
| к.т.н. , доцент | | | | С.С.Поддубный |
| должность, уч. степень, звание | | подпись, дата | | инициалы, фамилия |
| КОНТРОЛЬНАЯ РАБОТА |
Обнаружение радиосигналов |
| по дисциплине: Статистическая радиотехника |
РАБОТУ ВЫПОЛНИЛ
| СТУДЕНТ ГР. | Z9221 | | | | В.С. Смирнов | |||
| | номер группы | | подпись, дата | | инициалы, фамилия | |||
| | | | | | ||||
| | |
Санкт-Петербург 2023
Корреляционный обнаружитель
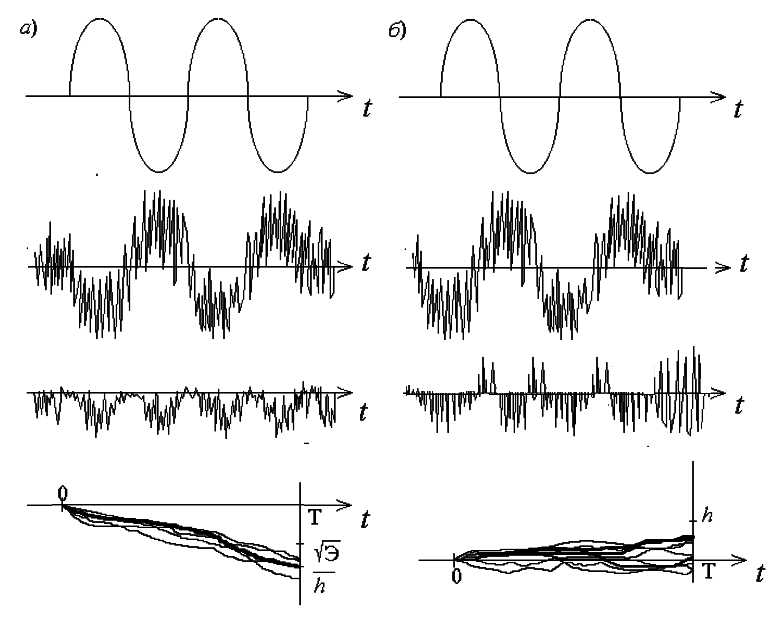
Рисунок 1-а) сигналы в противофазе,б) разница фаз сигналов π-4.
Фильтровой обнаружитель полностью известного сигнала
Более удобным с практической точки зрения является устройство, которое обеспечило бы формирование значения корреляционного интеграла для любого
Здесь учтено, что подынтегральное выражение в уравнении (3) отлично от нуля только на интервале времени, содержащем копию полезного сигнала Sa(t), поэтому значение корреляционного интеграла не изменяется при расширении времени наблюдения от -∞ до ∞. Интеграл (5) соответствует математической операции интегральной свёртки. В то же время из теории линейных электрических цепей известно, что интеграл свёртки выражает напряжение на выходе линейного фильтра, импульсная характеристика которого равна h(τ)=Sa(υ-τ), (6)
что соответствует зеркальному отображению функции Sa(τ) относительно прямой, проходящей через точку τ =υ / 2.
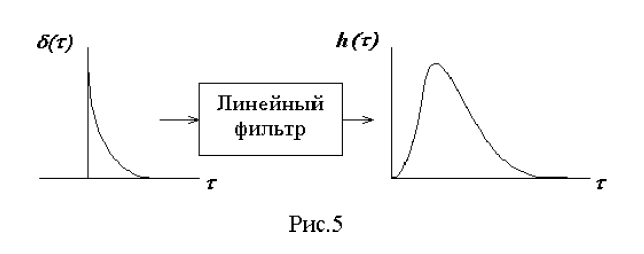
Импульсная характеристика линейного фильтра описывает реакцию
системы на входное воздействие в виде единичного импульса δ(τ), поданного в момент времени τ =0, и принимает отличные от нуля значения лишь при τ ≥ 0, так как следствие не возникает раньше вызывающей его причины (рис. 5).
Построение графика Sa(υ-τ) показано на рис.6,а. Кривая Sa(-τ) является
зеркальным отражением сигнала Sa(τ) с осью ординат в качестве оси симметрии.
Функция Sa(υ-τ), сдвинутая относительно Sa(-τ) на величину υ вправо, также зеркальна по отношению к сигналу Sa(τ), но с осью симметрии, проходящей через точку υ /2 на оси абсцисс. Для простоты рассмотрим случай, когда полезный сигнал является видеосигналом.
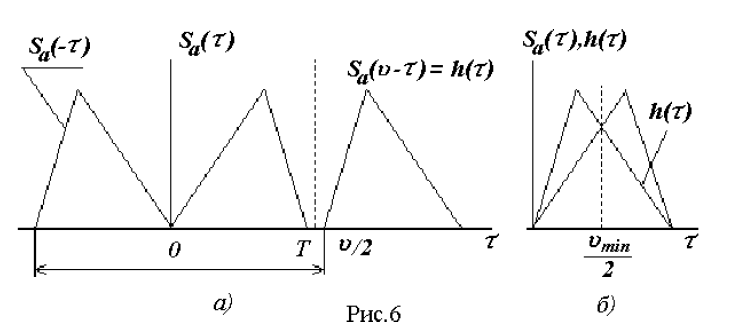
Поскольку импульсная характеристика не может начинаться при τ ≤ 0, то, очевидно, что задержка υ должна быть больше или равна длительности
полезного сигнала Т. Причём разные значенияυсоответствуют различным фильтрам. Импульсная характеристика фильтра с минимальной задержкойиυmin показана на рис. 6,б.
Выходное напряжение фильтра в момент времени t может быть представлено в виде
где С- коэффициент усиления фильтра.
Подставим в уравнение (7) выражение импульсной характеристики в виде (6), тогда напряжение на выходе фильтра будет иметь вид
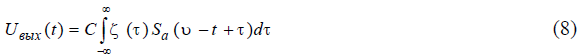
Сравнение соотношений (5) и (8) показывает, что для решения поставленной задачи достаточно соблюдения условия равенства аргументов при Sa(τ)
υ−t+τ =τ −t З , (9)
откуда получим значение текущего момента времени t, при котором равны между собой правые части выражений (5) и (8)
t=υ+t З . (10)
Таким образом, мы получили требуемый результат; выходное напряжение фильтра с импульсной характеристикой вида (6) в момент времени υ+tз равно, с точностью до масштабного множителя С, значению корреляционного интеграла для времени запаздывания
Uвых(υ+tз)=СZ(tз). (11)
Величины С и υ - постоянные, определяемые параметрами фильтра.
Вполне естественно желание сформировать значение ζ(tз) как можно раньше, поэтому используют, как правило, фильтры с минимальной задержкой υmin= T.
При этом напряжение на выходе фильтра равно (при С = 1) значению корреляционного интеграла в момент окончания полезного сигнала t=T. Такой фильтр позволяет реализовать оптимальный алгоритм обнаружения сигнала (3) и называется оптимальным фильтром.
Передаточная характеристика фильтра связана с его импульсной характеристикой преобразованием Фурье
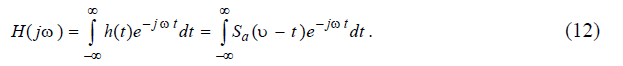Введём обозначение τ = υ - t и полагая υ = Т, перепишем (12) в виде
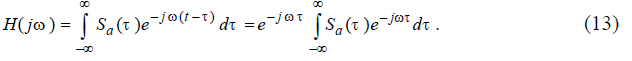Так как спектр полезного сигнала
то можно уравнение (13) представить в виде
Таким образом, передаточная характеристика фильтра должна с точностью
до постоянного множителя e-jωT совпадать с комплексно-сопряжённым спектром полезного сигнала [2,4]. Поэтому такой фильтр называется согласованным с сигналом Sa(t) или просто согласованным фильтром.
Физически воздействие амплитудно-частотной характеристики фильтра на
сигнал и шумовую помеху характеризуется тем, что на выходе фильтра в большей степени подавляются те спектральные составляющие входной смеси сигнала и помехи
, на которых меньше спектральная плотность полезного сигнала, т.е. меньше соотношение сигнал/помеха. В результате ослабление сигнала из-за неравномерности амплитудно-частотной характеристики фильтра будет выражено в меньшей степени, чем ослабление помехи, и соотношение сигнал/помеха на выходе возрастает и достигает при использовании согласованного фильтра своего максимально возможного значения [4].
Воздействие фазочастотной характеристики согласованного фильтра можно пояснить, если представить спектр входного полезного сигнала S(t) в виде
где S(ω) и ϕs(ω)- амплитудно- и фазочастотные характеристики спектра
полезного сигнала.
Тогда, согласно (15), передаточная характеристика согласованного
фильтра будет иметь вид
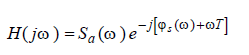
Полезный сигнал на выходе фильтра
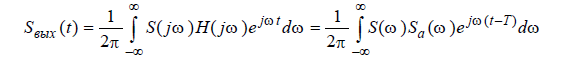достигает своего максимального значения в момент t=T, когда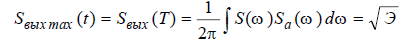
Если рассмотреть форму полезного сигнала на выходе фильтра Sвых(t), то оказывается, что она совпадает с точностью до постоянного множителя с автокорреляционной функцией полезного сигнала (рис.7), т.е. согласованный
фильтр существенно искажает входной полезный сигнал. Однако это не является в данном случае недостатком, так как задачей фильтра является не точное воспроизведение полезного сигнала, а обеспечение наилучшего его обнаружения на фоне помехи.
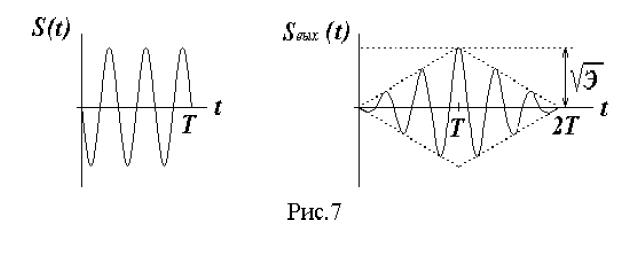
Структурная схема оптимального обнаружителя с согласованным фильтром показана на рис. 8.
Согласованный фильтр не реагирует на начальную фазу полезного сигнала, но её необходимо знать для управления моментом сравнения напряжения на выходе фильтра с порогом. Момент этот для фильтра с минимальной задержкой должен точно соответствовать окончанию полезного сигнала, при этом отношение сигнал/помеха на выходе фильтра максимально.
Изменение выходного напряжения фильтра при различных гипотезах показано на рис. 9,а,б.
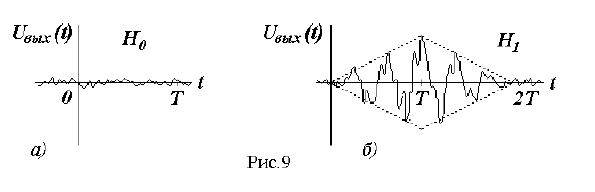
При действии только помехи (гипотеза H0) напряжение на выходе фильтра представляет собой стационарный случайный процесс. Причём, если помеха является нормальным “белым“ шумом, то шум на выходе линейного фильтра (рис.9,а) остаётся нормальным и имеет корреляционную функцию, совпадающую по форме с корреляционной функцией полезного сигнала. При справедливости гипотезы H1 в выходном напряжении фильтра дополнительно появляется сигнальная составляющая, совпадающая с корреляционной функцией полезного сигнала (см. рис. 7). После окончания действия полезного сигнала напряжение на выходе фильтра спадает (в отличие от выходного напряжения коррелятора, которое сохраняется сколь угодно долго).
Согласованный фильтр существенно отличается от коррелятора характером изменения напряжения помех на выходе. До момента появления копии полезного сигнала (t<0) напряжение помех на выходе коррелятора равно нулю, при воздействии копии (0 ≤ t ≤ T) - представляет собой нестационарный случайный процесс с увеличивающейся дисперсией (рис. 2), затем до момента “сброса” является постоянной величиной. При использовании согласованного фильтра помеха может действовать на входе достаточно долго, на выходе имеет место установившийся случайный процесс с постоянной дисперсией.
Оказывается, что отношение сигнал/помеха в момент окончания действия
полезного сигнала для коррелятора и для согласованного фильтра одно и то же, так как на их выходах напряжения за счёт действия сигнала одинаковы, а дисперсия нестационарного случайного процесса на выходе коррелятора достигает в момент окончания полезного сигнала значения дисперсии стационарного случайного процесса на выходе согласованного фильтра.
Различие в работе коррелятора и согласованного фильтра не проявляется, если их выходы использовать только в момент окончания действия полезного сигнала.
Основное отличие коррелятора от согласованного фильтра состоит в том, что при прохождении полезного сигнала (без помехи) на выходе коррелятора получается значение автокорреляционной функции полезного сигнала, соответствующее нулевому сдвигу по времени между сигналом и его копией, когда значение автокорреляционной функции максимально. На выходе согласованного фильтра при действии полезного сигнала формируется напряжение, соответствующее по форме всей автокорреляционной функции полезного сигнала (см.рис.7). В момент окончания сигнала на выходе согласованного фильтра так же, как и в корреляторе, сформируется максимальное значение функции автокорреляции полезного сигнала.