ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение
высшего профессионального образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
Кафедра 22
ОЦЕНКА ПРАКТИЧЕСКОЙ РАБОТЫ
| РУКОВОДИТЕЛЬ | | | | | ||||||
| | доктор. техн. наук, доцент | | | | | В.Ю. Волков | ||||
| | должность, уч. степень, звание | подпись, дата | | инициалы, фамилия | | |||||
ПРАКТИЧЕСКАЯ РАБОТА
по дисциплине: Основы искусственного интеллекта в радиотехнических системах
| Работу выполнил | | | | | | | | | | | | |||||
| студент гр. | Z9221 | | | М. М. Хоменок | | |||||||||||
| | | | | | | | | | | | | |||||
| | | | подпись, дата | инициалы, фамилия | | |||||||||||
Санкт-Петербург
2023
Исследование шумового поля
Дано:
Гауссовское шумовое поле со следующими параметрами: mu=30
stdev=30
K=1
mu-математическое ожидание,
Stdev- среднеквадратичные (стандартные) отклонения
K - число суммируемых полей
Экспоненциальное поле со следующими параметрами:
b = 30
K = 1
b- параметр масштаба поля
K- количество независимых реализаций поля
Поле с распределением Рэлея со следующими параметрами:
а=2
b=30
К=1
b- это индексы ложной тревоги и правильного обнаружения
Исследование будет осуществляться на прямоугольной матрице точек размером 256х256. Таким образом, сформированное шумовое поле содержит 65536 выборочных значений яркости. Каждая строка содержит 256 выборок.
Требуется:
изучить математическое ожидание, дисперсию, коэффициент асимметрии и эксцесса для выбранной или предложенной негауссовской модели по двум заданным параметрам так, ориентируясь на значение мощности СВ. Вдобавок исследовать сходимость выборочных оценок характеристик поля к теор. Значениям
Теоретическое исследование
Высчитать дисперсию
Гауссовское шумовое поле
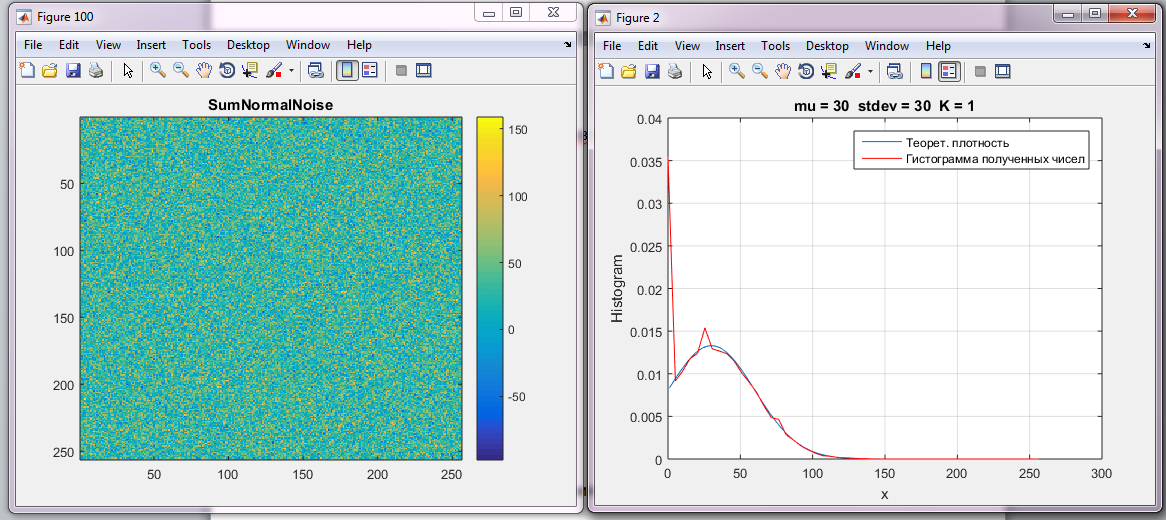
Рис. 1.1 Суммарное гауссовское поле размером 256 х 256 для mu=30, stdev=30, K=1

Рис. 1.2 Гистограмма и плотность распределения
На графике пиковое значение на 30 и выброс там же. Пик графика соответствует среднему значению шума, а ширина колокола - стандартному отклонению данных.
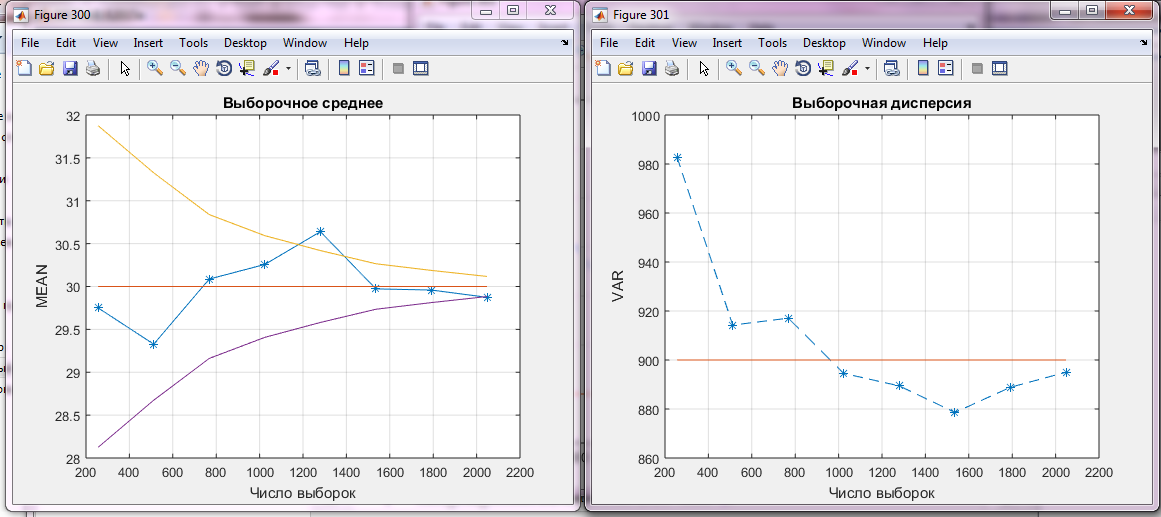
Рис 1.3 Зависимость выборочного среднего от числа выборок (доверительные интервалы mu ± stdev/√N при известных параметрах плотности)
На графике мы видим, что при увеличении числа выборок выборочное среднее приближается к теоретическим значениям параметров, однако на значении 1280 идет, начинается отклонение от теоретических значений. Тем самым подтверждается то, что с увеличением числа выборок мы приближаемся к теоретическим значениям параметров.

Рис 1.4 Выборочная дисперсия
На графике видно, с увеличением числа выборок выборочная дисперсия так же приближается к теоретическим значениям параметров, но так как выборочная дисперсия сильно зависит от выбросов, она имеет отклонение на значении 1536
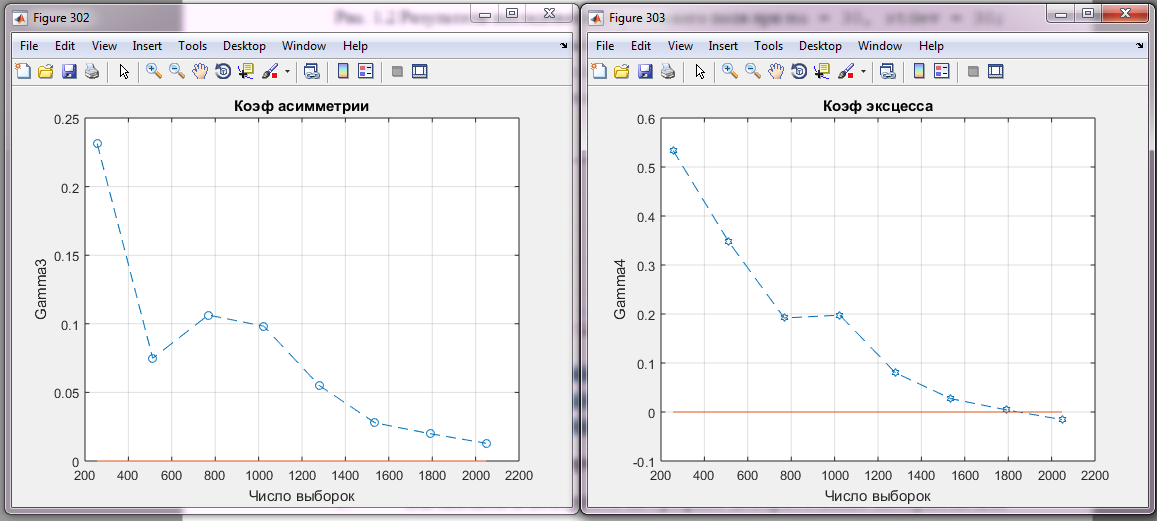
Рис 1.5 Зависимость выборочного коэффициента асимметрии от числа выборок
Так как выборочный коэффициент положительный, можно сделать вывод, что справа от центра имеются более тяжелые хвосты, чем слева. То есть распределение отклонено вправо.

Рис 1.6 Выборочный коэффициент эксцесса
Так как выборочный коэффициент эксцесса положительный, это указывает на то, что пик распределения более острый и более высокий, но с увеличением числа выборок пик распределения становится более пологий.
Далее в ходе исследования будут изменены значения параметров mu, stdev, и K
Mu=3
Stdev=30
К=1
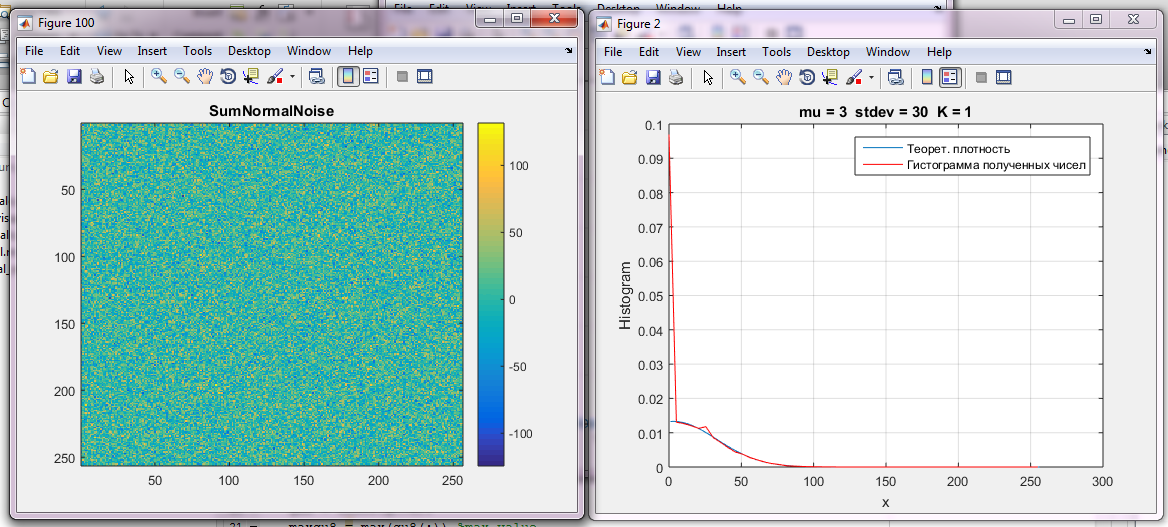
Рис 1.7 Суммарное гауссовское поле для mu = 3, stdev = 30; K = 1
Для человеческого глаза изменения не заметны

Рис 1.8 Гистограмма и плотность распределения
При сравнении гистограммы и плотности распределения заметны сильные изменения. График стал более плавным и отсутствуют резкие выбросы

Рис 1.9 Зависимость выборочного среднего от числа выборок
На графике видно, что выборочное среднее изменилось в 10 раз при изменении mu в 10 раз, соответственно поле сильно реагирует на изменение математического ожидания

Рис 1.10 Выборочная дисперсия
Выборочная дисперсия не изменилась при изменении mu в 10 раз.
Соответственно разброс значений параметра распределения гауссовского поля на основе выборки из данного поля не изменился после изменения мат ожидания, так как
выборочная дисперсия гауссовского поля может изменяться при изменении размера выборки или при изменении значений параметра распределения в гауссовском поле
Вывод:
Изучив гауссовское поле можно заключить, что изменение параметра математического ожидания влияет на центр распределения гауссовского поля, т. е. на его среднее значение. Сдвиг математического ожидания дает нам уменьшение всех значений в поле на 27 единиц (разность между двумя значениями mu). Это будет означать, что центр распределения теперь находится около нового значения Mu=3. Параметр стандартного отклонения, форма или
положение распределения не изменится, но может измениться ширина распределения. По итогу мат. Ожидание и кф. Корреляции изменяет гауссовское поле, но сохраняет свою форму и структуру.
Экспоненциальное поле
b- параметр масштаба поля
K- количество независимых реализаций поля
b = 30
K = 1
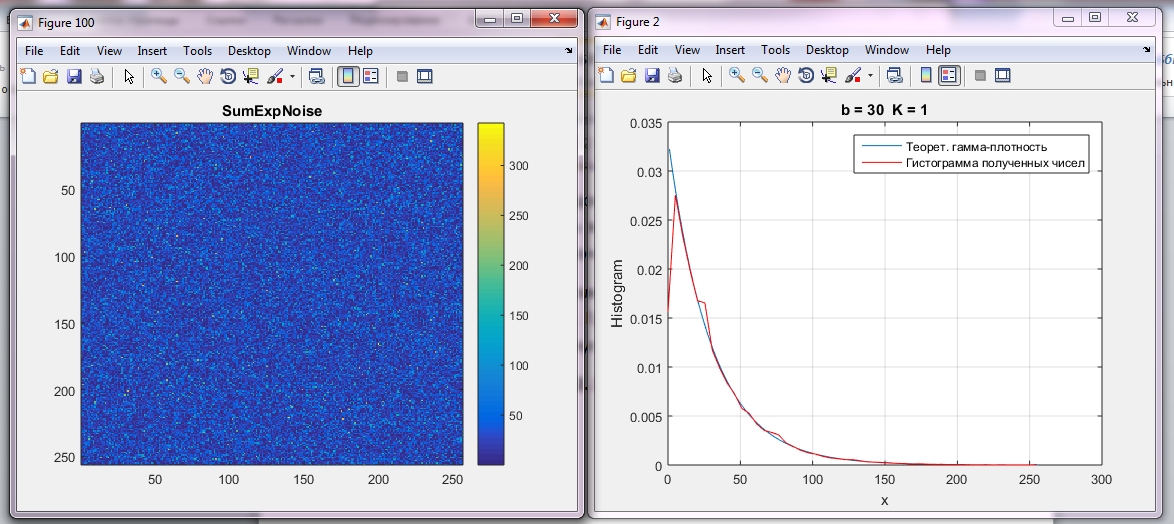
Рис. 2.1 Экспоненциальное поле

Рис 2.2 Гистограмма и плотность распределения
На графике видно, что гистограмма полученных чисел максимально приближена к теоретической гамма-плотности и имеет небольшое отклонение на значении 30.
Плотность распределения -это математическая функция, которая определяет вероятность того, что значение переменной попадет в определенный интервал.
Плотность распределения экспоненциального поля имеет форму экспоненциальной функции, которая начинается с высоких значений и убывает экспоненциально с ростом значения переменной x.
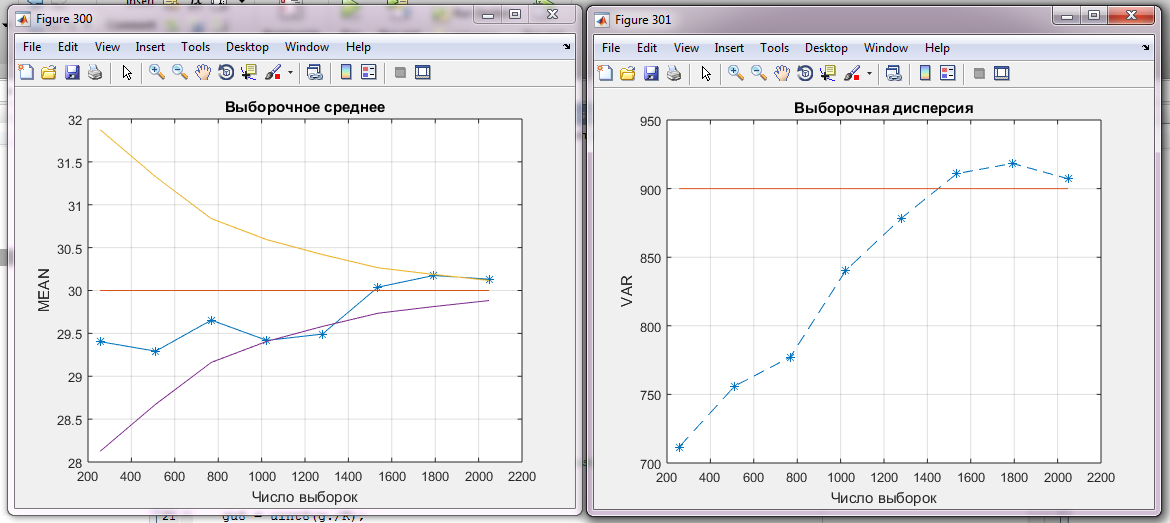
Рис. 2.3 Зависимость выборочного среднего от числа выборок
В случае экспоненциального распределения, математическое ожидание равно обратному значению параметра λ (среднего времени между двумя событиями). Таким образом, если мы берем достаточно большое число выборок из экспоненциального поля, то выборочное среднее будет приближаться к 1/λ.
На графике видно, что с увеличением количества выборок выборочное среднее приближается к теоретическим значениям параметров.

Рис 2.4 Выборочная дисперсия
Выборочная дисперсия экспоненциального поля зависит от объема выборки и неизвестного параметра λ экспоненциального распределения.
На графике мы видим, что с увеличением числа выборок выборочная дисперсия приближается к теоретическим значениям
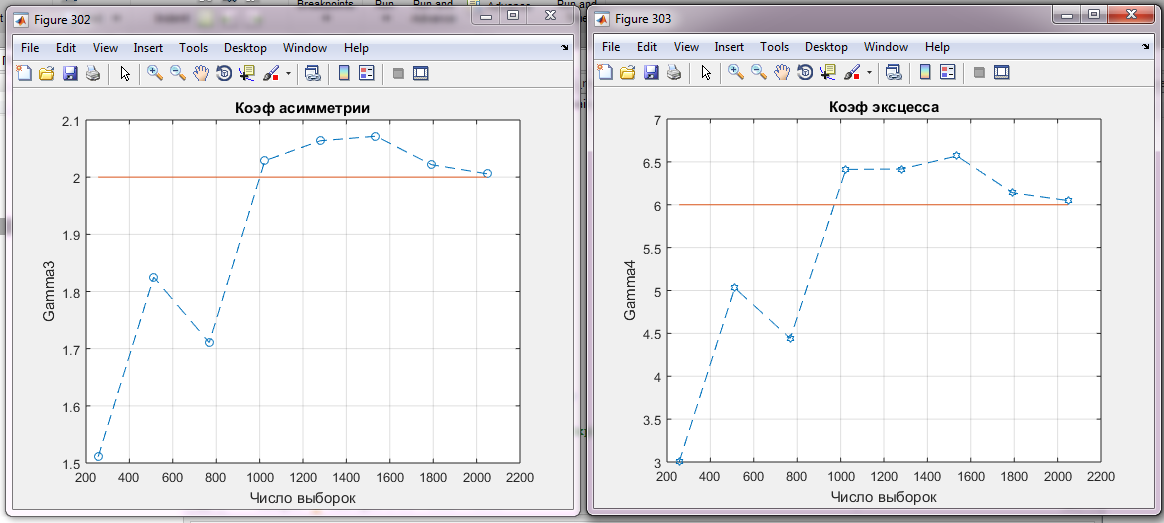
Рис. 2.5 Зависимость выборочного коэффициента асимметрии от числа выборок
Для экспоненциального поля коэффициент асимметрии равен 2, что означает его сильную положительную асимметрию. Коэффициент асимметрии является мерой симметрии распределения случайной величины и показывает, насколько сильно оно отклоняется от симметричного. В случае экспоненциального поля, которое является правоскошенным распределением, коэффициент асимметрии превышает 0 и говорит о том, что чаще встречаются значения больше среднего значения.

Рис 2.6 Выборочный коэффициент эксцесса
На графике видно, что пик распределения относительно ширины хвостов является острым
Далее в ходе исследования будут изменены значения параметра К на 6

Рис. 2.6 Экспоненциальное поле
При изменении К в 6 раз изменения экспоненциального поля оно стало заметно светлее

Рис. 2.7 Гистограмма и плотность распределения
На графике мы видим, что при изменении К=6 пик гистограммы сместился на значение 30, в отличие от К=1 и отсутствуют выбросы.
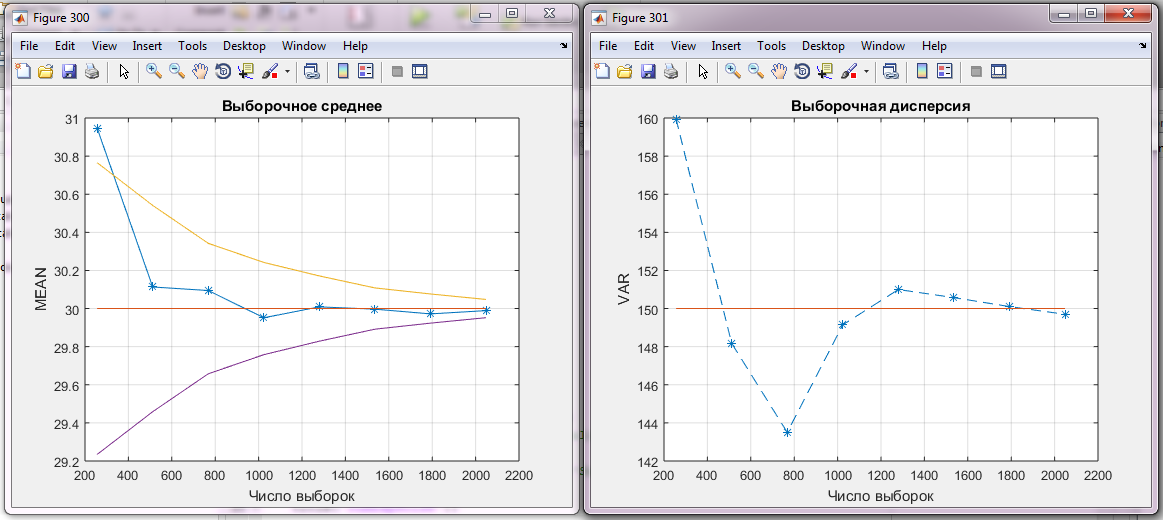
Рис 2.8 Зависимость выборочного среднего от числа выборок
На графике видно, что выборочное среднее при К=6 очень сильно отличается от значений при К=1. Соответственно при увеличении независимых реализаций поля значение 1/λ больше приближается к теоретическим значениям параметров.

Рис. 2.9 Выборочна дисперсия
На графике видно, что дисперсия осталась без изменений при К=6
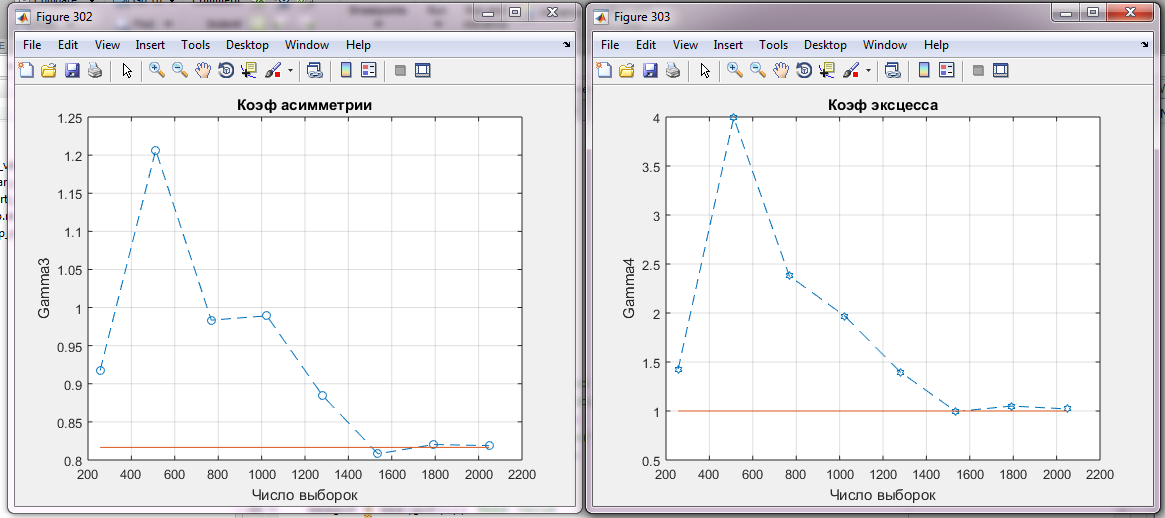
Рисунок 2.10 Зависимость выборочного коэффициента асимметрии от числа выборок
На графике видно, что теоретические значения параметров потерпели серьезные изменения с 2 при К=1 до 0,26 при К=6. Значения выборочного коэффициента асимметрии изменились в 2 раза, и график стал не повышающийся, а убывающий.

Рисунок 2.11 Выборочный коэффициент эксцесса
На графике видно, что при увеличении К до 6 пик распределения становится более пологим по сравнению с К=1
Поле с распределением Релея
Поле с распределением Рэлея - это случайный процесс, задающийся функцией распределения Рэлея. В этом распределении значение случайной величины X принимает значения от 0 до бесконечности и определяется следующей функцией распределения:
F(x) = 1 - exp(-x^2 / (2σ^2))
где σ - параметр масштаба.
Для поля с распределением Рэлея параметр масштаба должен быть задан для каждой точки в пространстве.