ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 444
Скачиваний: 32
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и молодежной политики Ставропольского края
Государственное бюджетное профессиональное образовательное учреждение
Георгиевский региональный колледж «Интеграл»
ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
По дисциплине « Математика: алгебра, начала математического анализа, геометрия»
На тему: “Графическое решение уравнений и неравенств”
Выполнил студент группы ПК-61, обучающийся по специальности
«Программирование в компьютерных системах»
Целлер Тимур Витальевич
Руководитель: преподаватель Серкова Н.А.
Дата сдачи: « » 2017г.
Дата защиты: « » 2017г.
Георгиевск 2017г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ЦЕЛЬ ПРОЕКТА:
Цель: Выяснить преимущества графического способа решения уравнений и неравенств.
Задачи:
-
Сравнить аналитический и графический способ решения уравнений и неравенств. -
Ознакомиться в каких случаях графический способ имеет преимущества. -
Рассмотреть решение уравнений с модулем и параметром.
Актуальность исследования: Анализ материала, посвящённого графическому решению уравнений и неравенств в учебных пособиях «Алгебра и начала математического анализа» разных авторов, учёт целей изучения данной темы. Атак же обязательных результатов обучения, связанных с рассматриваемой темой.
Содержание
Введение
1. Уравнения с параметрами
1.1. Определения
1.2. Алгоритм решения
1.3. Примеры
2. Неравенства с параметрами
2.1. Определения
2.2. Алгоритм решения
2.3. Примеры
3. Применение графиков в решении уравнений
3.1. Графическое решение квадратного уравнения
3.2. Системы уравнений
3.3. Тригонометрические уравнения
4. Применение графиков в решении неравенств
5.Заключение
6. Список литературы
Введение
Изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Некоторые Вузы также включают в экзаменационные билеты уравнения, неравенства и их системы, которые часто бывают весьма сложными и требующими нестандартного подхода к решению. В школе же этот один из наиболее трудных разделов школьного курса математики рассматривается только на немногочисленных факультативных занятиях.
Готовя данную работу, я ставил цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. На мой взгляд графический метод является удобным и быстрым способом решения уравнений и неравенств с параметрами.
В моём проекте рассмотрены часто встречающиеся типы уравнений, неравенств и их систем.
1. Уравнения с параметрами
-
Основные определения
Рассмотрим уравнение
(a, b, c, …, k, x)=(a, b, c, …, k, x), (1)
где a, b, c, …, k, x -переменные величины.
Любая система значений переменных
а = а0, b = b0, c = c0, …, k = k0, x = x0,
при которой и левая и правая части этого уравнения принимают действительные значения, называется системой допустимых значений переменных a, b, c, …, k, x. Пусть А – множество всех допустимых значений а, B – множество всех допустимых значений b, и т.д., Х – множество всех допустимых значений х, т.е. аА, bB, …, xX. Если у каждого из множеств A, B, C, …, K выбрать и зафиксировать соответственно по одному значению a, b, c, …, k и подставить их в уравнение (1), то получим уравнение относительно x, т.е. уравнение с одним неизвестным.
Переменные a, b, c, …, k, которые при решении уравнения считаются постоянными, называются параметрами, а само уравнение называется уравнением, содержащим параметры.
Параметры обозначаются первыми буквами латинского алфавита: a, b, c, d, …, k, l, m, n а неизвестные – буквами x, y,z.
Решить уравнение с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они.
Два уравнения, содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения является решением второго и наоборот.
-
Алгоритм решения
-
Находим область определения уравнения. -
Выражаем a как функцию от х. -
В системе координат хОа строим график функции а=(х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой а=с, где с(-;+) с графиком функции а=(х).Если прямая а=с пересекает график а=(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=(х) относительно х.
-
Записываем ответ.
-
Примеры
I. Решить уравнение
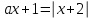 (1)
(1)Решение.
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :
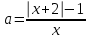
или
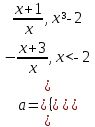
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.
Если а (-;-1](1;+)
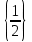 , то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения
, то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения 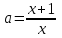 относительно х.
относительно х.Таким образом, на этом промежутке уравнение (1) имеет решение
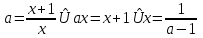 .
.Если а
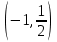 , то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений
, то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений 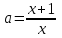 и
и 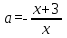 , получаем
, получаем 
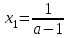 и
и 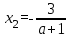 .
.Если а
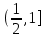 , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
, то прямая у=а не пересекает график уравнения (1), следовательно решений нет.Ответ:
Если а (-;-1](1;+)
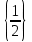 , то
, то 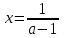 ;
;Если а
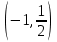 , то
, то 
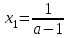 ,
, 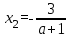 ;
;Если а
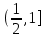 , то решений нет.
, то решений нет.II. Найти все значения параметра а, при которых уравнение
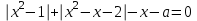 имеет три различных корня.
имеет три различных корня.Решение.
Переписав уравнение в виде
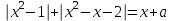 и рассмотрев пару функций
и рассмотрев пару функций 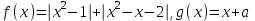 , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции
, можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции 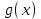
, при которых он имеет точно три точки пересечения с графиком функции
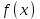 .
. В системе координат хОу построим график функции
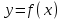 ). Для этого можно представить её в виде
). Для этого можно представить её в виде 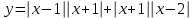 и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
и, рассмотрев четыре возникающих случая, запишем эту функцию в виде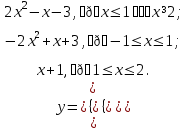
Поскольку график функции
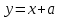 – это прямая, имеющая угол наклона к оси Ох, равный
– это прямая, имеющая угол наклона к оси Ох, равный 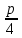 , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции
, и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции 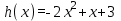 . Поэтому находим производную
. Поэтому находим производную 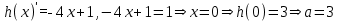
Ответ:
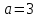 .
.III. Найти все значения параметра а, при каждом из которых система уравнений
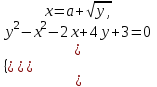
имеет решения.
Решение.
Из первого уравнения системы получим
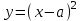 при
при 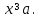 Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы
Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы 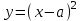 “скользят” вершинами по оси абсцисс.
“скользят” вершинами по оси абсцисс.Выделим в левой части второго уравнения полные квадраты и разложим её на множители
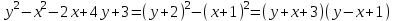
Множеством точек плоскости
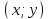 , удовлетворяющих второму уравнению, являются две прямые
, удовлетворяющих второму уравнению, являются две прямые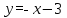 и
и 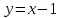
Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.
Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается
прямой
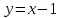
), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то
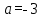 .
. Случай касания “полупараболы” с прямой
 определим из условия существования единственного решения системы
определим из условия существования единственного решения системы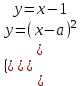
В этом случае уравнение
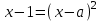
имеет один корень, откуда находим :
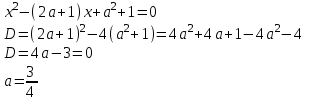
Следовательно, исходная система не имеет решений при
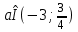 , а при
, а при 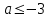 или
или 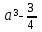 имеет хотя бы одно решение.
имеет хотя бы одно решение.Ответ: а (-;-3] (
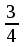 ;+).
;+).IV. Решить уравнение
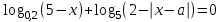
Решение.
Использовав равенство
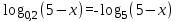 , заданное уравнение перепишем в виде
, заданное уравнение перепишем в виде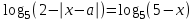
Это уравнение равносильно системе
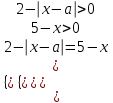
Уравнение
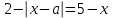 перепишем в виде
перепишем в виде 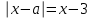 . (*)
. (*) Последнее уравнение проще всего решить, используя геометрические соображения. Построим графики функций
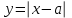 и
и 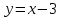 Из графика следует, что при
Из графика следует, что при 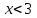 графики не пересекаются и, следовательно, уравнение не имеет решений.
графики не пересекаются и, следовательно, уравнение не имеет решений.Если
 , то при
, то при 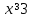 графики функций совпадают и, следовательно, все значения
графики функций совпадают и, следовательно, все значения 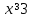 являются решениями уравнения (*).
являются решениями уравнения (*).При
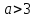 графики пересекаются в одной точке, абсцисса которой
графики пересекаются в одной точке, абсцисса которой