ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 31
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования Республики Беларусь
Учреждение образования
«Могилевский государственный университет продовольствия»
Кафедра прикладной механики и инженерной графики
Расчёт вала на выносливость
Расчетно-графическая работа № 2
Вариант 2.6
по дисциплине «Прикладная механика»
Специальность 1-49 01 01 Технология хранения и переработки пищевого и растительного сырья
Специализация 1-49 01 01 02 Технология хлебопекарного, макаронного, кондитерского производств и пищеконцентратов
| Проверил | Выполнила |
| ст. преподаватель | студентка группы ТРХ-141 |
| ________________А.В.Евдокимов | ____________А.В.Удовенко |
| «___ »________________2016 г. | «___ »_______________2016 г. |
Могилев 2016
Содержание
-
Условие задачи 3 -
Решение 4-
Проектный расчет вала 4 -
Проверочный расчет на выносливость 7 -
Расчет шпоночного соединения 9 -
Расчет и подбор подшипников качения 9
-
Список использованных источников 11
1. Условие задачи
По заданным геометрическим параметрам вала, крутящему моменту, размере зубчатых колес требуется выполнить:
-
Расчет промежуточного вала двухступенчатого редуктора на усталостную прочность. -
Рассчитать шпоночные соединения в месте посадки зубчатых колес. -
Подобрать и рассчитать на динамическую грузоподъемность подшипники качения.
Направление сил на вал определять расположением сопряженных зубчатых колес, показанных на рисунке тонкими линиями.
Расчет на выносливость выполнять по номинальной нагрузке указанной в таблице. А цикл напряжений принять симметричным для напряжения изгиба и пульсационным для напряжения кручения.
Расчет шпоночного соединения провести по напряжению среза и смятия. Подшипники качения проверить на динамическую грузоподъемность. Для расчета принять
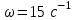
, долговечность подшипников Lh=15000 ч.
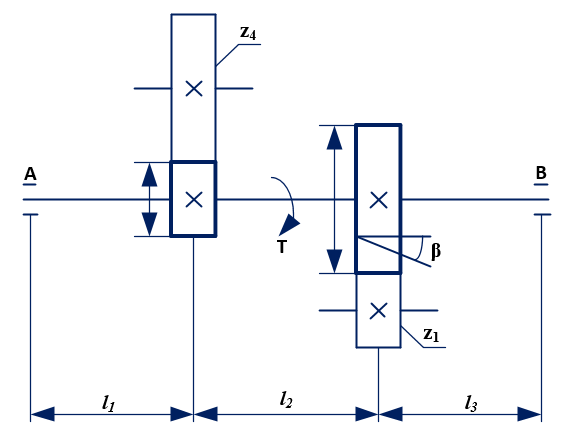
Рисунок 1 – Схема вала
Дано:T=250 Н
м ; d2=150 мм ; d3=50 мм ; l1=70 мм ; l2=50 мм ; l3=45 мм ; β=12 град ; ω=15
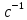; Lh=15000 часов.2. Решение
2.1 Проектный расчёт вала
Определяем силы, возникающие в зацеплении:
Передача 1-2 цилиндрическая косозубая.
Окружная сила
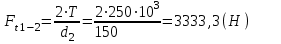(1) Осевая сила
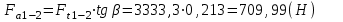(2)Радиальная сила
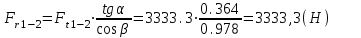(3)Передача 4-3 цилиндрическая прямозубая.
Окружная сила
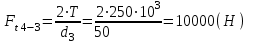(4)Осевая сила
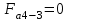
так как
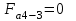,то изгибающий момент = 0 Радиальная сила
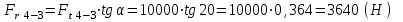(5)Строим схему нагружения в вертикальной плоскости и составляем уравнения равновесия относительно точек А и B:
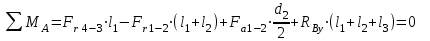
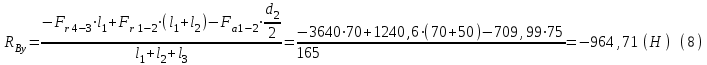
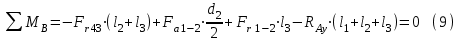
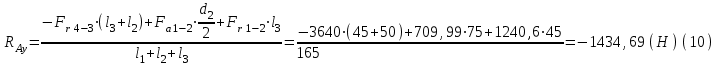
Проверка:
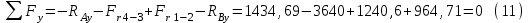
Строим эпюру изгибающих моментов в вертикальной плоскости.
Тогда согласно правилу знаков:
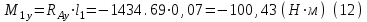
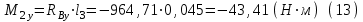
Строим схему нагружения в горизонтальной плоскости и составляем уравнения равновесия относительно точек А и B:
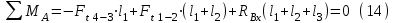
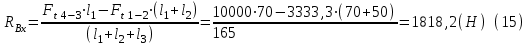
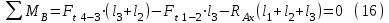
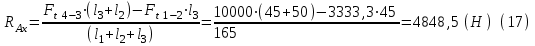
Проверка
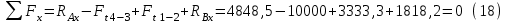
Cтроим эпюры изгибающих моментов в горизонтальной плоскости. Рассмотрим участок длиной l1 на этом участке действует только сила RAx. Тогда:
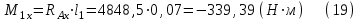
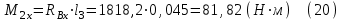
Строим суммарную эпюру изгибающего момента
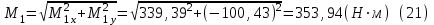
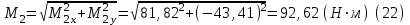
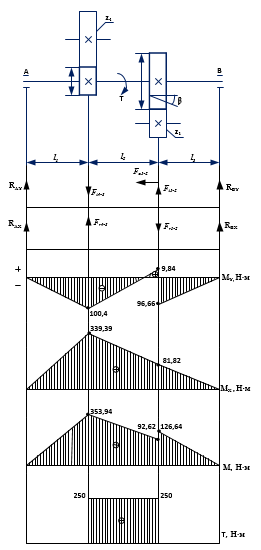
Рисунок 2 – Эпюры к решению задачи
Максимальный изгибающий момент Мmax=298 (Н
м) под шестерней 3. Определяем диаметр вала в месте посадки зубчатых колес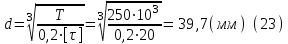
где [τ] – пониженное допускаемое напряжение при кручении [τ]=10-20 МПа.
Принимаем диаметр вала под подшипники: dп=40 мм.
Принимаем диаметр вала в месте посадки d=35мм
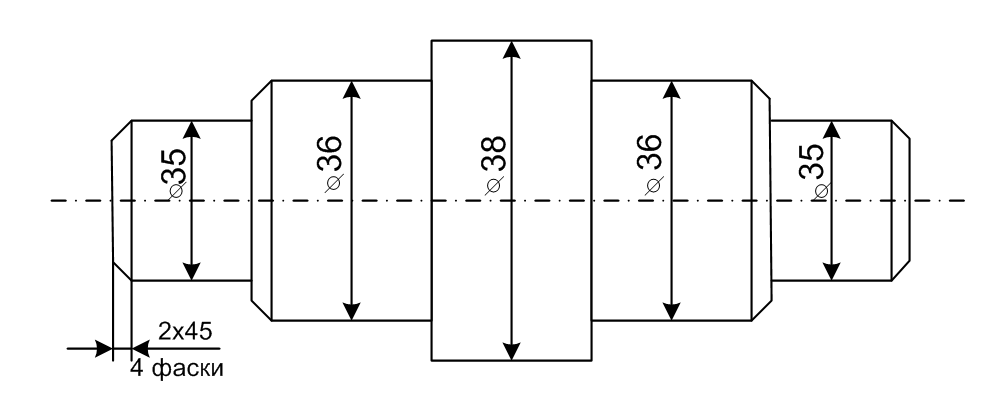
Рисунок 3 – Эскиз вала
2.2 Проверочный расчет на выносливость
Опасным сечением вала является сечение под колесом 3. Запишем условие прочности
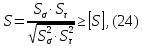
где S – расчетный коэффициент запаса прочности;
[S] – требуемый коэффициент для запаса прочности и жесткости (при совместном действии напряжений кручения и изгиба [S] ≈ 1,5); [2]
Sσ – коэффициент запаса прочности по нормальным напряжениям;
Sτ – коэффициент запаса прочности по касательным напряжениям.
Принимаем материал вала Сталь 45 с пределом прочности σпч = 610 МПа. [2]
Предел выносливости материала вала при симметричных циклах изгиба
, 
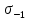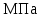и кручения 
,
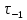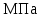
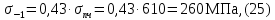
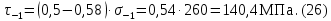
Так как по условию задано, что нормальные напряжения, возникающие в поперечном сечении вала от изгиба, изменяются по симметричному циклу, то среднее напряжение цикла нормальных напряжений σm = 0, а его амплитуда
, 
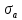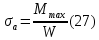
где W – момент сопротивления сечения,
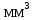.Для сечения ослабленного шпоночной пазом
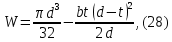
где b = 12 мм – ширина шпонки при d = 40 мм; [1]
t = 5 мм – глубина шпоночного паза при d = 40 мм. [1]
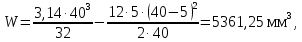
Согласно условию цикл касательных напряжений является пульсационным
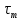, тогда амплитуда и среднее значение цикла касательных напряжений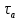 
, 
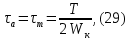
где
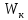- момент сопротивления сечения при кручении, .
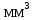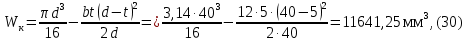
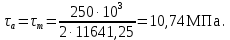
Коэффициент запаса прочности по нормальным
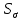и касательным 
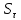напряжениям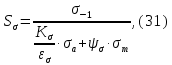
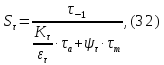
где Кσ и Кτ – эффективные коэффициенты концентрации напряжений при изгибе и кручении (для сталей с σпч ≤ 700 МПа и сечений, ослабленных шпоночной канавкой
Кσ = 1,75, Кτ = 1,5 [1]);
εσ и ετ – масштабные факторы для нормальных и касательных напряжений (при изгибе углеродистой стали и кручении для всех сталей при d = 36 мм εσ = 0,862, ετ = 0,746 [1]);
ψσ и ψτ – коэффициенты, учитывающие влияние постоянной составляющей цикла на выносливость (для среднеуглеродистых сталей ψσ = 0,2, ψτ = 0,1 [1]).
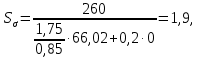
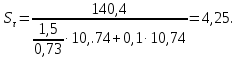
Тогда расчетный коэффициент запаса прочности
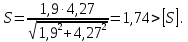
Таким образом, прочность и жесткость вала обеспечены.
2.3 Расчет шпоночного соединения
По условию задачи расчет шпоночных соединений необходимо произвести по напряжениям смятия и среза.
При d = 36 мм определяем ширину шпонки b = 10 мм, глубину шпоночной канавки t = 5 мм и высоту шпонки h = 8 мм. [1]
Рабочую длину шпонки lр определим из условия прочности на смятие
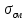, МПа, которое имеет вид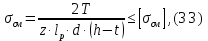
где z – число шпонок (принимаем z = 1); [1]
[σсм] – допускаемое напряжение при смятии (при расчетах можно принять [σсм] = 60 – 100 МПа). [1]
Приравнивая расчетные напряжения к допускаемым и выражая рабочую длину шпонки, имеем
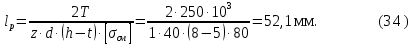
Проверяем условие прочности на срез
, 
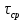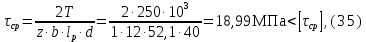
где [τср] - допускаемые напряжения на срез [τср] = 100 МПа.
Так как условие прочности выполняется, то полная длина шпонки
, 
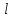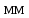
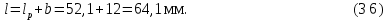
Окончательно принимаем к установке шпонку 12×8×70 по ГОСТ 23360 – 78. [1]
2.4 Расчет и подбор подшипников качения
Определим реакции в опорах А и В: