Лабораторная работаИзмерение ускорения силы тяжести с помощью математического маятникаЦель работы: Измерение ускорения силы тяжести с помощью математического маятника. Обработка результатов измерения.Приборы, принадлежности:

1. 
   Математический маятника
   
2. 
   Секундомер
   

Краткая теория

1. 
   Материальная точка, подвешенная на гибкой, невесомой и нерастяжимой нити, называется математическим маятником. Близким к математическому маятнику является тяжелый шарик, подвешенный на длинной тонкой нити. Вес такой материальной точки P = mg. В вертикальном положении сила тяжести P материальной точки полностью уравновешивается натяжением нити, и маятник остается в покое (положение равновесия)
   

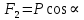
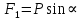
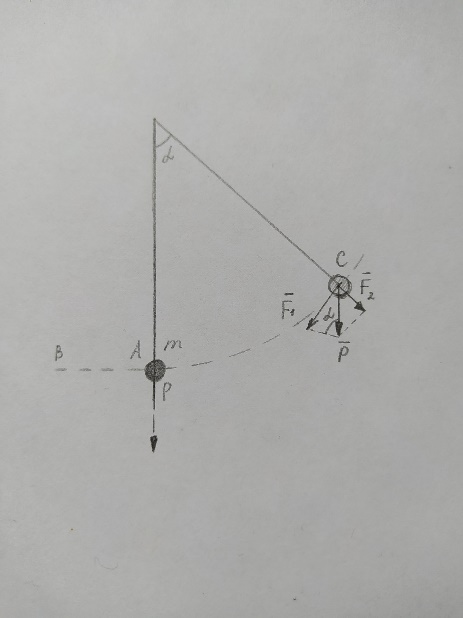
Если маятник отклонить от положения равновесия на некоторый угол α, то составляющая силы тяжести, Направленная вдоль нити, или сила Уравновесится натяжением нити, другая Составляющая – силаПерпендикулярная к нити, стремится вернуть Маятник в положении равновесия.Длина дуги АС, на которую маятник отклонился от положения равновесия, называется смещением. Если смещение от А к С считать положительным, а от А к В – отрицательным, то сила 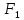всегда будет направленна обратно смещению и при малых углах уклонения ( 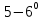) пропорционально смещению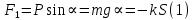Где S – смещение (длина дуги АС)k – коэффициент пропорциональностиВ общем случае колебания математического маятника не являются гармоническими, их период T зависит от амплитуды. 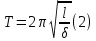Но если отклонения малы, он совершает колебания, близкие к гармоническим с периодомВ этом случае период Т не зависит от амплитуды

---

, т.е. колебания изохронны.


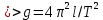
Где l = OA = OC – длина математического маятника

g – ускорение силы тяжести.

Из формулы (2) следует, что период колебания математического маятника не зависит от амплитуды колебания (от начального угла отклонения, если угол 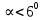) и от массы маятника, а определяется отношением длины его к ускорению силы тяжести.

Следовательно, измерив период колебания математического маятника данной длины, мы можем определить величину ускорения силы тяжести

2. 
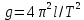
   Метод измерения. Длинной маятника l следует считать расстояние от точки подвеса О до центра тяжести шарика.
   

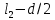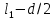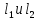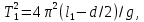
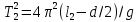
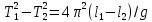
Но подводя подвижную линейку касательной к нижнему краю шарика, мы измеряем l + d/2, где d – диаметр шарика, поэтому измерение будет ближе к идеальному (маятник – материальная точка), если ввести в расчет периоды колебаний маятников двух различных длин: и , где – результат измерения, проведенного с помощью подвижной линейки. В этом случае получаем:Вычитая из первого выражения второе, получим:Откуда (4)Таким образом, для определения g по формуле (4) необходимо измерить лишь разностью ( 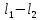) . При таком способе измерения исключается необходимость измерения диаметра шарика, а следовательно, определение ускорения будет точнее.Порядок выполнения работы.

1. 
   Установить большую длину маятника, опустив для этого шарик как можно ниже.
   
2. 
   Подводя подвижную горизонтальную линейку касательно к нижнему краю шарика, отметить число делений по шкале вертикальной стойки и миллиметровой шкале, это соответствует .
   
3. 
   Отводят маятник от положения равновесия на небольшой угол (порядка 5-6), опускают шарик, предоставив ему свободно колебаться. В какой – либо момент наибольшего отклонения маятника пускают в ход секундомер и отсчитывают время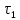 , в течение которого маятник совершает n = 50 полных колебаний. Измерение времени 50 колебаний для неизменной длины проводится три раза, результат записывают в таблицу.
   
4. 
   Устанавливают новую длину маятника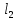 , снова отмечают положение горизонтальной линейки, подведенной касательной к нижнему краю шарика, что соответствует длине .
   
5. 
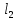   Аналогично пункту «3» измеряют время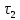 . Измерение времени .
   
6. 
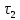   Результаты заносятся в таблицу.
   

---

№
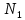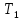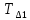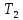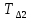1	1,20	15	31,43	2,09	0,07	0,95	28,42	1,89	0,02
2	1,20	15	33,20	2,21	0,05	0,95	28,09	1,87	0,01
3	1,20	15	32,54	2,17	0,01	0,95	28,24	1,88	0,01
4	1,20	15	32,24	2,15	0,01	0,95	27,62	1,84	0,03
5	1,20	15	32,02	2,17	0,01	0,95	28,02	1,86	0,01
Ср.знач				2,15				1,87

7. 
   По результатам измерений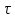 времени полных колебаний рассчитывают периоды колебани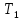й и 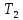по формуле.
   

---

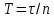
n – число полных колебаний, – время полных колебаний

8. 
   Вычисляют g, пользуясь формулой (4)
   

9. 
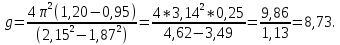
   Вычисляют погрешность.
   

Вывод

Измерены ускорения силы тяжести с помощью математического маятника. Обработаны результаты измерения.

---

Смотрите также файлы

• Теоретические основы бюджетного устройства и бюджетной системы российской федерации 3.docx

• Учебная задача (математика, 5 класс).docx

• Отчет по производственной рассредоточенной практике (вид практики) в.docx

• Занятие по химии viiй группы элементов Заключение.doc

• Интерфейс периферийных устройств pci. Pciexpress.doc