ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 39
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Последовательности, их общий вид, способы задания.
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Xn – общий член последовательности
Последовательность можно задать несколькими способами:
- Аналитически или, проще говоря, формулой.
- Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
- Описательно, простым перечислением всех элементов последовательности.
Арифметическая и геометрическая прогрессии, их общий член и частичные суммы.
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.
Сумма первых n членов прогрессии вычисляется по формуле:
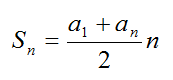
Геометрическая прогрессия – это такая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число q – знаменатель прогрессии.
Сумма первых n членов прогрессии:
-
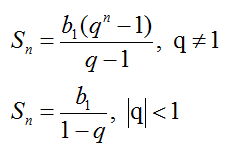
Предел последовательности.
Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.
Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.
Переменная n в последовательностях всегда стремится к бесконечности
, в сторону увеличения натуральных чисел.
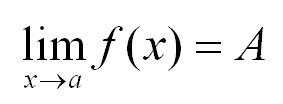
Бесконечно малые и бесконечно большие величины, ограниченные последовательности.
Бесконечно малая — числовая последовательность, предел которой равен нулю.
limαn=0
n→∞
Бесконечно большая — числовая последовательность, стремящаяся (равна) к бесконечности определённого знака.
lim xn=∞
n→∞
-
Теоремы о единственности предела, о предельном переходе в неравенствах, о сжатой переменной.
Теорема о единственности предела: последовательность, не может одновременно стремиться к двум различным пределам, то есть если предел последовательности существует, то он единственный.
Теорема о предельном переходе в неравенствах: если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).
Теорема о сжатой переменной:
Пусть даны три последовательности
, 
и 
, причем 
. Пусть последовательности и имеют один и тот же предел а: 
. Тогда последовательность
так-е имеет предел а: 
Пусть даны
последовательности и существует : 
: 
, 
. Известно, что 
. Тогда 
.Связь с ограниченностью.
Если последовательность имеет конечный предел, то она является ограниченной.
-
Пределы суммы, разности, произведения, частного и степени.
1) Предел суммы двух функций равен сумме их пределов:
2) Предел разности равен разности пределов
3) Предел произведения двух функций равен произведению их пределов:
.4)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:
.5) Предел степени переменной равен той же степени предела основания
Внесем знак предела внутрь скобок, а степень останется при этом снаружи.
Лемма о произведении бесконечно малой на ограниченную.
Произведение бесконечно малой функции
при
на ограниченную функцию
есть бесконечно малая функция.
Теорема о монотонной ограниченной последовательности Вейерштрасса.
-
Иррациональная степень, элементарные функции.
Пусть
– иррациональное число, а 
.Степенью числа
с иррациональным показателем называется действительное число 
, такое что для любых 
, таких что 
выполняется неравенство 
, если 
, и 
, если 
. Если же 
, то полагаем 
.Обозначение:
.
Предел функции.
Определения разных пределов.
Пределы суммы, разности, произведения, частного и степени.
-
Замечательные пределы.
обозначения двух математических тождеств со взятием предела:
О маленькое.
, «о малое от
» обозначает «бесконечно малое относительно »[1], пренебрежимо малую величину при рассмотрении -
Непрерывность.
Непрерывность суммы, разности, произведения и частного.
Непрерывность сложной функции.
Непрерывность обратной функции.
Непрерывность элементарных функций. -
Теоремы Больцано-Коши и Вейерштрасса.
Использование непрерывности для вычисления пределов. -
Ряды.
Примеры геометрической прогрессии, гармонического ряда.
Сходящиеся и расходящиеся ряды.
Свойства: предел общего члена, умножение на число, сумма/разность, объединение членов. -
Положительные ряды: сравнение двух рядов, признаки Даламбера и Коши, отношение положительных рядов. -
Положительные ряды: переместительное свойство, произведение рядов. Знакочередующиеся ряды, признак Лейбница. -
Абсолютно сходящиеся ряды: определение с примерами, теорема, переместительное свойство, произведение рядов, оценка суммы и видоизмененный признак Даламбера. -
Производная. Определение и примеры, геометрический смысл.
Дифференцируемость и непрерывность.
Производные простейших элементарных функций.
Производная суммы, разности, произведения и частного. -
Производная обратной функции.
Производная сложной функции.
Производная f(x)g(x) и logf(x)g(x).
Таблица производных.
Производная параметрически заданной функции. -
Теоремы Ферма, Ролля, Лагранжа и Коши. -
Дифференциал функции.
Правило Лопиталя.
Формула Тейлора (напомнить про факториалы). -
Первообразная и неопределенный интеграл.
Свойства неопределенных интегралов.
Таблица основных интегралов. -
Неопределенный интеграл.
Метод подстановки (в обе стороны).
Метод интегрирования по частям.
Интегрирование рациональных функций (в общих чертах). -
Определенный интеграл. Определение.
Достаточное условие интегрируемости.
Свойства определенного интеграла. -
Функция верхнего предела.
Формула Ньютона-Лейбница.
Замена переменных.
Интегрирование по частям. -
Примеры вычисления площади круга, объемов шара и конуса.