Файл: Тменгі Пенжім орта мектебі мдшо кмм (білім беру йымыны атауы).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 35
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
«Төменгі Пенжім орта мектебі мдшо» кмм
(білім беру ұйымының атауы)
Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттер
(сабақтың тақырыбы)
| Бөлім: | Алғашқы функция және интеграл | ||
| Педагогтің аты-жөні: | Аширов Б. Я. | Тексерілді: | |
| Күні: | 13.09.2022 | ||
| Сынып: 11 «Ә» | Қатысушылар саны: | Қатыспағандар саны: | |
| Сабақтың тақырыбы | Алғашқы функция және анықталмаған интеграл. Анықталмаған интеграл қасиеттер | ||
| Оқу бағдарламасына сәйкес оқыту мақсаттары | 11.3.1.1 - алғашқы функция және анықталмаған интеграл анықтамаларын білу; 11.3.1.2 - анықталмаған интеграл қасиеттерін білу және қолдану; | ||
| Сабақтың мақсаты | Алғашқы функция туралы негізгі ұғымдарды түсіндіру ,есептер шығаруда формулаларды дұрыс пайдалануды үйрету | ||
Сабақтың барысы
| Сабақтың кезеңі/ уақыт | Педагогтің әрекеті | Оқушының әрекеті | Бағалау | Ресурстар |
| Сабақ басы 3 минут | Сәлемдесу. Оқушылардың сабаққа дайындығын тексеру. Оқушылармен бірге сабақтың мақсаттарын және күтілетін нәтижелерді анықтаймыз. | Оқушылар сұрақтарға жауап береді | Сұрақтарға жауап берегніне қарай бағалау | |
| Сабақтың ортасы 25 | Анықтама: Егер берілген аралықта F′(х) = (х) теңдігі орындалатын болса, онда осы аралықта F(х) функциясын (х) функциясы үшін алғашқы функция деп атайды. 1- мысал: (х) =3х2, хR функциясы үшін алғашқы функция F(x)=x3 болады, себебі F' (x)= 3х2 = (х) әрбір хR функциясы үшін. 2- мысал: F (x)= х3 / 3 функциясы F (x)= х2 функция үшін (- ; ) интервалында алғашқы функция болады , өйткені барлық х (- ; ) үшін F' (x)= ( х3 / 3 )' = 1 / 3 (х3) ' =1 / 3 ∙ 3х2 = x2 = (х). 2. Алғашқы функцияның негізгі қасиеті Белгілі бір I аралықта (х) функциясы үшін алғашқы функциялардың кез-келгенін мына түрде жазып көрсетуге болады, F (x) + С (1) мұндағы С - кез-келген тұрақты шама, ал F(x)+С I аралығында (х) функциясы үшін алғашқы функция болып табылады. егер у = x2, онда у' = 2x егер у = x2 +84, онда у'=2x егер у = x2-15, онда у'=2x 3. Алғашқы функцияны табудың үш ережесі Бұл ережелер дифференциалдаудың сәйкес ережелеріне ұқсас. 1 – ереже. Егер үшін алғашқы функция F, ал g үшін алғашқы функция G болса , + g үшін алғашқы функция F + G болады . Шынында да, F = және G = g болатындықтан, қосындының туындысын есептеу ережесі бойынша: (F + G) = F + G = + g 2 – ереже. Егер үшін алғашқы функция F, ал k – тұрақты шама болса , онда k үшін алғашқы функция k F болады . Шынында да, тұрақты көбейткішті туынды таңбасының алдына шығаруға болады, сондықтан (kF) = kF = k 3 – ереже. Егер F(x) функциясы (x) үшін алғашқы функция, ал k мен b – тұрақты шамалар болып , k 0 болса , онда (kx + b) функциясы үшін алғашқы функция 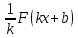 болады. болады. | . | | |
| Сабақтың соңы 14 минут | Анықталмаған интеграл дегеніміз не? Анықтама: Берілген аралықтағы (х) функциясының алғашқы функциясы осы аралықтағы (х) функциясының анықталмаған интегралы деп аталады. Белгіленуі: (х) dx (икстен эф де икс функциясының анықталмаған интегралы деп оқылады) Анықтамаға сәйкес: (х)dx=F(x)+C Мұндағы: – интеграл таңбасы (х) – интеграл астындағы функция (х) dx – интеграл астындағы өрнек х – интегралдау айнымалысы C – кез-келген тұрақты шама | Берілген есептерді шығарады | Есептерді шығарғанына байланысты, оқушылардың білімін балл бойынша бағалау | |
| Кері байланыс 3 минут | “Бүгінгі сабақта тақырыбы…” “Мен сабақта жаңа терминдермен ...........таныстым....” | | | |