Ф. Имя ___________________________________________

№	Задания	Ответы
1	Медиана равностороннего треугольника равна 11√3. Найдите сторону этого треугольника.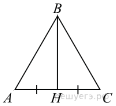
2	Найдите ве­ли­чи­ну (в градусах) впи­сан­но­го угла α, опи­ра­ю­ще­го­ся на хорду  AB, рав­ную ра­ди­у­су окружности.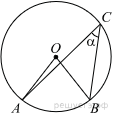
3	Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ражённого на ри­сун­ке.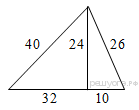
4	Най­ди­те тангенс угла А тре­уголь­ни­ка ABC, изображённого на рисунке.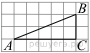
5	Какие из следующих утверждений верны?   1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны. 2) Любые две прямые имеют не менее одной общей точки. 3) Через любую точку проходит более одной прямой. 4) Любые три прямые имеют не менее одной общей точки.   Если утвер­жде­ний несколько, за­пи­ши­те их номера в по­ряд­ке возрастания.

Ответы:

1. 
   22
   
2. 
   30
   
3. 
   504
   
4. 
   0,4
   
5. 
   13
   

Решение:

1. Так как треугольник АВС равносторонний, то его медиана ВН является и биссектрисой, и высотой. Тогда треугольник АВН - прямоугольный. Тогда:



Ответ:22

2. Проведем радиусы OA и OB. Так как по условию задачи хорда AB равна радиусу, то треугольник AOB — равносторонний, следовательно, все его углы равны 60°. Угол 

---

AOB — центральный и равен 60° Угол ACB — вписанный и опирается на ту же дугу, что и угол AOB. Таким образом, 

 

Ответ: 30

3. Заметим, что треугольник со сторонами 24, 32 и 40 подобен египетскому треугольнику со сторонами 3, 4, 5 с коэффициентом 8. Следовательно, этот треугольник прямоугольный, а отрезок длины 24 — высота изображенного на рисунке треугольника. Тогда его площадь можно найти как половину произведения основания на высоту:

 



Ответ: 504

4. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:

 



Ответ: 0,4.

5. Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.» — верно, так как если соответственные углы равны, то прямые параллельны.

2) «Любые две прямые имеют не менее одной общей точки.» — неверно, две прямые имеют не более одной общей точки.

3) «Через любую точку проходит более одной прямой.» — верно, через одну точку проходит множество пересекающихся в этой точке прямых.

4) «Любые три прямые имеют не менее одной общей точки.» — неверно, любые три прямые, которые не совпадают, если и имеют общую точку, то только одну.

 

Ответ: 13.

---

Смотрите также файлы

• Депозиты и домашние кредиты.docx

• Тема 11. Гражданское право России в xix нач. Xx вв. Систематизация Российского законодательства в xix в.docx

• Отчет о лабораторной работе 1.docx

• Практические задания Работа с регистром символов.docx

• Построение сетевого графика ремонта колесных пар. Оптимизация сетевого графика по времени и трудовым ресурсам.doc