Файл: Энтропия как мера степени неопределенности системы.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 37

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»

Институт информатики и телекоммуникаций
Кафедра информационно-управляющих систем
Отчет по лабораторной работе №1


Тема: Энтропия как мера степени неопределенности системы




Преподаватель _________Курашкин С.О.
Обучающийся БИЭ21-01 211211015 ____________Навицкая А.А.

Красноярск 2023

Цель работы: Закрепить теоретические знания и получить практические навыки при вычислении энтропии.
Задание:

1. Получить таблицу значений функции 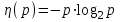при изменении р от 0,01 до 0,99 с шагом 0,01.

2. Система может находиться в двух состояниях. Вероятность одного состояния p. Определить значения энтропии при изменении p от 0,01 до 0,99 с шагом 0,01. Определить максимальное значение энтропии. Построить график.

3. Пользуясь таблицей частот русского языка (таб. 2) определить энтропию однобуквенного сочетания русского текста.
Решение

Задание №1: Получить таблицу значений функции 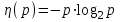при изменении р от 0.01 до 0.99 с шагом 0.01


p
n(p)

0,01
0,06643856

0,02
0,11287712

0,03
0,15176681

0,04
0,18575425

0,05
0,2160964

0,06
0,24353362

0,07
0,26855509

0,08
0,2915085

0,09
0,31265381

0,1
0,33219281

0,11
0,3502867

0,12
0,36706724

0,13
0,38264414

0,14
0,39711018

0,15
0,41054484

0,16
0,42301699

0,17
0,43458687

0,18
0,44530761

0,19
0,45522645

0,2
0,46438562

0,21
0,47282314

0,22
0,48057341

0,23
0,48766767

0,24
0,49413449

0,25
0,5

0,26
0,50528828

0,27
0,51002155

0,28
0,51422035

0,29
0,51790381

0,3
0,52108968

0,31
0,52379456

0,32
0,52603398

0,33
0,52782248

0,34
0,52917374

0,35
0,53010061

0,36
0,53061523

0,37
0,53072904

0,38
0,5304529

0,39
0,52979705

0,4
0,52877124

0,41
0,52738472

0,42
0,52564628

0,43
0,52356432

0,44
0,52114681

0,45
0,51840139

0,46
0,51533535

0,47
0,51195565

0,48
0,50826897

0,49
0,50428171

0,5
0,5

0,51
0,49542973

0,52
0,49057657

0,53
0,48544594

0,54
0,48004309

0,55
0,47437306

0,56
0,46844071

0,57
0,46225072

0,58
0,45580761

0,59
0,44911575

0,6
0,44217936

0,61
0,4350025

0,62
0,42758913

0,63
0,41994305

0,64
0,41206796

0,65
0,40396744

0,66
0,39564497

0,67
0,38710389

0,68
0,37834748

0,69
0,3693789

0,7
0,36020122

0,71
0,35081744

0,72
0,34123046

0,73
0,33144309

0,74
0,32145809

0,75
0,31127812

0,76
0,30090579

0,77
0,29034363

0,78
0,2795941

0,79
0,2686596

0,8
0,25754248

0,81
0,24624501

0,82
0,23476943

0,83
0,22311791

0,84
0,21129256

0,85
0,19929547

0,86
0,18712863

0,87
0,17479404

0,88
0,16229362

0,89
0,14962926

0,9
0,13680278

0,91
0,12381601

0,92
0,1106707

0,93
0,09736856

0,94
0,0839113

0,95
0,07030055

0,96
0,05653794

0,97
0,04262505

0,98
0,02856342

0,99
0,01435457




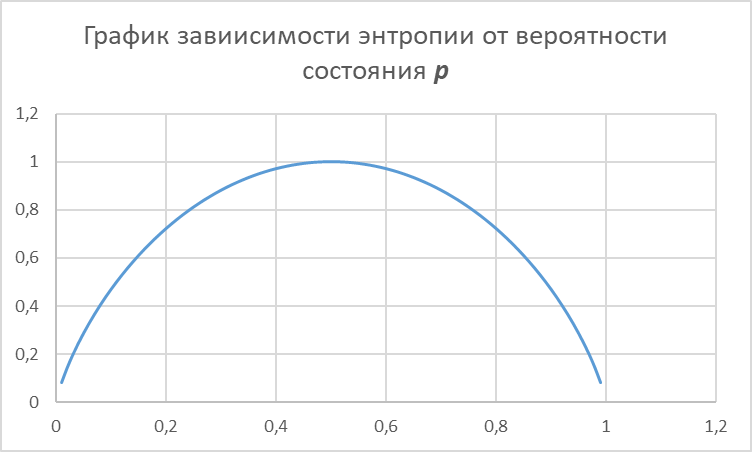
Задание 2: Система может находиться в двух состояниях. Вероятность одного состояния Р. Определить значения энтропии при изменении Р от 0,01 до 0,99 с шагом 0,01. Определить максимальное значение энтропии. Построить график.



x1
x2
H(x)

p
1-p

0,01
0,99
0,0808

0,02
0,98
0,1414

0,03
0,97
0,1944

0,04
0,96
0,2423

0,05
0,95
0,2864

0,06
0,94
0,3274

0,07
0,93
0,3659

0,08
0,92
0,4022

0,09
0,91
0,4365

0,1
0,9
0,4690

0,11
0,89
0,4999

0,12
0,88
0,5294

0,13
0,87
0,5574

0,14
0,86
0,5842

0,15
0,85
0,6098

0,16
0,84
0,6343

0,17
0,83
0,6577

0,18
0,82
0,6801

0,19
0,81
0,7015

0,2
0,8
0,7219

0,21
0,79
0,7415

0,22
0,78
0,7602

0,23
0,77
0,7780

0,24
0,76
0,7950

0,25
0,75
0,8113

0,26
0,74
0,8267

0,27
0,73
0,8415

0,28
0,72
0,8555

0,29
0,71
0,8687

0,3
0,7
0,8813

0,31
0,69
0,8932

0,32
0,68
0,9044

0,33
0,67
0,9149

0,34
0,66
0,9248

0,35
0,65
0,9341

0,36
0,64
0,9427

0,37
0,63
0,9507

0,38
0,62
0,9580

0,39
0,61
0,9648

0,4
0,6
0,9710

0,41
0,59
0,9765

0,42
0,58
0,9815

0,43
0,57
0,9858

0,44
0,56
0,9896

0,45
0,55
0,9928

0,46
0,54
0,9954

0,47
0,53
0,9974

0,48
0,52
0,9988

0,49
0,51
0,9997

0,5
0,5
1,0000

0,51
0,49
0,9997

0,52
0,48
0,9988

0,53
0,47
0,9974

0,54
0,46
0,9954

0,55
0,45
0,9928

0,56
0,44
0,9896

0,57
0,43
0,9858

0,58
0,42
0,9815

0,59
0,41
0,9765

0,6
0,4
0,9710

0,61
0,39
0,9648

0,62
0,38
0,9580

0,63
0,37
0,9507

0,64
0,36
0,9427

0,65
0,35
0,9341

0,66
0,34
0,9248

0,67
0,33
0,9149

0,68
0,32
0,9044

0,69
0,31
0,8932

0,7
0,3
0,8813

0,71
0,29
0,8687

0,72
0,28
0,8555

0,73
0,27
0,8415

0,74
0,26
0,8267

0,75
0,25
0,8113

0,76
0,24
0,7950

0,77
0,23
0,7780

0,78
0,22
0,7602

0,79
0,21
0,7415

0,8
0,2
0,7219

0,81
0,19
0,7015

0,82
0,18
0,6801

0,83
0,17
0,6577

0,84
0,16
0,6343

0,85
0,15
0,6098

0,86
0,14
0,5842

0,87
0,13
0,5574

0,88
0,12
0,5294

0,89
0,11
0,4999

0,9
0,1
0,4690

0,91
0,09
0,4365

0,92
0,08
0,4022

0,93
0,07
0,3659

0,94
0,06
0,3274

0,95
0,05
0,2864

0,96
0,04
0,2423

0,97
0,03
0,1944

0,98
0,02
0,1414

0,99
0,01
0,0808





Максимальное значение энтропии = 1

Задание 3: Пользуясь таблицей частот русского языка определить энтропию одной буквы русского текста.


Буква
Вероятность
Буква
Вероятность
Буква
Вероятность
Буква
Вероятность

Пробел
0,175
р
0,040
я
0,018
х
0,009

о
0,090
в
0,038
ы
0,016
ж
0,007

е
0,072
л
0,035
з
0,016
ю
0,006

а
0,062
к
0,028
ъ
0,014
ш
0,006

и
0,062
м
0,026
б
0,014
ц
0,004

н
0,053
д
0,025
г
0,013
щ
0,003

т
0,053
п
0,023
ч
0,012
э
0,003

с
0,045
у
0,021
й
0,010
ф
0,001

Для вычисления энтропии вводят специальную функцию: .

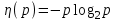Тогда формула энтропии примет следующий вид:

.

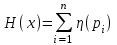Энтропии одной буквы русского текста: Н(х)= 4,348970751
Задание 4: Пользуясь заданным текстовым файлом, определить частоту появления символов в тексте. Определить энтропию одной буквы заданного текста.

Текст:

И труд нелеп и бестолкова праздность

И с плеч долой всё та же голова

Когда приходит бешеная ясность

Насилуя притихшие слова

(25 символов)

Таблица частот
 
Вероятность
Энтропия

Символ
Встречается, раз
Частота, %
Н(х)

о
11
0,106796
0,344638

и
9
0,087379
0,307274

е
8
0,077670
0,28633

с
8
0,077670
0,28633

а
8
0,077670
0,28633

т
7
0,067961
0,263631

л
7
0,067961
0,263631

д
5
0,048544
0,211872

н
5
0,048544
0,211872

п
5
0,048544
0,211872

р
4
0,038835
0,182

в
4
0,038835
0,182

я
3
0,029126
0,148588

у
2
0,019417
0,110417

б
2
0,019417
0,110417

к
2
0,019417
0,110417

ь
2
0,019417
0,110417

г
2
0,019417
0,110417

х
2
0,019417
0,110417

ш
2
0,019417
0,110417

з
1
0,009709
0,064917

ч
1
0,009709
0,064917

й
1
0,009709
0,064917

ё
1
0,009709
0,064917

ж
1
0,009709
0,064917


Энтропия H(x) равна 4,283880618.

Смотрите также файлы