ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Временные характеристики
Динамические свойства звеньев и систем определяются с помощью временных и частотных характеристик.
Временные характеристики показывают изменение во времени выходного сигнала исследуемого звена или системы при подаче на их вход типового входного сигнала. Другими словами, временные характеристики есть реакция звена или системы на входные воздействия. Различают следующие временные характеристики:
1) Переходную функцию (характеристику), обозначается, как - h(t).
2) Импульсную переходную или весовую функцию -
(t) При решении большинства задач теории автоматического управления используется математическое описание звеньев и систем в виде дифференциальных уравнений или в виде передаточных функции.
Пусть имеем звено или систему представленные в следующем графическом изображении:
W(S)
х(t) y(t)
X(S) Y(S) Где х(t), y(t) – соответственно входная и выходная величины (функции времени);
X(S) и Y(S) изображение этих величин по Лапласу.
Связь между временными функциями звена или системы х(t) и y(t) описывается дифференциальными уравнениями, которые в компактной операторной форме имеют вид: D(р) * y(t) = K(р) * х(t), где
K(р) и D(р) – полиномы правой и левой частей дифференциального уравнения звена или системы. Отношение изображения по Лапласу выходной величины звена или системы к входной называется передаточной функцией:
– передаточная функция звена или системы.K(S) и D(S) – соответственно, изображение по Лапласу полиномов правой и левой частей дифференциального уравнения звена или системы.
Если входной сигнал x(t) = 1(t) – т.е. единичная ступенчатая функция, то выходной сигнал y(t) = h(t), то естьпредставляет собойпереходную функцию.
h(t) – реакция звена или системы на единичное ступенчатое воздействие на входе при нулевых начальных условиях (
т.е. при t < 0 y(t) = 0).
Свойства и графическое представление единичной ступенчатой функции:
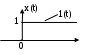
t
Используя понятие передаточной функции и преобразование Лапласа, определим h(t):
Y(S) = X(S)*W(S) – изображение выходной величины по Лапласу.
Так как x(t) = 1(t), то X(S) = L[x(t)] = L[1(t)] = 1/S, тогда
h(t) = y(t) = L-1[Y(S)] = L-1[W(S)*1/S] = L-1[W(S)/S].
Здесь L[x(t)] иL-1[Y(S)] соответственно, прямое и обратное преобразование Лапласа, т.е. переход от функции времени x(t) к изображению этой функции по Лапласу (X(S)) и наоборот отY(S) кy(t).
Если передаточная функция, исследуемого звена или системы имеет только простые и ненулевые полюса (корни характеристического уравнения D(S) = 0), то:
– формула Хевисайда, где:К(0) – полином числителя передаточной функции, при S = 0;
D(0) – полином знаменателя передаточной функции, при S = 0;
K(Si) – полином числителя передаточной функции, при S = Si;
Si – i – ый корень характеристического уравнения;
n – число корней характеристического уравнения;
D`(Si) – производная полинома знаменателя, при i- том значении корня:
при S = Si.
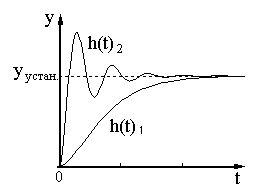
В общем случае h(t) устойчивой системы или звена имеет вид функции стремящейся к установившемуся значению (yустан.) при нулевых начальных значениях.
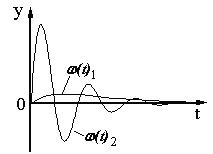
Характер устойчивого переходного процесса (монотонный h(t)1 или колебательный h(t)2, как показано на рисунке) определяется корнями характеристического уравнения исследуемого объекта: монотонный - при отрицательных действительных корнях, колебательный – при комплексных корнях с отрицательной вещественной частью.
Если корни действительные положительные - процесс, расходящийся монотонный (h(t) монотонно возрастающая функция), если корни комплексные с положительной вещественной частью – процесс расходящийся колебательный.
Импульсная переходная (весовая) функция ω(t) — есть реакция звена или системы на единичную импульсную функцию при нулевых начальных условиях.
Если х(t) = δ(t), то y(t) = ω(t). Здесь δ(t) = 1`(t) – единичная импульсная функция, есть производная от единичной ступенчатой функции.
Свойства единичной импульсной функции:
, при этом 
Г
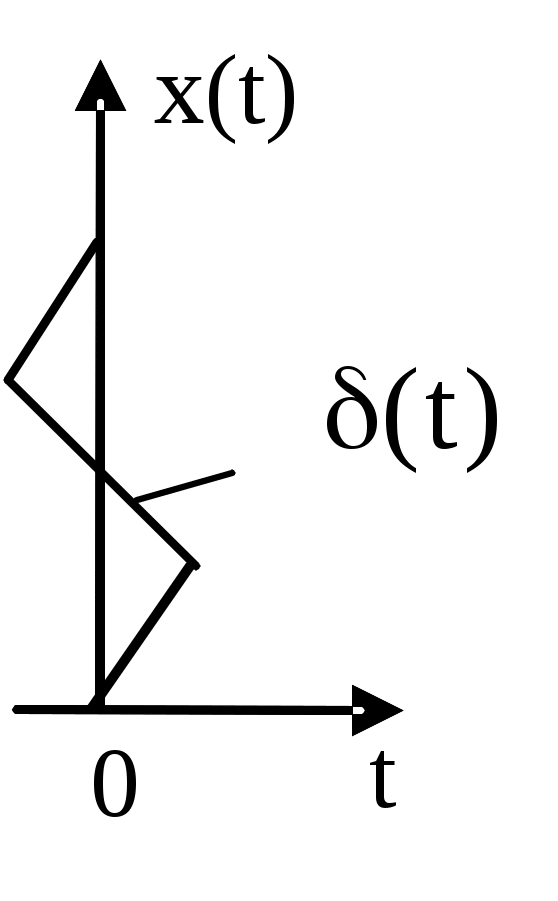рафическое представление единичной импульсной функции показано на рисунке.Реально, единичная импульсная функция представляет собой импульс при t = 0 очень малой длительности с амплитудой равной
. Площадь такого импульса равна:S= *1/ = 1 .
Аналогично определению h(t) запишем:
(t) = L-1[Y(S)] = L-1[X(S) W(S)] при х(t) = δ(t) = 1`(t).
Так как:
X(S) = L[x(t)] = L[σ(t)] = 1, получим: (t) = L-1[W(S)].
Если корни (полюса) передаточной функции простые и ненулевые, то по формуле Хевисайда имеем:
Если корни простые и ненулевые, то (t) = h`(t)Импульсная переходная (весовая) функция устойчивых процессов при t стремится к нулю. Характер изменения функции (t) (монотонный (t)1 или колебательный (t)2), как и для h(t), зависит от корней характеристического уравнения.
Характеристики (t) и h(t) – имеют одинаковую информативность, но на практике чаще используют h(t) , так как её легче получить экспериментально.Пример построения h(t) и (t) с использованием формулы Хевисайда:
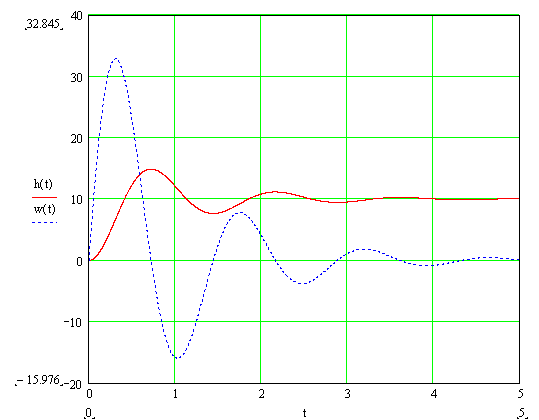
Переходная h(t) и весовая (t) функции имеют колебательный сходящийся характер, так как корни характеристического уравнения передаточной функции комплексные с отрицательной вещественной частью (s1 = -1+ i 4,359, s2 = -1- i 4,359).