РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ПЛОСКОЙ РАМЫ
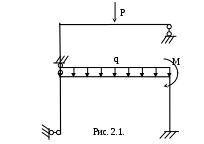
2.1. Условия задачи
Плоская рама изготовлена из стальных балок двутаврового профиля. Рама нагружена в соответствии с заданной расчетной схемой рис 2.1. Жесткость на изгиб поперечного сечения горизонтальных стержней равна EI, вертикальных – 2EI. Допускаемое напряжение , модуль упругости .

Требуется:

1. 
   раскрыв статическую неопределимость по методу сил, построить эпюры внутренних силовых факторов;
   
2. 
   обосновать правильность раскрытия статической неопределимости рамы статической и кинематической проверками;
   
3. 
   подобрать двутавровый профиль по ГОСТ 8239-72, сохранив заданное соотношение жесткостей
   
4. 
   определить угол поворота сечения 3⁴;
   
5. 
   

   M/qa2	P/qa	q, кН/м	a, м
   2,0	2,0	10,0	2,0

   исследовать напряженное состояние рамы при повреждении каждой из шарнирных опор.
   

2.2. Построение эпюр внутренних силовых факторов
Строим эквивалентную схему.

Степень статической неопределимости N_X=6-3=3. Выбираем основную систему, отбрасывая три лишние связи - шарнирные опоры. Загружаем основную систему внешними нагрузками и лишними неизвестными Х₁, Х₂ и Х_3, действующими в направлении отброшенных связей (рис. 2.2.). Эта схема, дополненная системой канонических уравнений метода сил

, где .


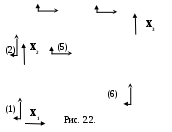
(3)

(4)


и будет эквивалентной системой. На схеме (рис 2.2.) показаны номера силовых участков (цифры в кружках), а также направления осей системы координат для каждого силового участка. Результаты сводим в таблицу 2.3. Для вычисления коэффициентов

---

системы канонических уравнений строим эпюры

Номер участка	EI(n)/EI	l(n)/a	q(n)/q
1	2	1	0
2	2	1	0
3	1	1	0
4	1	1	0
5	1	2	-1
6	2	1	0

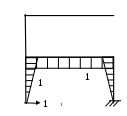
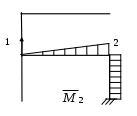
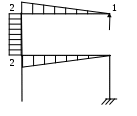
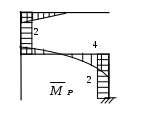
Рис. 2.3.


Результаты построения эпюр

Номер участка	M1(n)/a		M2(n)/a		M3(n)/a		MP(n)/qa2
	M0	M1	M0	M1	M0	M1	M0	M1
1	0	-1	0	0	0	0	0	0
2	0	0	0	0	2	2	-2	-2
3	0	0	0	0	2	1	-2	0
4	0	0	0	0	1	0	0	0
5	-1	-1	0	2	-2	0	2	-4
6	0	1	-2	-2	0	0	2	2

---

Коэффициенты системы канонических уравнений вычисляем по формулам:



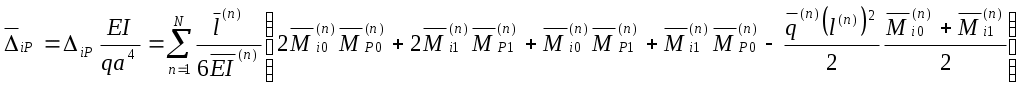или их частным случаям.

Здесь . При этом значения параметров М₀ и М₁ в начале и конце силового участка соответственно берем по табл. 2.4, а значения безразмерных параметров длины , жесткости на изгиб и безразмерной нагрузки - по табл. 2.3.





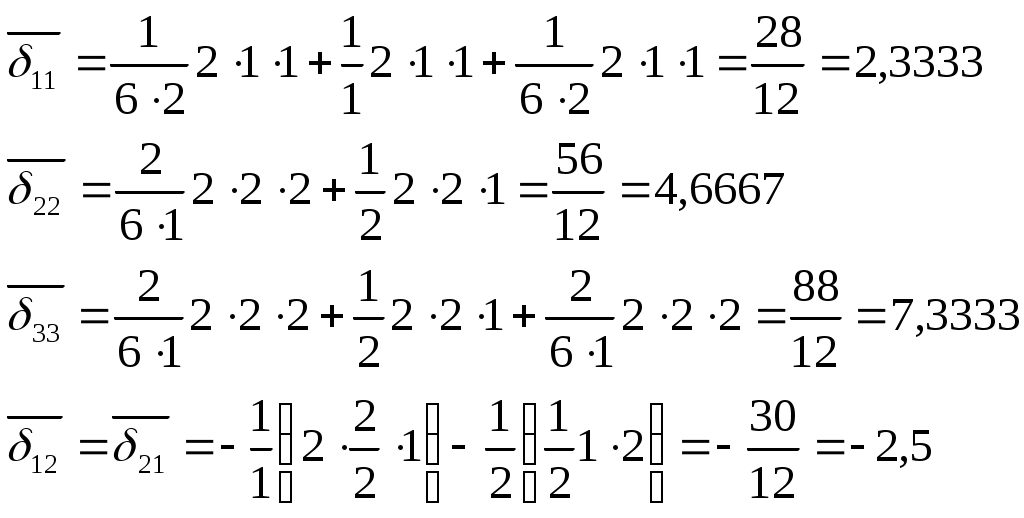
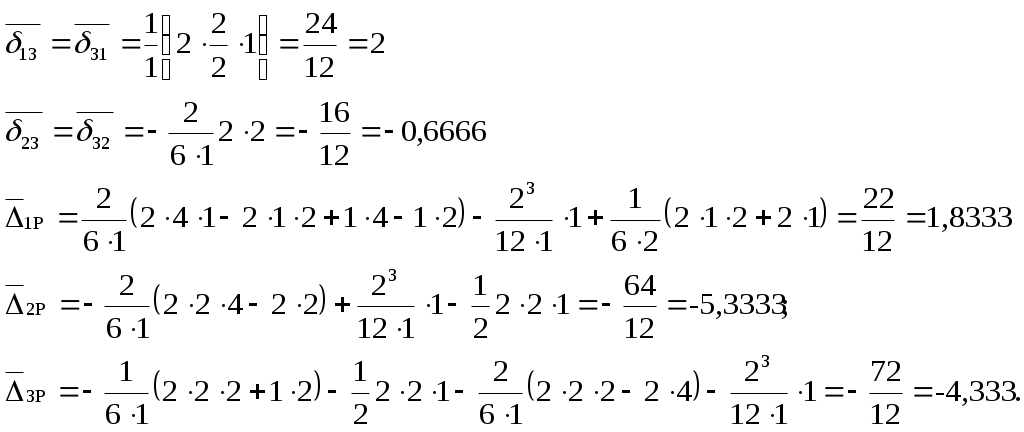
Вводя безразмерные неизвестные и умножая все коэффициенты на общий знаменатель 12, запишем расширенную матрицу системы уравнений в виде



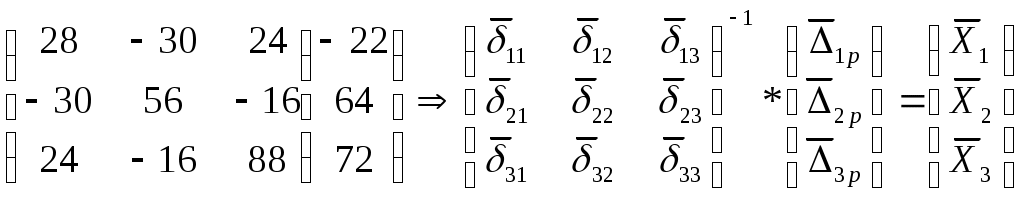
Решая эту систему, получим




1,172






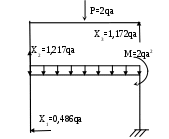
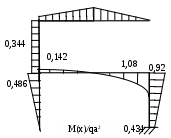
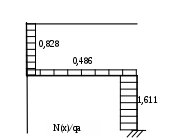
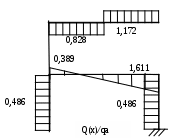
Рис. 2.4.


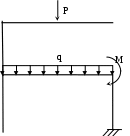
Используя полученные значения, строим эпюры внутренних силовых факторов(рис. 2.4). При построении эпюры M(x) используем формулу:

.

2.3. Обоснование правильности раскрытия статической неопределимости рамы статической и кинематической проверками
Для статической проверки рассмотрим равновесие узлов расчетной схемы (сечений, где стыкуются силовые участки балки). Из рис. 2.5 следует, что узлы расчетной схемы находятся в равновесии.

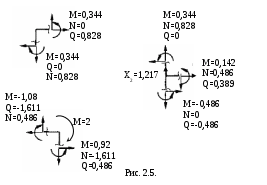
Для выполнения кинематической проверки умножим эпюру M(x) (см. рис. 2.4) последовательно на эпюры от единичных сил (рис. 2.3), найдя тем самым перемещения в направлении этих сил. По смыслу метода сил эти перемещения должны быть равны нулю.

---

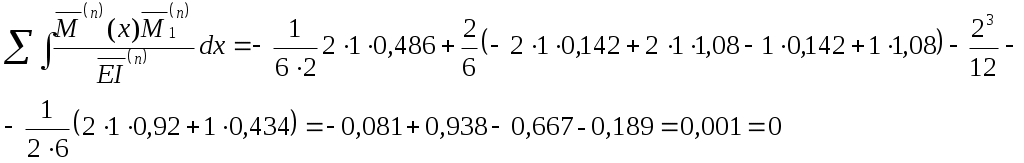
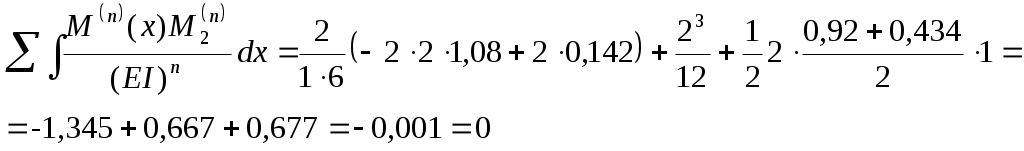
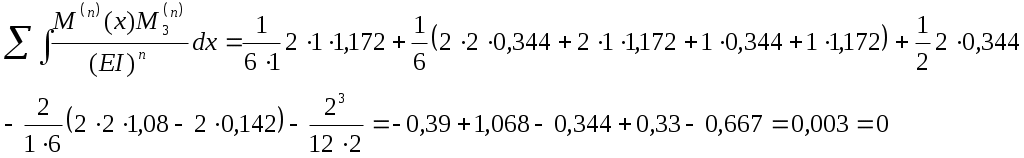
Как видим, найденные интегралы Мора с точностью вычислений равны нулю, следовательно, система (рис. 2.4) является эквивалентной заданной (рис. 2.2).
2.4. Подбор двутаврового профиля по ГОСТ 8239-72
Для обеспечения заданного соотношения жесткостей принимаем, что горизонтальные стержни выполнены из профиля двутаврового сечения с , а вертикальные – из двух таких профилей, так что . Тогда должны выполнятся соотношения:



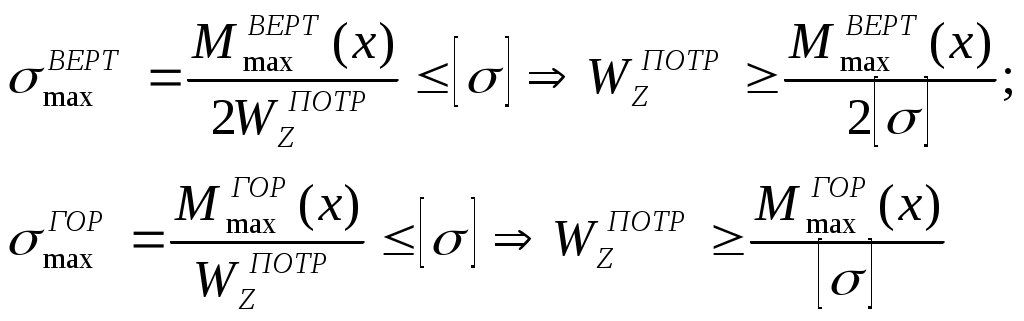
Подставляя в (2.2) значения М(х) из эпюры (рис 2.4) и учитывая заданные значения , получаем



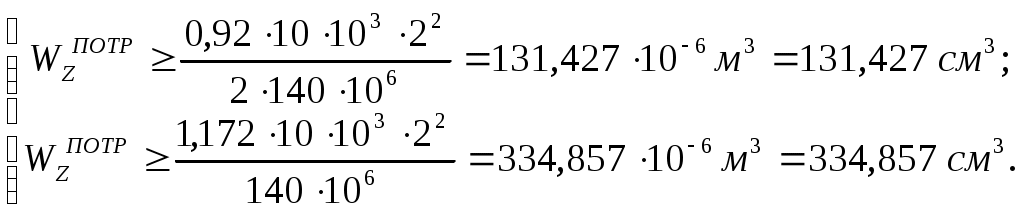
Из двух значений (2.3) выбираем наибольшее соответствующее условию прочности на вертикальных стержнях. По ГОСТ 8239-72 выбираем двутавровую балку № 27 с . При этом максимальные напряжения в раме будут составлять

.
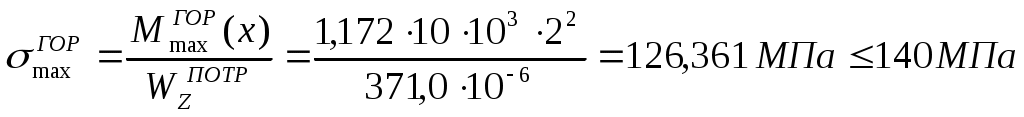2.5. Определение угла поворота заданного сечения
Для определения угла поворота сечения в точке 3 приложим в этой точке единичный момент и построим эпюру М₁^* для основной системы (рис. 2.6).

П
1
еремножая эпюры М₁^* и М(х) согласно рис.2.5. получаем

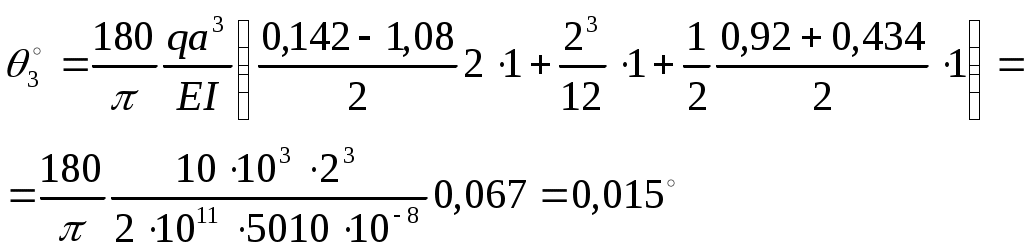
Так как в результате расчета получили положительное значение , то направление угла поворота сечения в точке 3 совпадает с направлением единичного момента на рис 2.6.

---

2.6. Исследование напряженного состояния рамы в случае повреждения опор
В процессе работы конструкции одна из опор может быть повреждена. Так как система является статически неопределимой, работоспособность конструкции будет сохранена, но при этом напряжения в раме перераспределятся и при заданном значении q могут превысить допускаемые.

Для оценки возможности работы рамы при повреждении, например, шарнирной опоры в точке 2, следует положить неизвестное Х₂=0 и вместо матрицы (2.1.) рассматривать матрицу

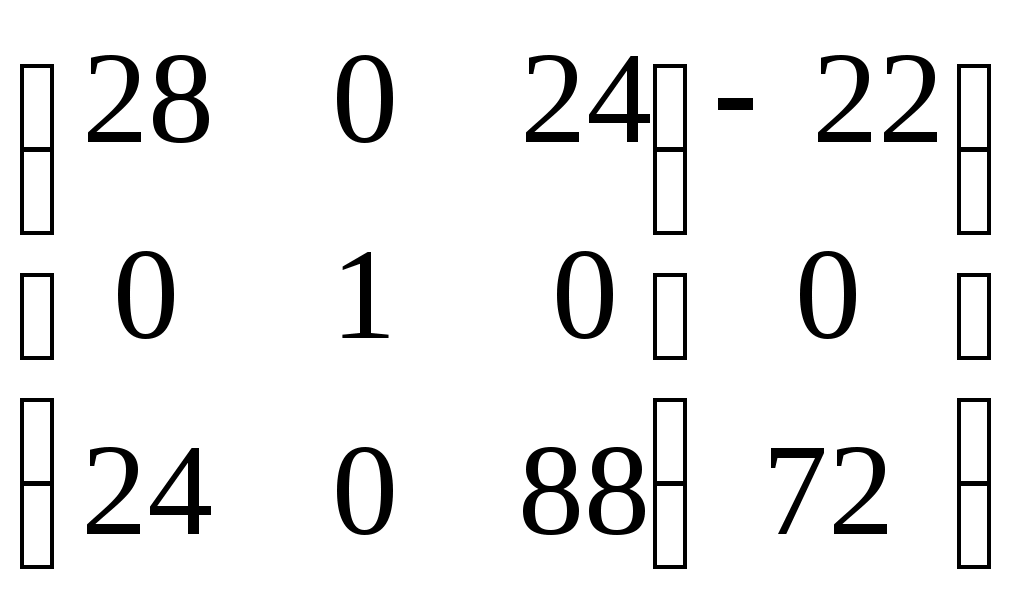(2.4.)

Решая (2.4), получаем



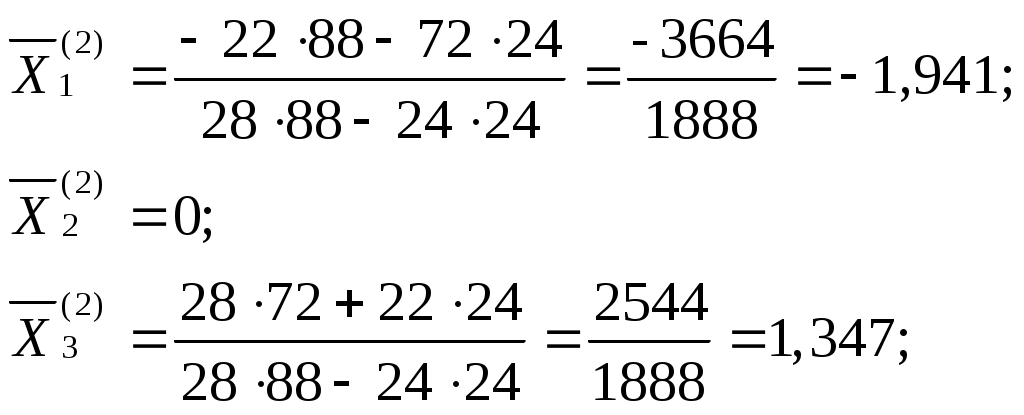
Здесь верхний индекс у X_i указывает на номер поврежденной опоры.

Аналогично считаем два других случая.

Далее следует построить эпюру M(x) и рассчитать напряжения в поврежденной конструкции.

Результаты расчетов показаны на рис 2.7 в виде эпюр изгибных напряжений, которые подсчитывались по формуле .

Из графиков видно что при повреждении опоры 2 максимальные напряжения составляют 221,994 МПа, что в 221,994/140=1,585 раза превышает допускаемые напряжения. Следовательно, для безопасной эксплуатации поврежденной конструкции необходимо во столько же снизить эксплуатационную нагрузку. При этом она будет [q]⁽²⁾=10/1,585=6,306 кН/м

Аналогичные результаты получаются и при повреждении опоры 3. максимальные напряжения 215,633 МПа в 215,633/140=1,54 раза превышают допускаемые. Поэтому допускаемая эксплуатационная нагрузка будет [q]⁽³⁾=10/1,54=6,492 кН/м

Иная картина наблюдается при повреждении опоры 1. В этом случае максимальные напряжения 118,167 МПа ниже допускаемых.

Т
8,841 9703504043126684636118598383138,408
аким образом, если позволяют конструктивные особенности, эту опору желательно убрать.
32,095



Повреждена опора 1

Неповрежденная конструкция


Повреждена опора 2

Повреждена опора 3

Рис. 2.7 Эпюры поврежденных конструкций

---

Смотрите также файлы

• 1. Кариотип это .pdf

• национальный исследовательский томский политехнический университет юргинский технологический институт.pdf

• Макроэлемент Кремний (Si) для чего нужен, в каких продуктах содержится.docx

• Литература (с нерусским языком обучения) 9 класс.doc

• Обособление.ppt